InterviewSolution
Saved Bookmarks
| 1. |
What is the value of 6t such that volume contained inside the planes sqrt(1-t^(2))x+tz=2sqrt(1-t^(2)), z=0,x=2+(tsqrt(4t^(2)-5t+2))/(sqrt(12(1-t^(2))^(1//4))) and |y|=2 is maximum. |
|
Answer» When we cut these planes by the plane `y=0`, the triangle OBTAINED is `ABC`, where `AB=(tsqrt(4t^(2)-5+2))/(SQRT(12)(1-t^(2))^(1//4))` LET `CAB=theta=` angle between first and `xy` plane, the `costheta=t` 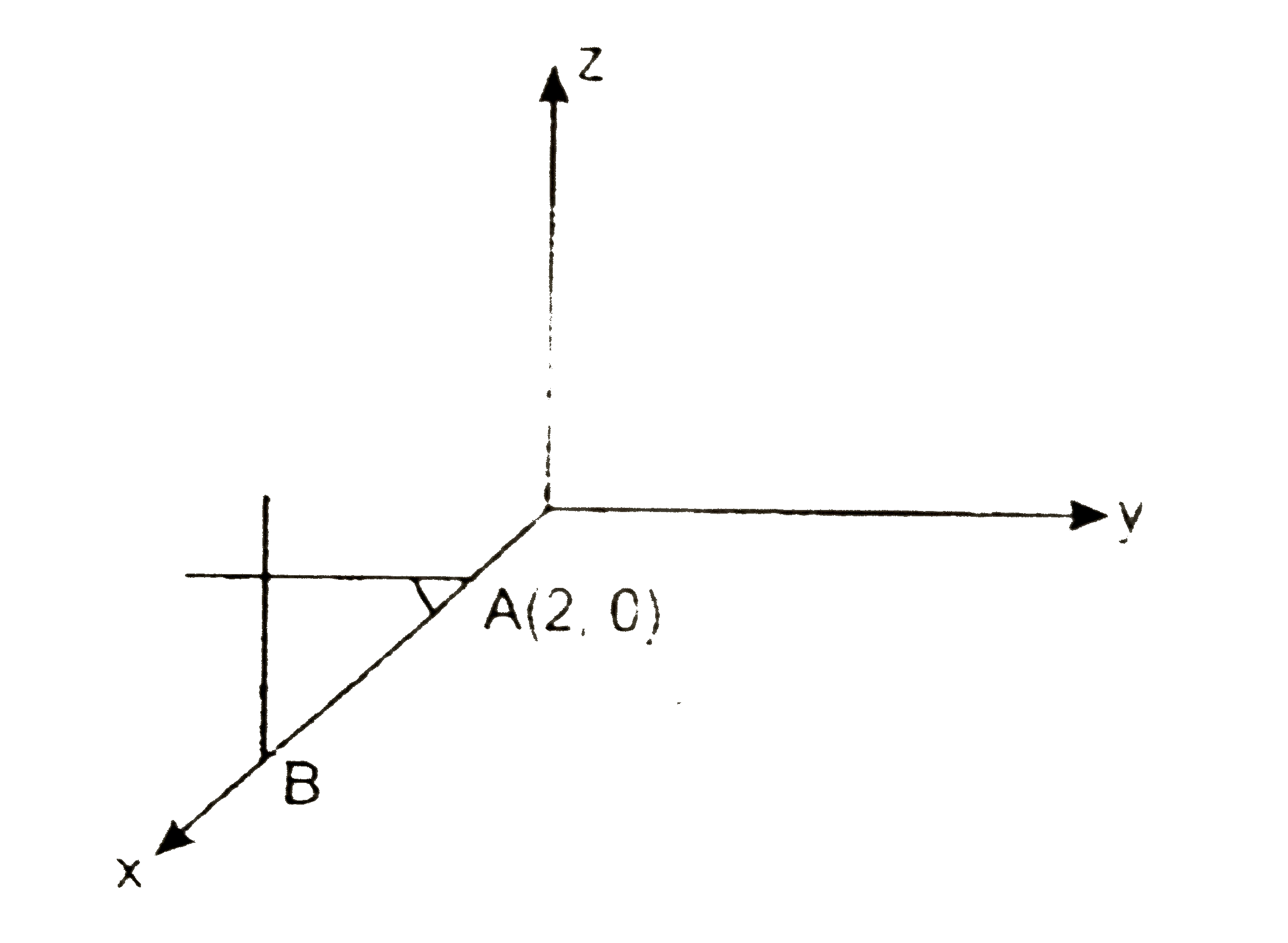 Area of `DeltaABC=Delta=1/2(AB)^(2)tantheta` `Delta=1/2(t^(2)(4t^(2)-5t+2))/(12(1-t^(2))^(1/2))XX(sqrt(1-t^(2)))/t=1/2 (4t^(3)-5t^(2)+2t)/12` For example `(dDelta)/(dt)=0implies12t^(2)-10t+2=0` `impliest=(10+-sqrt(100-96))/24=1/2` or `1/3` Now, `(d^(2)Delta)/(dt^(2))=24t-10` So, `Delta`"is maximum at"`t=1/3`"and minimum at "`t=1/2` `:. t=1/3` |
|