InterviewSolution
Saved Bookmarks
| 1. |
Write a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept. |
|
Answer» Solution :`*` Since g has vertical is asymptotes x = 3 and x = -3, then the denominatorof the rational function contains theproduct of (x-3) and (x+3) . Function g has the form `g(x)=(H(x))/((x-3)(x+3)` `*` For the horizontal asymptote to EXIST, the numerator h(x) of g(x) has same DEGREE as that of the denominator with a leading COEFFICIENT equal to -4. At the same time, h(x) has no REAL zeros. Hence `f(x)=(-4x^(2)-6)/((x-3)(x+3))` `*` Check the characteristics in the graph of g shown below. 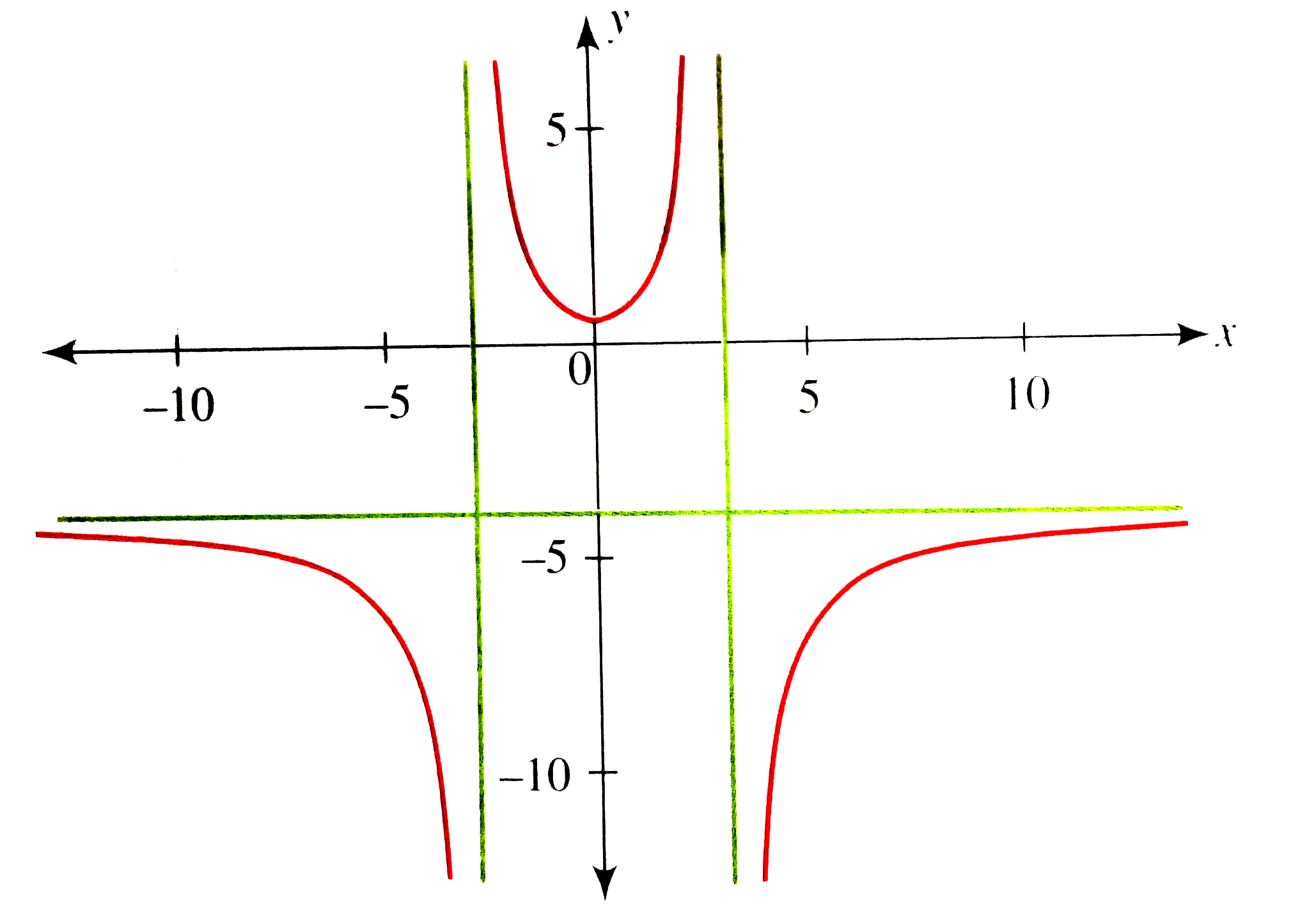
|
|