InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
""^(64)Cu(T""_(50)=12.8 year) decays beta-emission (38%), beta""^(+) decayproducts and calculate partial half-lives for each of the decay process. |
|
Answer» Solution :`""_(29)Cu""^(64)` UNDERGOES (i) `B""^(-)` emission (ii) `B""^(+)` emission (iii) electron capture 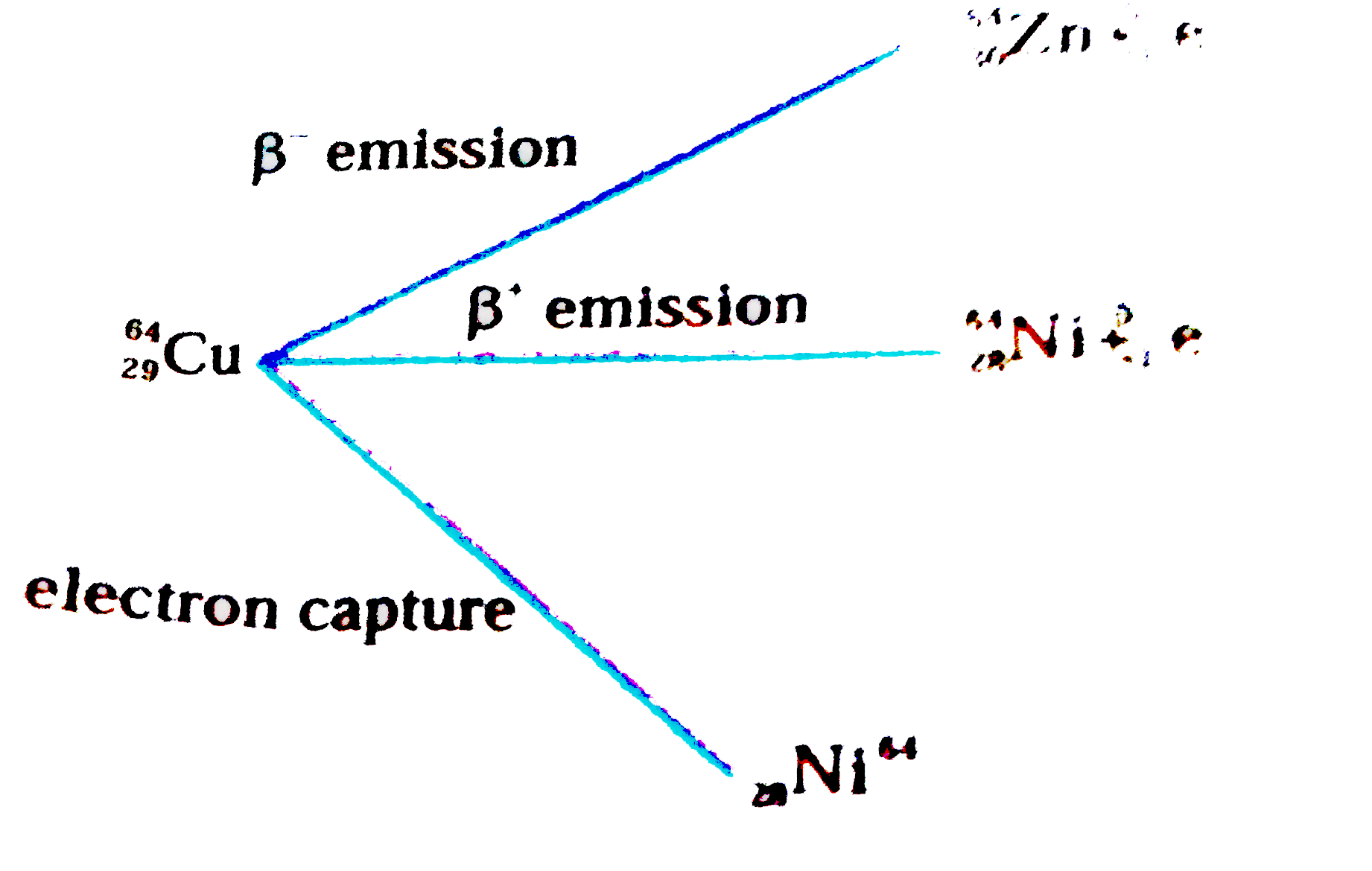 Let the rate CONSTANT for `beta ""^(-)` emission = `K""_(1)` Let the rate constant for `beta""^(+)`emission = `k""_(3)` Let the rate constant for electron capture emission = `k""_(3)` Overall rate constant `K=K""_(1)+K""_(2)+K""_(3)=(0.693)/(t""_(1//2) )=(0.693)/(12.8)H""^(-1)` `t""_(1//2)` of `""_(29)Cu""^(64)=12.8h` `K""_(1)` = % of its decay `xx` Rate constant (overall) `(38)/(100)xx k=(0.38xx0.693)/12.8h""^(-1)` `t""_(1//2)` of `beta""^(-)` emission = `(0.693)/(K)=(0.693xx12.8)/(0.38xx0.693)` `=(12.8)/(0.38)` (partial half life) = 33.68 hr. `K""_(2)` = % of `beta""^(oplus)` decay `xxK` (overall) `=(19)/(10)xx(0.693)/(12.8)xx(0.19xx0.693)/(12.8)h""^(-1)` Let `(t""_(2))""_(1//2)` be the half life of `beta""^oplus` emission `=(0.693)/(K""_(2))=(0.693xx12.8)/(0.693xx0.19)=(12.8)/(0.19)` = 67.37 hr |
|