1.

A block is dragged on a smooth plane with the help of a rope which moves with velocity (v) shown in Fig. 2 (CF). 25 , The horizontal velocity of the block is .

Answer» <html><body><p>`v` <br/>` v <a href="https://interviewquestions.tuteehub.com/tag/sin-1208945" style="font-weight:bold;" target="_blank" title="Click to know more about SIN">SIN</a> <a href="https://interviewquestions.tuteehub.com/tag/theta-1412757" style="font-weight:bold;" target="_blank" title="Click to know more about THETA">THETA</a> `<br/>v//sin theta`<br/>`v//cos theta`</p>Solution :<a href="https://interviewquestions.tuteehub.com/tag/let-11597" style="font-weight:bold;" target="_blank" title="Click to know more about LET">LET</a> ` AB = X, then ` <a href="https://interviewquestions.tuteehub.com/tag/ac-361271" style="font-weight:bold;" target="_blank" title="Click to know more about AC">AC</a>= x cos theta` <br/> :. ` (d(AC)/(dt) = d/(dt) (x cos theta) = (<a href="https://interviewquestions.tuteehub.com/tag/dx-960990" style="font-weight:bold;" target="_blank" title="Click to know more about DX">DX</a>)/(dt) cos theta + x (- sin theta) (d theta)/(dt)` <br/> But `(d(AC)/(dt) = 0 `, so ` 0= (dx)/(dt) cos theta + x ( - sin theta) ( d theat)/(dt)` <br/> or ` v cos theta = x sin theta = x sin theta (d theta)/(dt)` or ` (dtheta)/(dt) = ( v cos theta)/(x sin theta)` 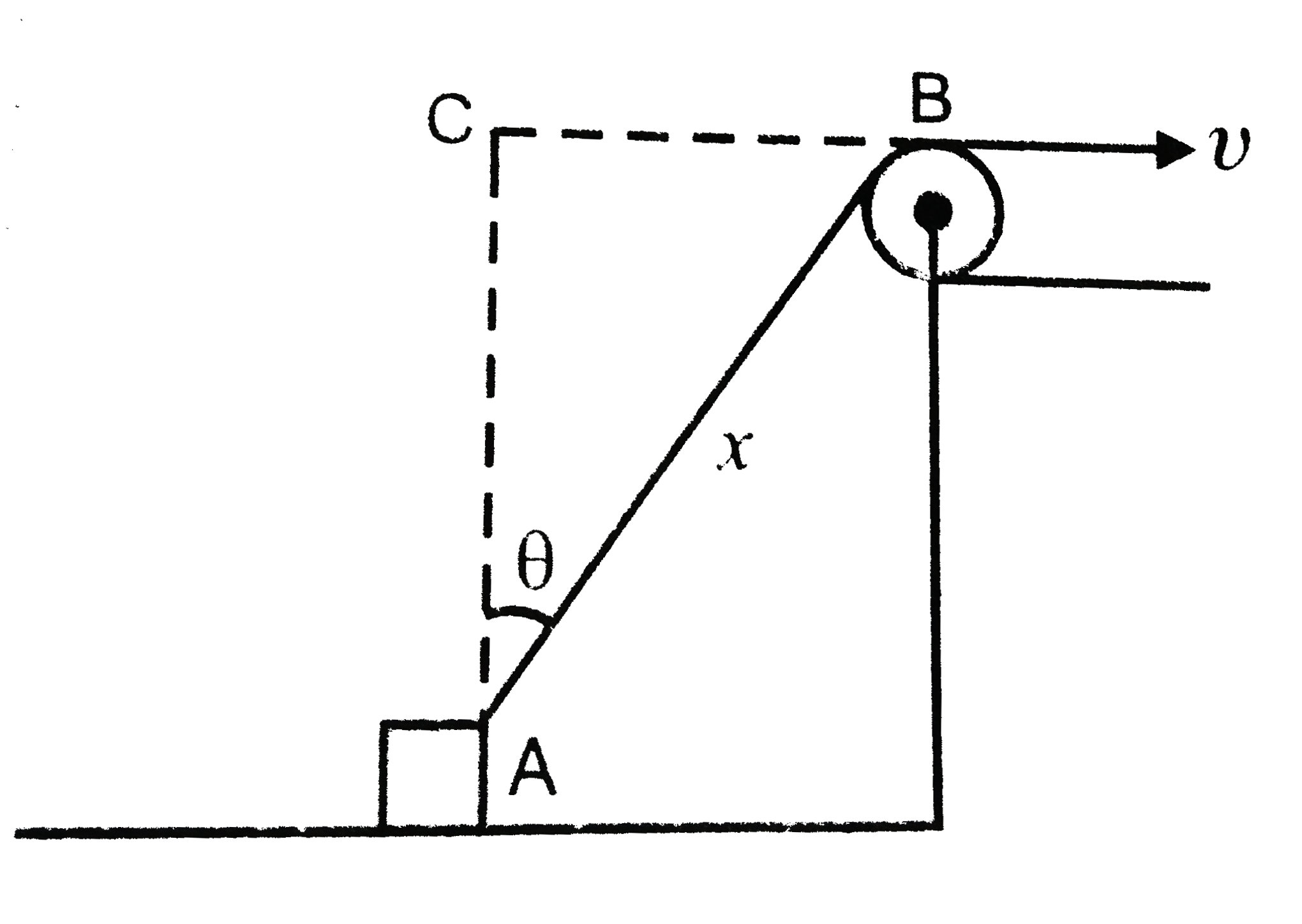<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XI_V01_C02_E01_371_S01.png" width="80%"/>. <br/> Also , ` CB = x sin theta`. <br/> Velocity of block will be <br/> ` u = sin theta + x cos theta xx (v cos theta)/( x sin theta)` <br/> ` (v (sin^@ theta + cos^2 theta)/( sin theta) = v/(sin theta)`.</body></html>


Discussion

No Comment Found

Related InterviewSolutions