Saved Bookmarks
| 1. |
A block of mass m_(1) =1kg and another mass m_(2) = 2kg are placed together(see figure) on an inclined plane with angle of inclination theta varius value of theta are given in list 1 The coefficient of friction between the block m_(1) and the plank is always zero The coefficient of static and dynamic friction between the block m_(2) and the plank are equal to mu = 0.3 In List II experssions for the friction the block m_(2) are given Match the correct experssions of the frictionless in List II with the angle given in list 1 and choice the correct option The acceleration due too gravity detented by g [Useful information tan (5.5^(@)) = 0.1 tan (11.5^(@)) = 0.2 tan (16.5^(@)) = 0.3] List I P.theta = 5^(@) Q. theta = 10^(@) R. theta = 15^(@)S. theta = 20^(@) List 2 1.m_(2)g sin theta 2.(m_(1) + m_(2))g sin theta 3.mu m_(2)g cos theta 4. mu (m_(1) + m_(2))g cos theta |
|
Answer» `P-1, Q-1,R-1,S-3` 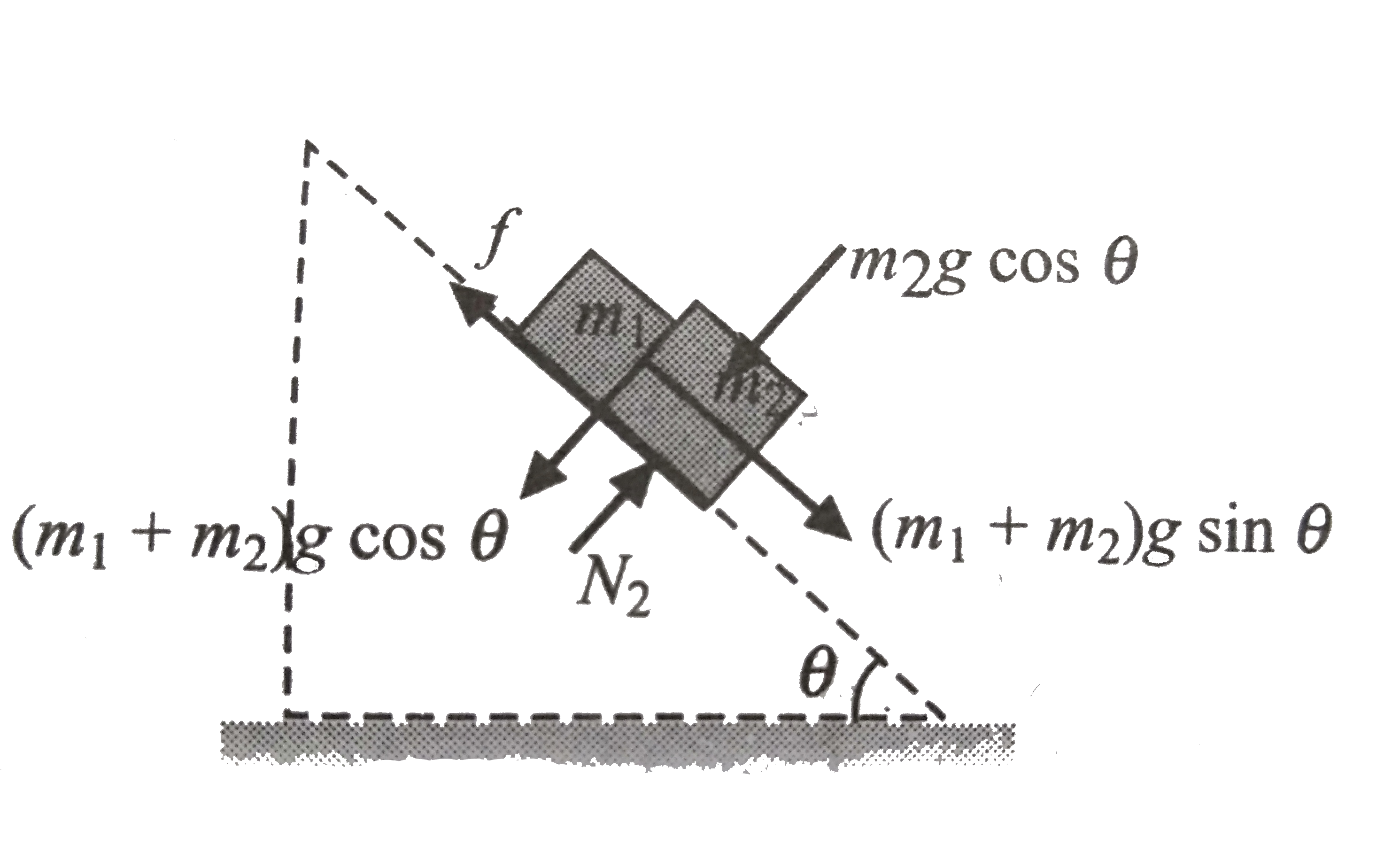 `f_(max) = (m_(1) + m_(2))g sin THETA` `mu N gt (m_(1) + m_(2))g sin theta` `0.3m_(2)g costheta ge (1+2)10 sin theta` `0.3 xx 2 xx 10 cos theta ge (1+2)10 sin theta` `6 ge 30 tan theta` `1//5 TANTHETA rArr 0.2 ge tan theta` Now it is clear in case`(P)(Q)` it will slip friction is `(m_(1)+ m_(2))g sin theta` `rArr F = (m_(1)+ m_(2))g sin theta` in the case `(R) (S)` of they slipso friction should be kinetic i.e. `mu m_(2) g cos theta` |
|