Saved Bookmarks
| 1. |
A block of mass m can slide freely in a slot made in a bigger of mass M as shown in fig. There is no friction anywhere in the system. The block m is connected to one end of a string whose other end is fixed at point P. system is released from rest when the string at P makes an angle theta with horizontal. Find the acceleration of m and M after release. |
|
Answer» Solution :Method 1: Just after the release of SYSTEM, block M will move towards left (say with acceleration A) and block m will move down with respect ot M (say with acceleration a). As there is no motion of M is vertical direction, hence the acceleration of m in verticle direction will be same as that of M, i.e. A, because horizontal both move together. Finding constraint Method 1: Let just after release, during a small time dt, the displacement of m(w.r.t. M) is dy downwards and that of M is dx horizontally asshown in fig. Decreases in the length of segment I`=underset(bar)d xcos theta` Increases in the length of segment II' `underset(bar)d y` As the total length of the string is constant , so `underset(bar)d = underset(bar)d x cos theta` ..(i) 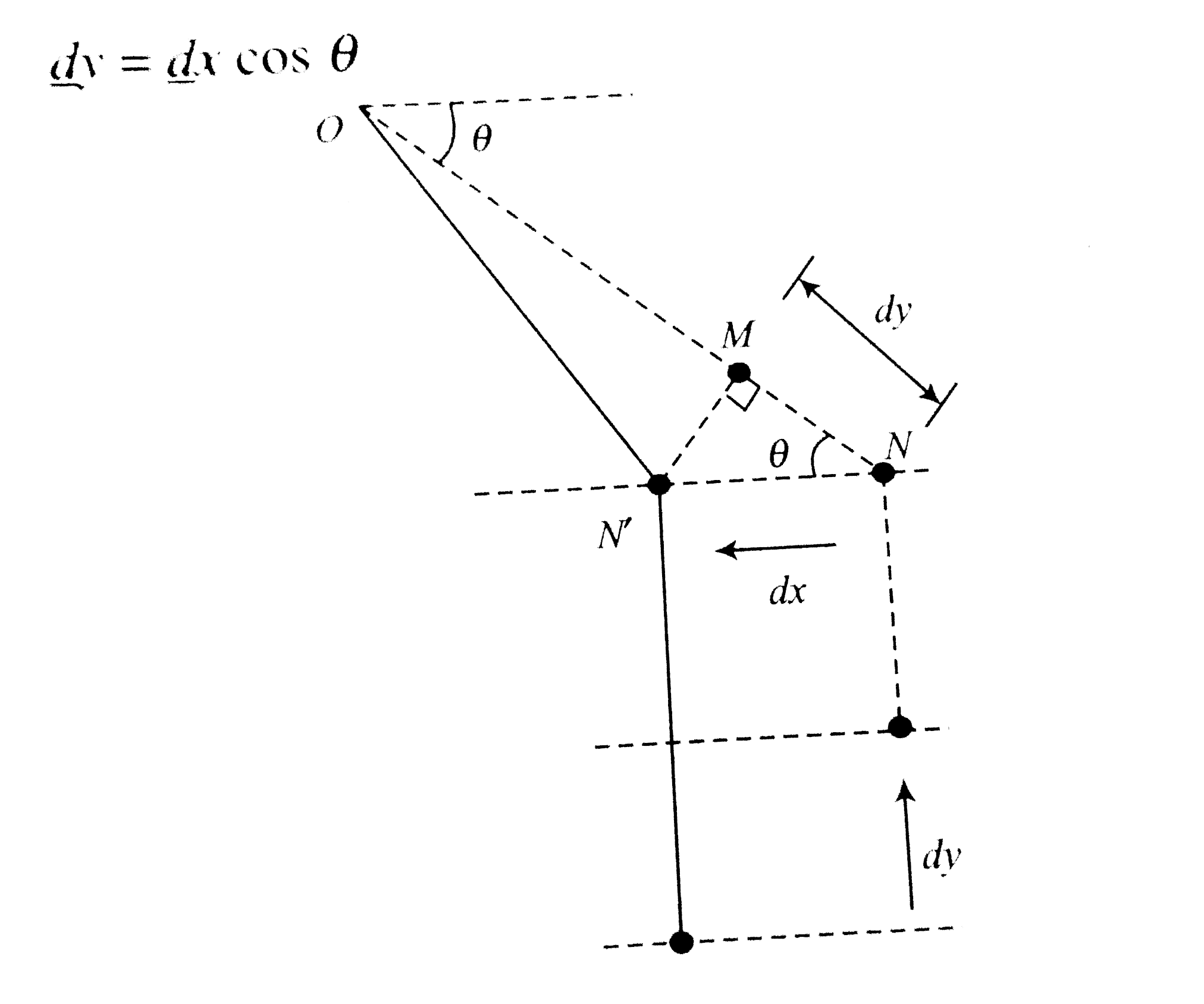 Divinding both sides by dt, we get `(dy)/(dt)=(dx)/(dt) cos theta implies v = V cos theta` ..(ii) differenting w.r.t. `t=(dv)/(dt)=V(- sin theta)(d theta)/(dt)+(dV)/(dt) cos theta` But initially `V=0`, as `a=A cos theta` ...(iii) (`:. (dv)/(dt) = a , (dV)/(dt)=A`) Method 2: we can obtain (i) in the following way. 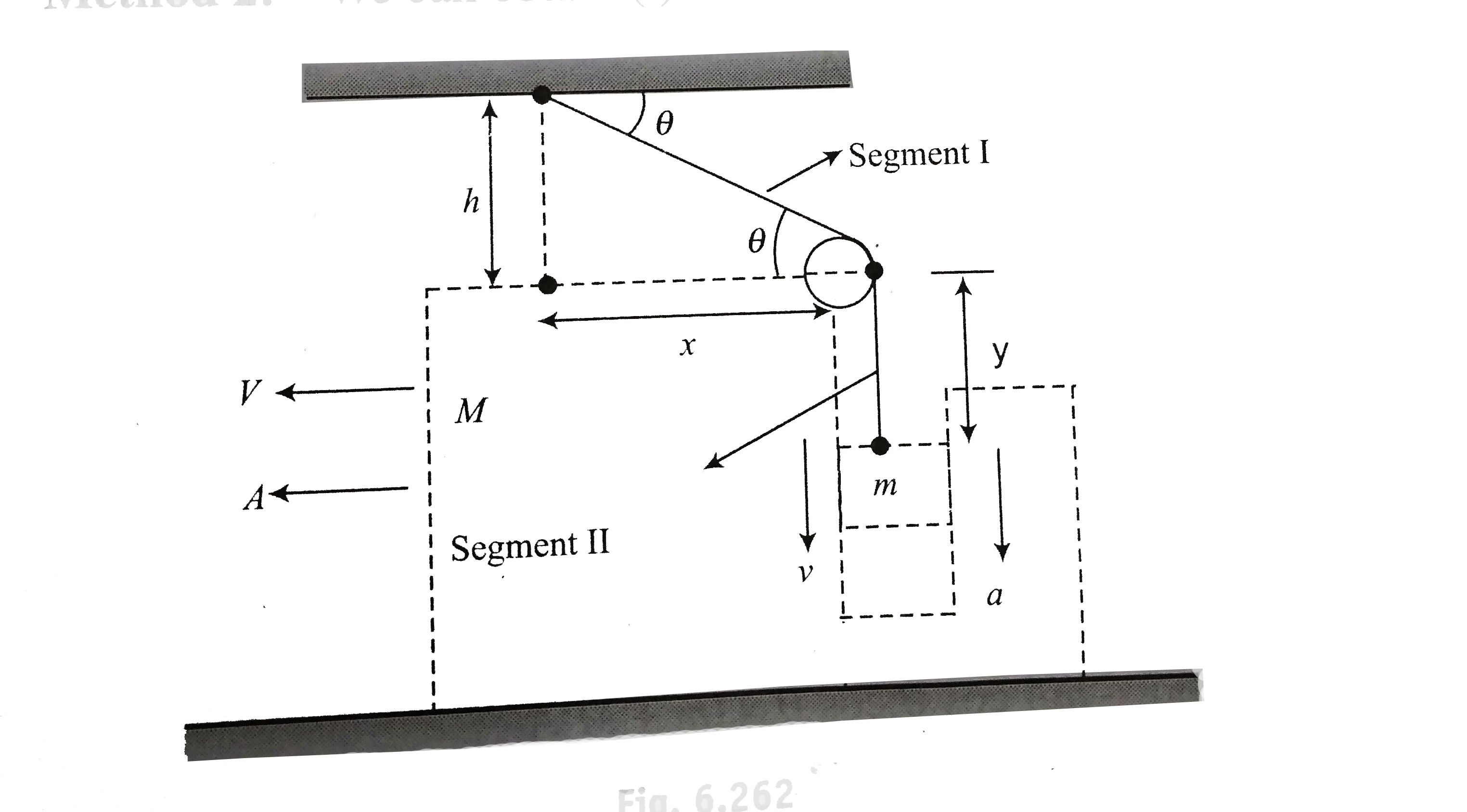 The displacment of M towards left is dx, then its component along AP is `dx cos theta`should be decreased in the length of segment I and this should be equal to increases in the length of segment II which is dy. Hence, `dy=dx cos theta`. `rArr a = A cos theta` Method 3: Total length of string : `l=sqrt(h^(2)+y^(2))+x` differentiating w.r.t. `t=(dl)/(dt) =(d(h^(2)+x^(2))^(1//2))/(dt) +(dx)/(dt)` `rArr 0=(2y(dy)/(dt))/(2sqrt(h^(2)+y^(2)))+(dx)/(dt)rArr0= cos theta (-V)+r` (`because(dx)/(dt)=v, (dy)/(dt)=-V`(as y decreases with time) and `cos theta=(y)/(sqrt(h^(2)+y^(2)))` `implies v=V cos theta` which is same as (ii) Now finding acceleration of blocks We can use any of the following method to find the value of A and a .  Method 1: From FBD of M: `T cos theta-N = MA` ...(IV) From FBD of m: `N=mA` ..(v) `MG-t=ma` ..(vi) Combining (iv) and (v) we get `T cos theta=(m+M)A`...(vii) Putting `a=A cos theta` in (iv) we get `mg-T=mA cos theta`..(viii) Put the value of T form (viii) into (vii) we get `(mg-mA cos theta)cos theta=(m+M)A` `implies A=(mg cos theta)/(M+m(1+cos^(2)theta))` and `a=A cos theta=(mg cos^(2)theta)/(M+m(1+cos^(2) theta))` The net acceleration of m is `sqrt(A^(2)+a^(2))=A sqrt(1+cos^(2) theta)=(mg cos thetasqrt(1+cos^(2) theta))/(M+m(1+cos^(2) theta))` Method 2: Analyzing the block with w.r.t. wedge  W.r.t M, m has only vertcal acceleration which is a downwards. Here we have to apply pseudo force because M is a non inertial frame. FBD of m w.r.t. M: `N=mA, mg-T=ma` These equation are same as (v) and (vi). Now solve to get answer. Method 3: Analyzing the block and wedge together Analyzing the system of `(M+m)`, i.e. , block and wedge together in horizontal direction, in horizontal direction both masses have same acceleration which is A. 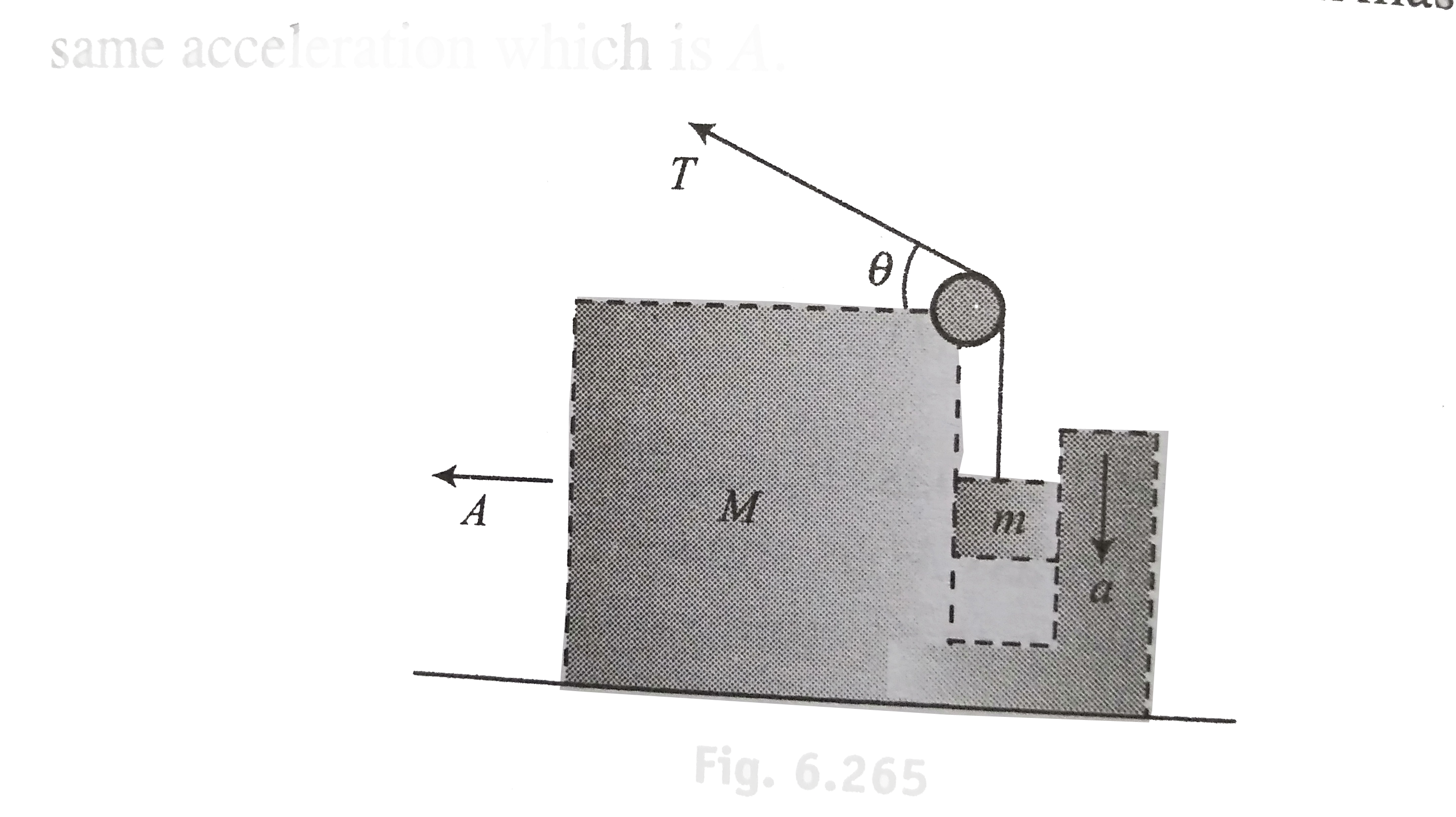 `T cos theta=(M+m)A` ...(ix) Analyzing the motion of blcok in vertical direction `mg-T=ma` ..(x)  SOLVING (ix) and (x) , we get `A=(mg cos theta)/(M+m(1+cos^(2) theta))` and `a=(mg cos^(2)theta)/(M+m(1+cos^(2) theta))` |
|