(a) CH_(3)-CH=CH-CH=CH-C_(2)H_(5) (Molecule with dissimilar ends). Here n=2, So Number of G.I = 4 [cis, cis), (trans, trans), (cis, trans,), (trans, cis)] (b) CH_(3)-CH=CH-CH=CH-CH_(3) (Molecule with similar ends) Here n=2, So Number of G.I =3 [(cis, cis), (trans, cis), (cis, trans) = (trans, cis)] (c) CH_(3)-CH=CH-CH=CH-CH=CH-CH_(3) (Molecule with similar ends) Here n=3, So Number of G.I =6 [(cis, cis, trans)= (trans, cis, cis) (cis, trans, trans) = (trans, trans, cis), (cis, cis, cis) (trans, trans, tans), (cis, trans, cis, (trans, cis, trans)] (d) Let us draw the total stereoisomers ofCH_(3)-overset(***)(underset(overset(|)(OH))(CH))-overset(***)(underset(overset(|)(OH))(CH))-overset(***)(underset(overset(|)(OH))(CH))-CH_(3) (e) Let us draw the total stereoisomers of CH_(3)-overset(***)(underset(overset(|)(OH))(CH))-overset(***)(underset(overset(|)(OH))(CH))-CH_(3) (f) Let us draw the total stereoisomers of CH_(3)-CH(OH)-CH_(2)-CH=CH-CI

(a) CH_(3)-CH=CH-CH=CH-C_(2)H_(5) (Molecule with dissimilar ends). He

1.	(a) CH_(3)-CH=CH-CH=CH-C_(2)H_(5) (Molecule with dissimilar ends). Here n=2, So Number of G.I = 4 [cis, cis), (trans, trans), (cis, trans,), (trans, cis)] (b) CH_(3)-CH=CH-CH=CH-CH_(3) (Molecule with similar ends) Here n=2, So Number of G.I =3 [(cis, cis), (trans, cis), (cis, trans) = (trans, cis)] (c) CH_(3)-CH=CH-CH=CH-CH=CH-CH_(3) (Molecule with similar ends) Here n=3, So Number of G.I =6 [(cis, cis, trans)= (trans, cis, cis) (cis, trans, trans) = (trans, trans, cis), (cis, cis, cis) (trans, trans, tans), (cis, trans, cis, (trans, cis, trans)] (d) Let us draw the total stereoisomers ofCH_(3)-overset(*)(underset(overset(\|)(OH))(CH))-overset()(underset(overset(\|)(OH))(CH))-overset()(underset(overset(\|)(OH))(CH))-CH_(3) (e) Let us draw the total stereoisomers of CH_(3)-overset()(underset(overset(\|)(OH))(CH))-overset(**)(underset(overset(\|)(OH))(CH))-CH_(3) (f) Let us draw the total stereoisomers of CH_(3)-CH(OH)-CH_(2)-CH=CH-CI
Answer» Solution :n=3 (odd CHIRAL centers with similar ends.) so, Total STEREOISOMERS `=2^(3-1) = 2^(2) = 4 ("enantlomers " = 2^(n-1) - 2^((n-1)/(2)) " & MESO compounds "=2^((n-1)/(2)))` So, total isomers `=2^(n-1) + 2^((n)/(2)-1) ("enantiomers "=2^(n-1) " & meso compounds "=2^((n)/(2)-1))` 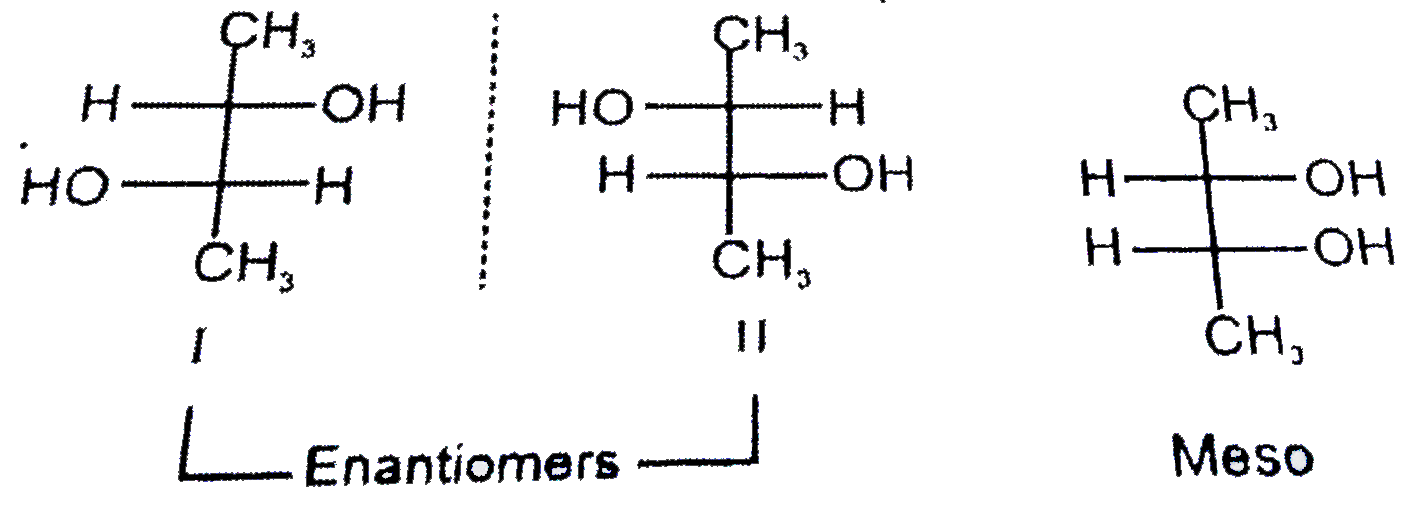Total stereo cneters (n) = 1+1 = 2 (Molecule with dissimilar ends) So, total stereoisomers`=2^(2) = 4` [(R, CIS), (R, trans), (S, cis), (S, trans)]