InterviewSolution
Saved Bookmarks
| 1. |
(a) Draw the graph of f(x) = ={{:(1",",, |x| ge 1), ((1)/(n^(2)) ",",, (1)/(n)lt |x|lt (1)/(n-1)","n= 2"," 3"," ...), (0",",, x=0):} (b) Sketch the region y le -1. (c) Sketch the region |x| lt 3. |
|
Answer» Solution :(a)`f(x) = ={{:(1",",, |x| ge 1), ((1)/(n^(2)) ",",, (1)/(n)lt |x|lt (1)/(n-1)","n= 2"," 3"," ...), (0",",, x=0):}` `""={{:(1",",, xle -1 or x ge 1), ((1)/(4) ",",, x in (-1, -(1)/(2))uu ((1)/(2), 1)), ((1)/(9) ",",, x in ((-1)/(2), (-1)/(3))uu ((1)/(3), (1)/(2))),(...,,):}` 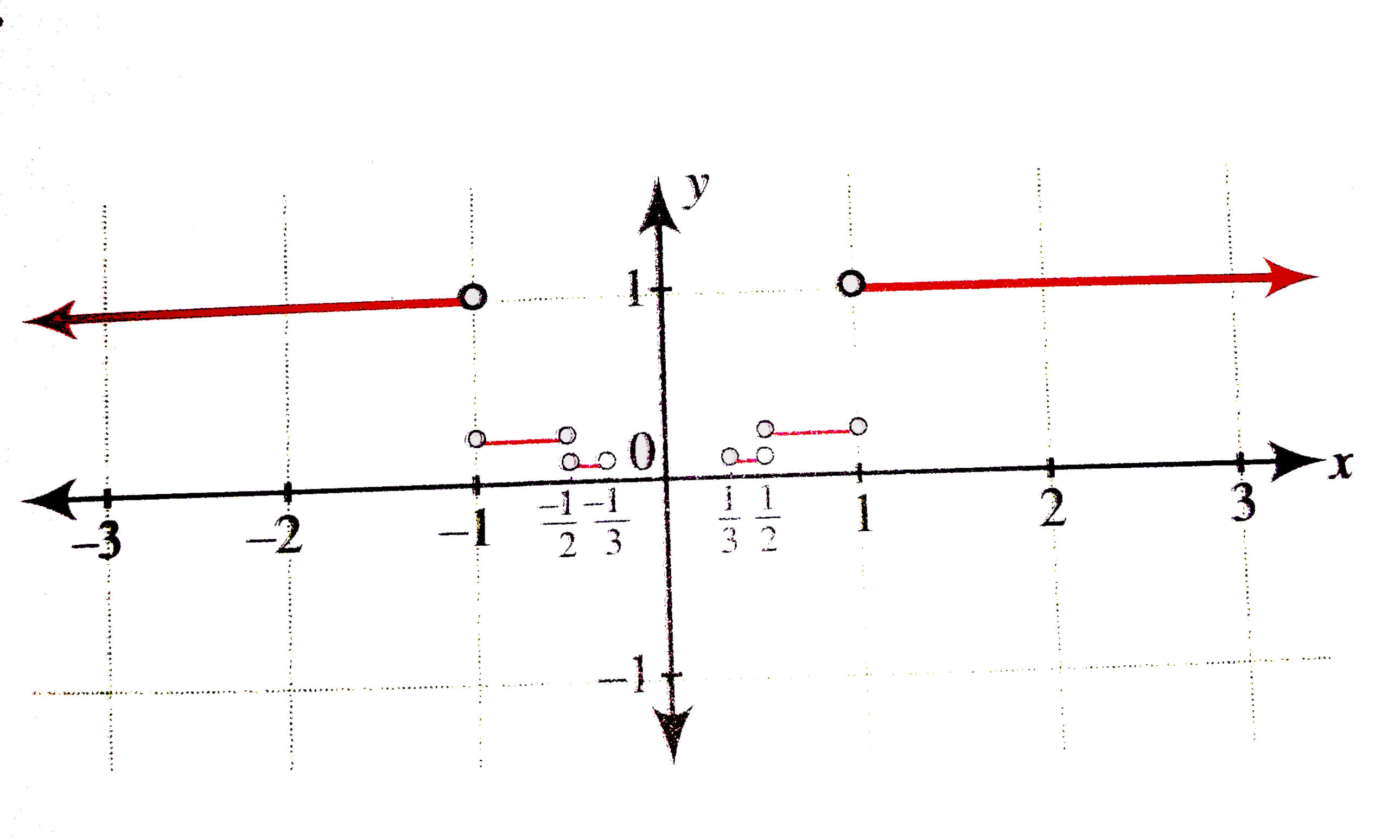 (B) `y le -1` For `y le -1`, first DRAW the line `y =-1`. All the POINTS SATISFYING `y le -1` have ordinate greater than, or equal to, -1, i.e. all the points lying on or below the line `y=-1`. The region is as shown in the following region.  (c )` |x| lt 3` So `-3 lt x lt 3`, i.e. all points have abscissae lying between -3 and 3. HENCE all the points lying between the lines `x=-3 and x=3`. 
|
|