Saved Bookmarks
| 1. |
(a) In which direction should the motorboat given in Illustration 5.46 head in order to reach a point on the opposite bank directly east from the starting point ? The boat's speed relative to the water remains 4 ms^-1. (b) What is the velocity of the boat relative to the earth ? ( c) How much time is required to cross the river ? |
|
Answer» SOLUTION :As the boat has to each exact opposite end to the point of start, the boat has to start (velocity `4 m s^-1`) at an angle `theta` aiming somewhat upstream. Taking into count the PUSH given by the current, Velocity of boat w.r.t. river, `vec v_(b,r) = vec(OA) = 4 m s^-1` Velocity of river w.r.t. Earth, `vec v_r = vec(AB) = 2 m s^-1` velocity of boat w.r.t. Earth, `vec v_b m s^-1 = vec(OB) = ?` (a) To find the direction of the boat in which the boat has to GO,we need to find angle `theta`. From `Delta OBA, sin theta = (AB)/(OA) = (2)/(4) = (1)/(2) rArr theta = 30^@` Hence, the motorboat has to head at `30^@` north of east. (b) To find the velocity of boat w.r.t. Earth, we can use pythagorous theorem again. FRO `Delta OBA`, we have `v_(b,r)^2 = v_b^2 + v_r^2 rArr v_b^2 = v_(b,r)^2 - v_r^2` `rArr v_b^2 = sqrt(v_(b,r)^2 - v_r^2) = sqrt(4^2 - 2^2) = 2 sqrt(3) m s^-1` ( c) Time taken to cross the river is (Width of river)/(Velocity of boat w.r.t Earth) `rArr t = (800)/(2 sqrt(3)) = (400 sqrt(3))/(3) s`. 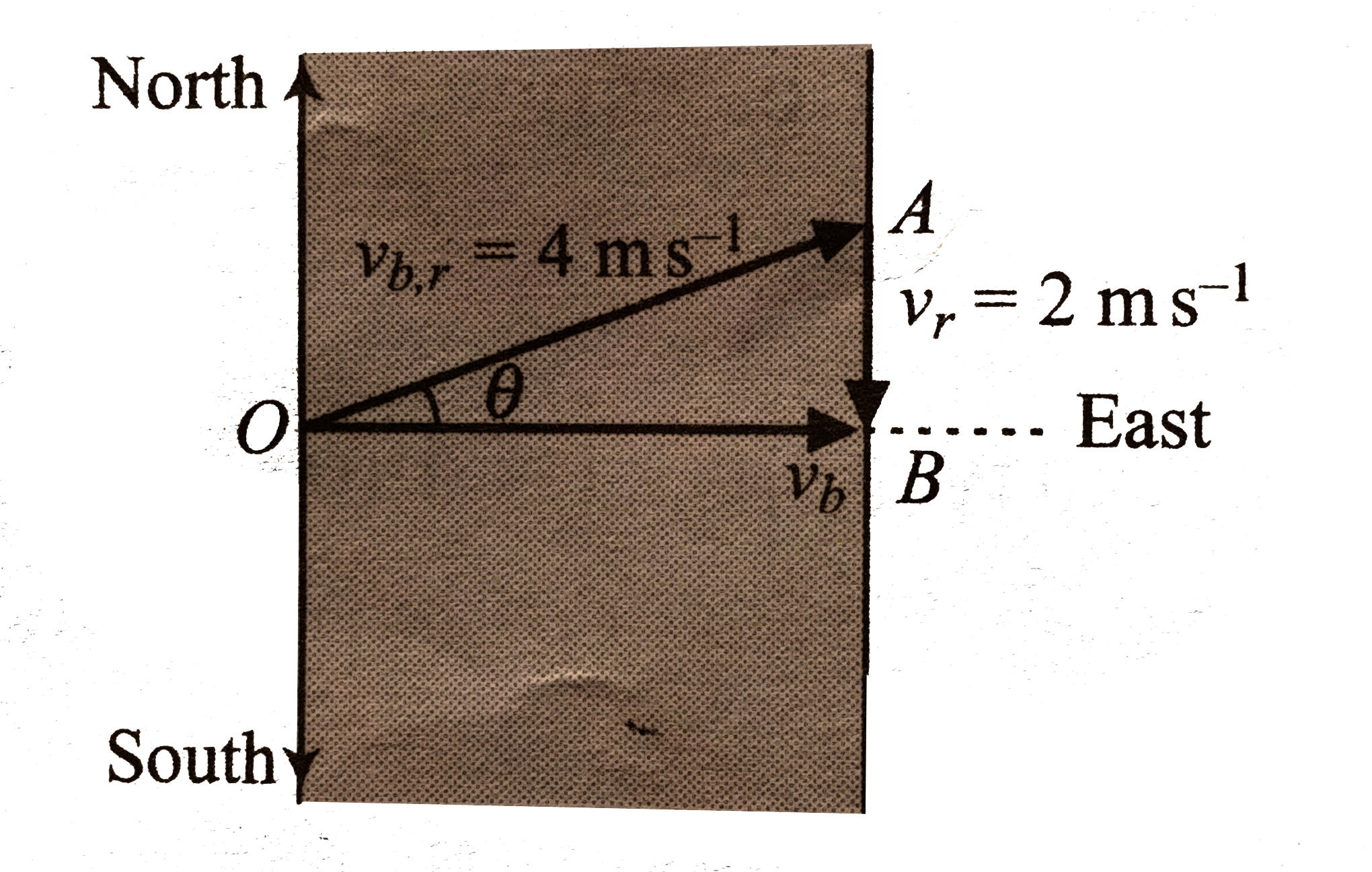 . .
|
|
Discussion
No Comment Found
Related InterviewSolutions
- What is uniform velocity
- Derive the speed time equation by calculas method
- 9×2y - 24x^2 +16y^3.factorise?
- Give me tips for preparation of physics??
- Advantage of friction
- Derivation of equation of Newton\'s Second Law of Motion that is F=ma
- Equation of projectile?
- Unit of Permeability
- Difference between vectr and scalar
- what is centripetal force ?