A log of wood of length l and mass M is floating on the surface of a river perpendicular to the banks. One end of the log touches the banks. A man of mass m standing at the other end walks towards the bank. Calculate the displacement of the log when he reaches nearer end of the log

A log of wood of length l and mass M is floating on the surface of a r

1.	A log of wood of length l and mass M is floating on the surface of a river perpendicular to the banks. One end of the log touches the banks. A man of mass m standing at the other end walks towards the bank. Calculate the displacement of the log when he reaches nearer end of the log
Answer» Solution :Let `PQ` be the log of wood. As there is no external FORCE, the CENTRE of MASS of man and the log system remains at rest. Let the bank of the river be the origin `A`. Initially, the man is at point `Q`. 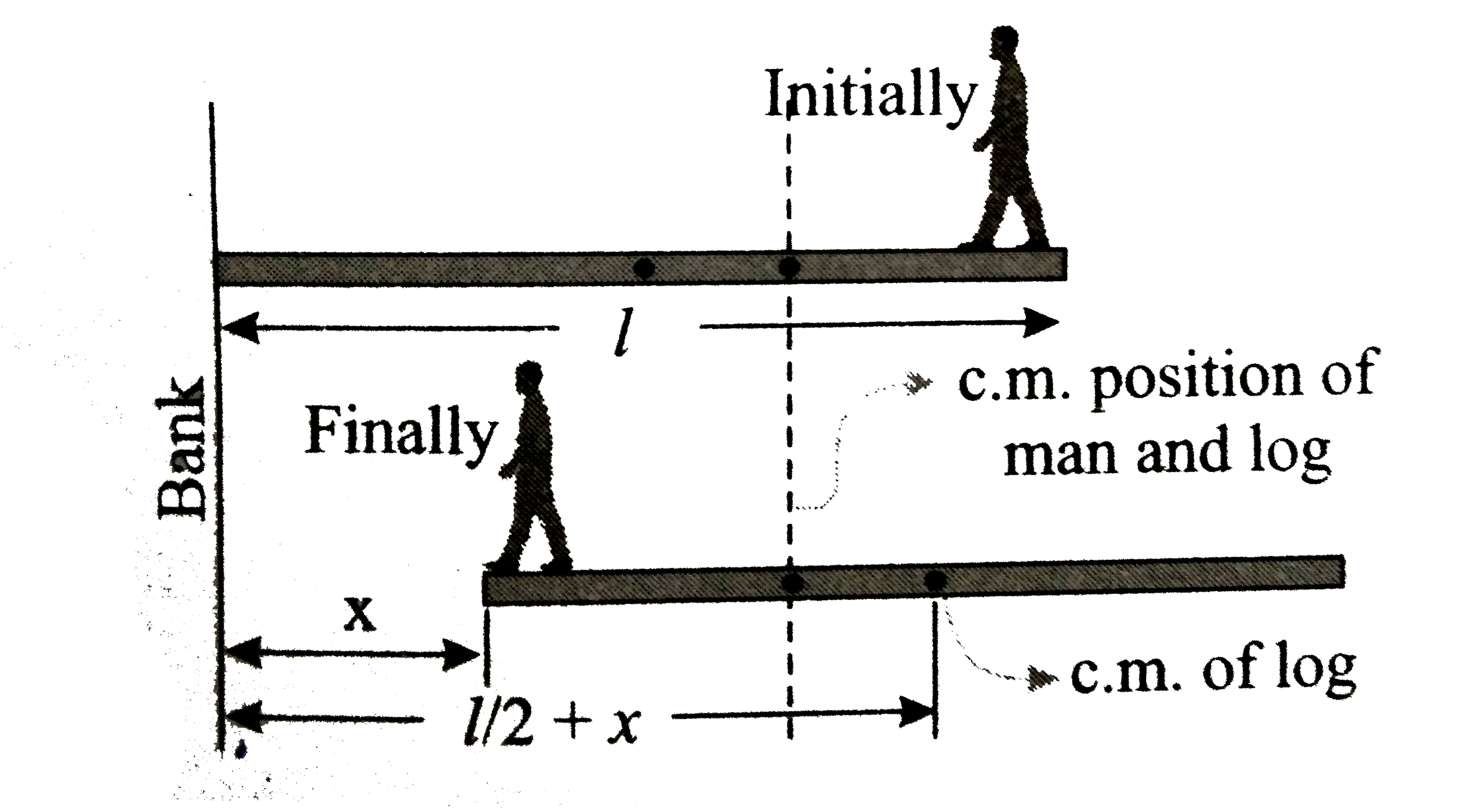Let `m=`mass of man `M=`mass of log `x=`displacement of log w.r.t GROUND (here water) `X_(CM)` (initial) `=(m(L)+m(l/2))/(m+M)` `X_(CM)`(final)`=(m(x)+M(l//2+x))/(m+M)` Now `X_(CM)`(initial) `=X_(CM)` (final) `implies ml+(Ml)/2=mx+(Ml)/2+Mx` `impliesx=(ml)/(m+M)` Hence the log moves away from the bank through a distance of `(ml)/((m+M))` Alternative method: Displacement of the log `=/_\x_(1)=x` Displacement of the man `=/_\x_(2)=l-x` Apply `m_(1)x_(1)=m_(2)x_(2)implies`(if the centre of mass remains at the same place) `impliesMx=m(l-x)impliesx(ml)/((m+M))`