1.

A massless rod S having length 2l has point masses attached to its two each as shown in Fig. The rod is rotating about an axis passing through its centre and making angle alpha with the axis. The magnitude of rate of change of momentum of rod i.e. |(dL)/(dt)| equals

Answer» <html><body><p>`<a href="https://interviewquestions.tuteehub.com/tag/2-283658" style="font-weight:bold;" target="_blank" title="Click to know more about 2">2</a> <a href="https://interviewquestions.tuteehub.com/tag/ml-548251" style="font-weight:bold;" target="_blank" title="Click to know more about ML">ML</a>^(3) omega^(2) sin <a href="https://interviewquestions.tuteehub.com/tag/alpha-858274" style="font-weight:bold;" target="_blank" title="Click to know more about ALPHA">ALPHA</a>. <a href="https://interviewquestions.tuteehub.com/tag/cos-935872" style="font-weight:bold;" target="_blank" title="Click to know more about COS">COS</a> alpha`<br/>`ml^(2)omega^(2) sin 2 alpha`<br/>`ml^(2) sin 2 alpha`<br/>`m^(1//2)l^(1//2) omega sin alpha. cos alpha`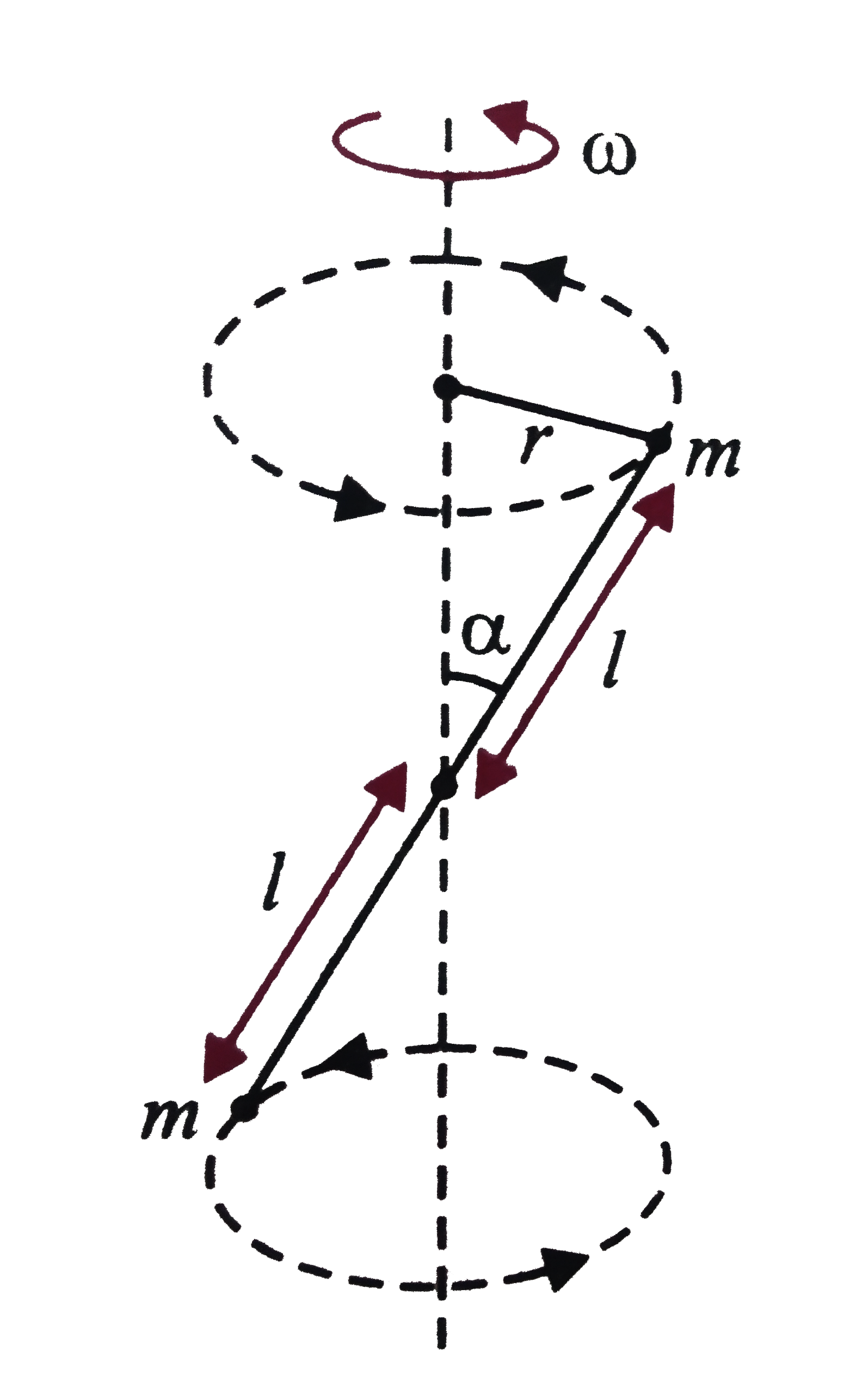</p>Solution :Refer to Fig. <br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XI_V01_C05_E01_173_S01.png" width="80%"/> <br/> The radius `r` of the circle traced by the masses is `r = l sin alpha` <br/> Angular momentum `overset rarr(L) = overset rarr(r ) xx m overset rarr(v)` <br/> `|overset rarr(L)| = r xx m omega r = m omega r^(2)` <br/> `= momega (l sin alpha)^(2) = m omegal^(2) sin^(2)alpha` <br/> `(dL)/(dt) = m omegal^(2) sin alpha cos alpha(d alpha)/(dt)` <br/> `= m omegal^(2) (sin 2 alpha) omega = m omega^(2)l^(2) sin 2 alpha`</body></html>


Discussion

No Comment Found

Related InterviewSolutions