A non-homogeneous sphere of radius R has the following density variation : rho{{:(rho_(0),rleR//3),(rho_(0)//2,(R//3) lt r le (3R//4)),(rho_(0)//8,(3R//4) lt r le R):} The gravitational field at a distance 2R fromthe centre of the sphere is

A non-homogeneous sphere of radius R has the following density variati

1.	A non-homogeneous sphere of radius R has the following density variation : rho{{:(rho_(0),rleR//3),(rho_(0)//2,(R//3) lt r le (3R//4)),(rho_(0)//8,(3R//4) lt r le R):} The gravitational field at a distance 2R fromthe centre of the sphere is
Answer» `0.1piGRrho_(0)` `0.2piGRrho_(0)` `0.3piGRrho_(0)` `0.4piGRrho_(0)` Solution :(a) The gravitational field at a distance 2R from the CENTRE of the sphere is `E=(GM)/((2R)^(2))` where M is the mass of the WHOLE sphere. 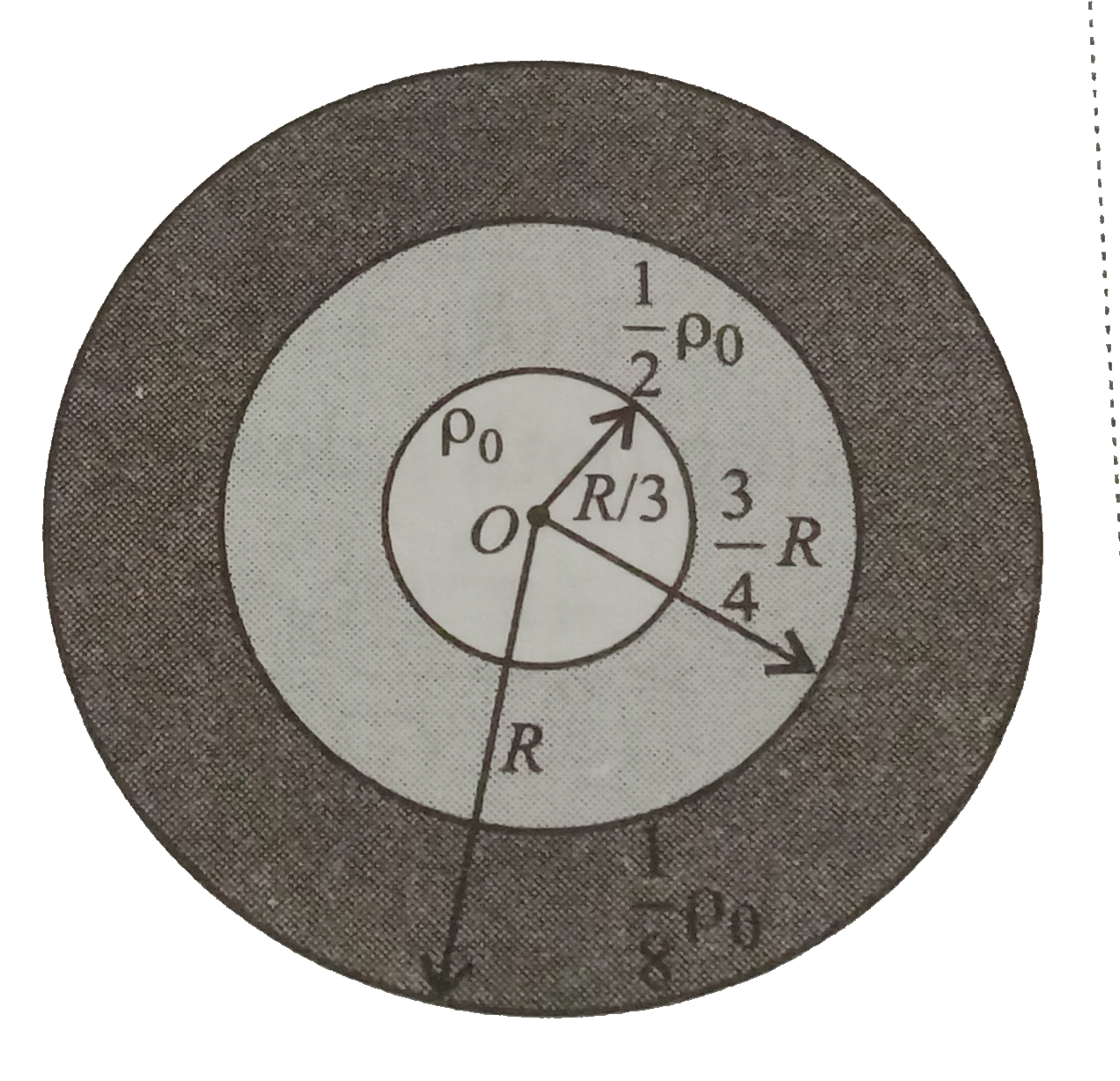Here, `M=(4)/(3)pi((R)/(3))^(3) rho_(0)+{(4)/(3)pi((3)/(4)R)^(3)-(4)/(3)pi((R)/(3))^(3)}(rho_(0))/(2)+{(4)/(3)PIR^(3)-(4)/(3)pi((3)/(4)R)^(3)}(rho_(0))/(8)` `=(4)/(3)piR^(3)rho_(0){(1)/(27)+(27)/(128)-(1)/(54)+(1)/(8)-(27)/(512)}` `=(4)/(3)piR^(3)rho_(0){(512+2916+256+1728-729)/(13824)}` `=(4)/(3)piR^(3)rho_(0){(5156-985)/(13824)}=(4)/(3)piR^(3)rho_(0){(4171)/(13824)}` `=0.402piR^(3)rho_(0)` `:. E=(G(0.402piR^(3)rho_(0)))/((2R)^(2))=0.1piGRrho_(0)`