InterviewSolution
Saved Bookmarks
| 1. |
A particle of mass m is attached to one end of missless rigid non-conducting rod of length l. Another particle of the same mass is attached to the other end of the rod. Two particles carry charges +q and -q . Thisarrangement is held in the region of uniform electric field E such that the rod makes and angle theta (lt 5^(@)) withthe fielddirection. Find an expression for the minimum time that is needed for the rod to become parallel to the field after it is set free. |
|
Answer» Solution :As the rod has twocharges of EQUAL MAGNITUDE(be opposite in nature), the torqueacting on the rod, `tau=qE xx l sin theta` or, `tau =qE l theta""[ becausetheta LT 5^(@)]` We know, `tau=I alpha` [where I = moment ofinertia and `alpha` = angular acceleration] 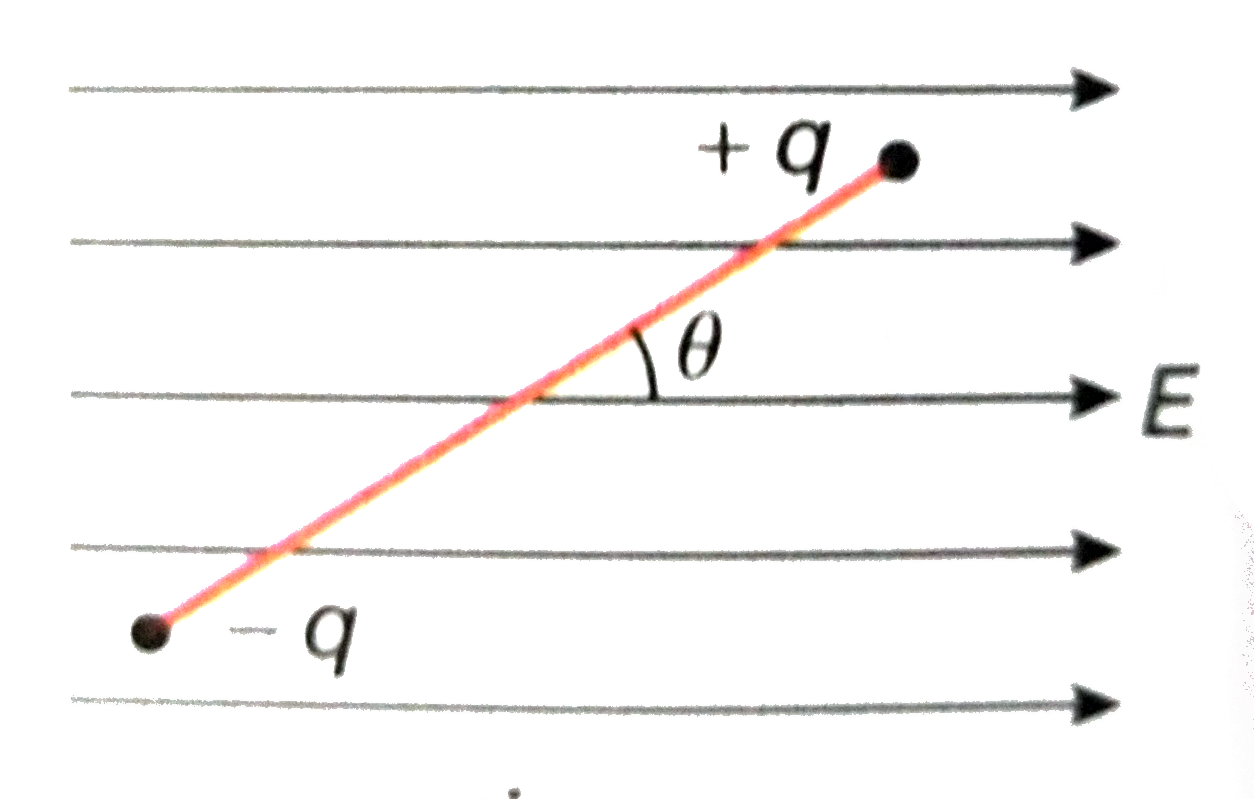 Hence, `I alpha=q E l theta or, alpha=(q E l theta)/(I)` `therefore` TIME period, `T=2pi sqrt(("angular displacement")/("angular acceleration"))=2pi sqrt((I)/(qE l))` Now, moment ofinertiaof the DIPOLE, `I=[((l)/(2))^(2)+((l)/(2))^(2)]m=(1)/(2) ml^(2)` `therefore T=2pisqrt((ml^(2))/(2qEl))=2pi sqrt((ml)/(2qE))` `therefore ` Required time, `t=(1)/(4)xx "time period"=(T)/(4)=(pi)/(2) sqrt((ml)/(2qE))` |
|