Saved Bookmarks
| 1. |
A rope thrown over a pulley has a on one of its ends and a counterbalancingmass M on its other end. The man whose mass is m, climbs upwards by vec/_\r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system. |
|
Answer» Solution :Let displacement of counterweight be `/_\y` therefore the dispacement of ladder will be `(-/_\y)`. Displacement of man `/_\_(y_m)=/_\_(y_(m,l))+/_\_(y_l)` `Y_(mj)=` displancement of man w.r.t of ladder `=/_\vecr` `y_m=(/_\r-/_\y)` HENCE displacement of centre of mass of the system `/_\vecr_c=(M_("mass")/_\vecr_("mass")M_("ladder")+/_\vecr_("ladder")+M_("mean")/_\vecr_("man"))/(M_("mass")+M_("ladder")+M_("man"))` `/_\r_(c)=(M/_\y+(M-m)-(/_\y)+m(/_\r-/_\y))/(M+(M-m)+m)` `implies /_\r_(c)=(m/_\r)/(2m)("upward")` Method 2: All the bodies of the system are initially at rest. The rope tension is the same both as on the left and the right hand side, at every INSTANT and consequently the momenta of the counterbalancing mass `(vecp_(1))` and the ladder with the Man `(vecp_(2))` are equal at any moment of time. i.e., 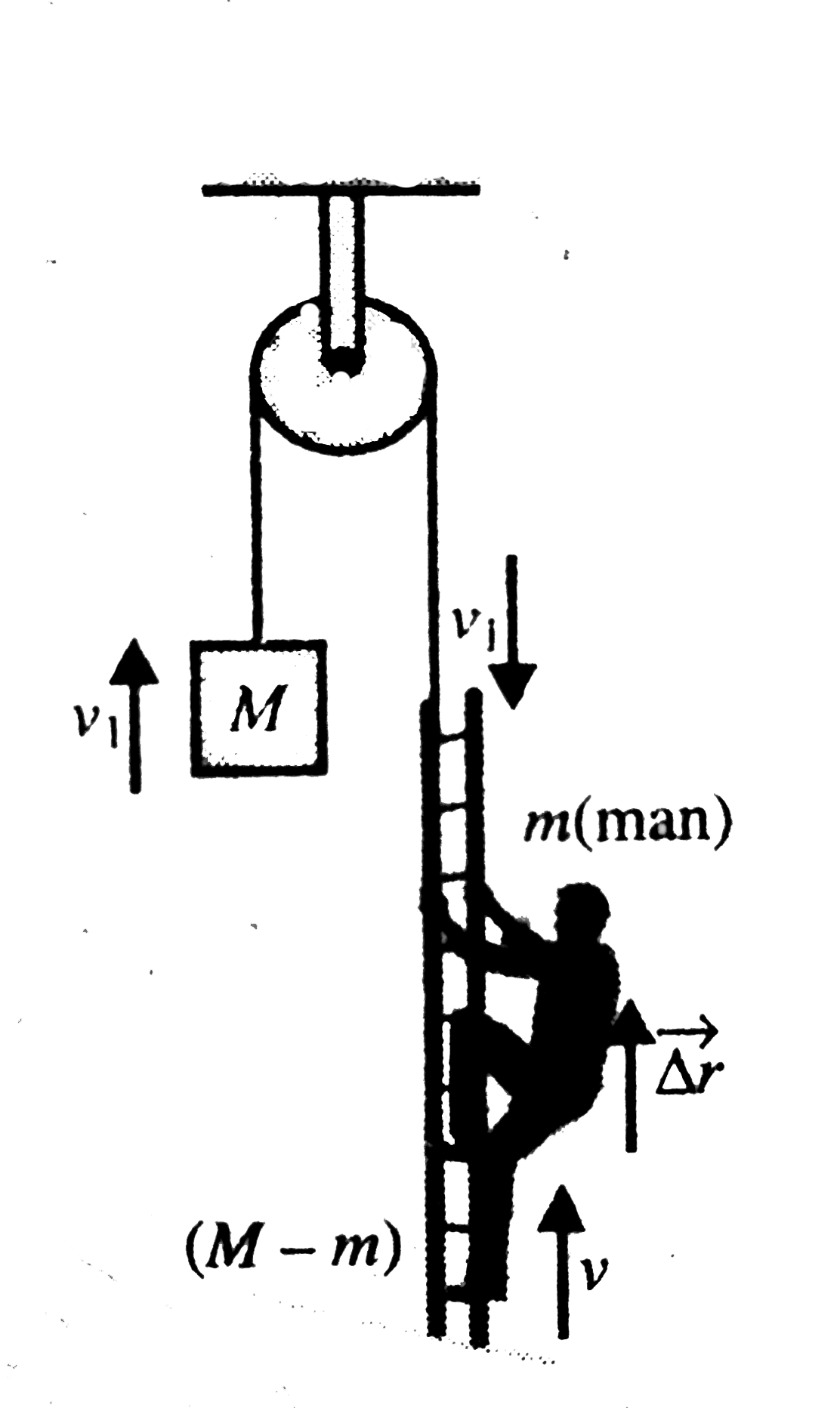 `vecp_(1)=vecp_(2)` or `Mvecv_(1)=mvecv+(M-M)vecv_(1)`............i Here `vecv_(1)` and `vecv` are the velocities of the mass and the man respectively. Velocity of man`vecv_("man") vecv_("man, ladder")+vecv_("ladder")=v'-v_(1)`...........ii Where `vecv'` is the man's velocity relative of the ladder. From eqn i and ii we OBTAIN `vecv_(1)=(m/(2M))vecv'` on the other hand the momentum of the centre of mass is `vecp=vecp_(1)+vecp_(2)=2vecp_(1)` or `2Mvecv_(C)=2M.vecv_(1)` or `vecv_(C)=vecv_(1)=(m/(2m))vecv'` are finally the desired displacement is `/_\vecr_(C)=intvecv_(C).dt=m/(2m)intvecv'dt=m/(2M)/_\vecr` or displacement of centre of mass of system is `/_\vecr_(C)=m/(2M)/_\vecr` As system I and system II both are having same mass and experiene equal force. Both starts from rest. hence displacement of centre of masses FO systems should be equal. As the system I has only one object, the diaplacement of the object will be same as the displascement of its centre of mass which is `/_\y` upward. hence the displacement of centre of mass of system II will so be `/_\y` upward `(/_\vecy_(cm))_("systemI")=(/_\vecy_(cm))_("systemII")=/_\y("upward") ` `implies /_\y=(m(/_\r-/_\y)+(M-m)(-/_\y))/(m(M-m))` `implies /_\y=(m/_\r)/(2M)("upward")` 
|
|