A uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a//4 above the base. a. What is the minimum value of F for which the cube begins to tip about an edge? b. What is the minimum value of its so that toppling occurs? c. If mu=mu_("min") find minimum force for topping. d. Find minimum mu_(s) so that F_("min") can cause toppling.

A uniform cube of side 'a' and mass m rests on a rough horizontal tabl

1.	A uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a//4 above the base. a. What is the minimum value of F for which the cube begins to tip about an edge? b. What is the minimum value of its so that toppling occurs? c. If mu=mu_("min") find minimum force for topping. d. Find minimum mu_(s) so that F_("min") can cause toppling.
Answer» Solution :a. In the limiting case normal reaction will PASS through `O`. The cube will tip about `O` if torque of `F` about `O` exceeds the torque of `mg` HENCE `F(a/4)gtmg(a/2)` 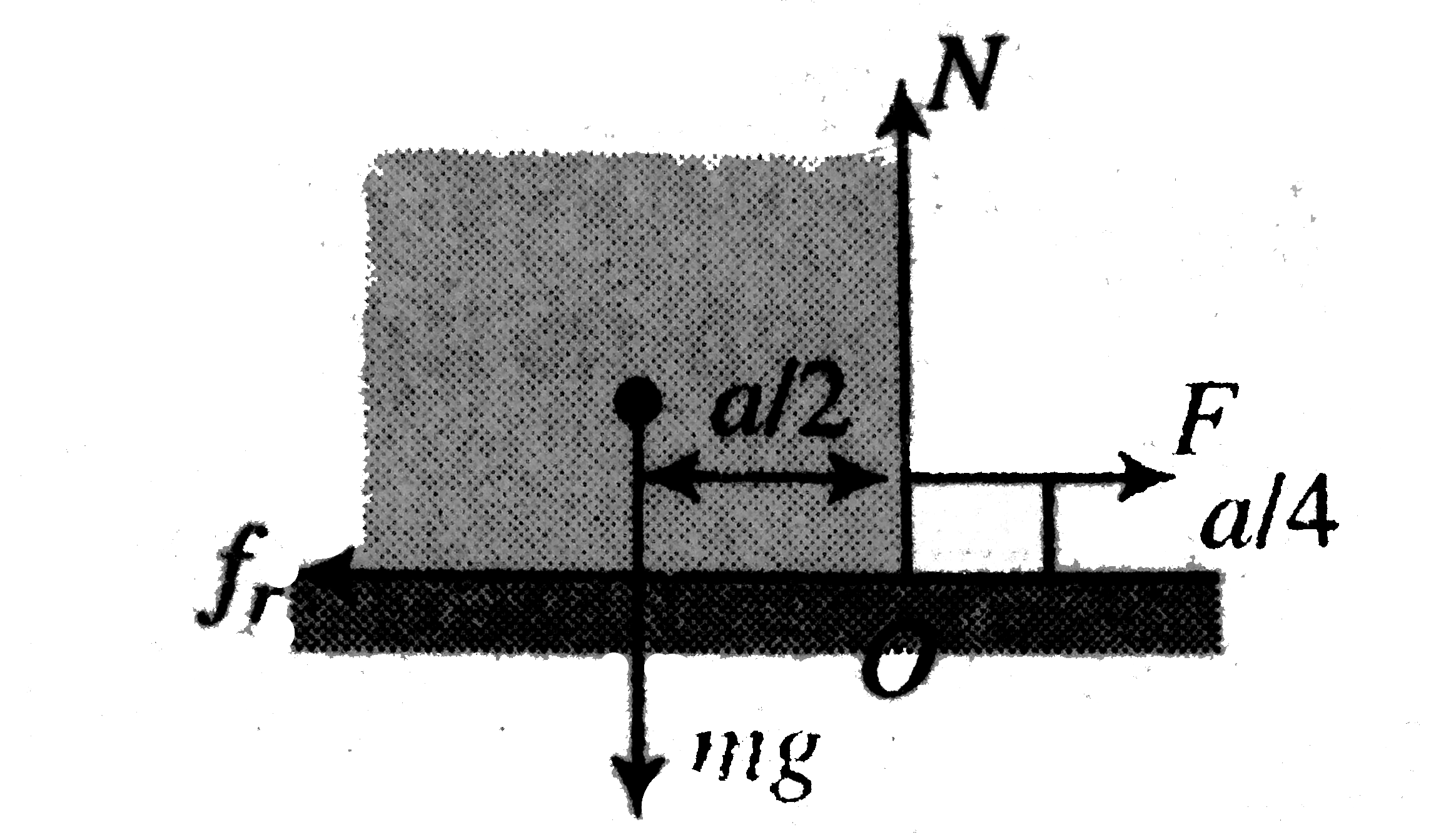or `Fgtmg` Therefore minimum value of `F` is `2mg` b. In thiscase SINCE it is not acting at `COM`, toppling can occur even after body started sliding because increasing the torque of `F` about `COM`. Hence `mu_(min)=0`, c. Now body is sliding before toplling `O` is not `IAR`, torque equation can not be APPLIED across it. It can now be applied about `COM`. `Fxxa/4=Nxxa/2` ......i `N=mg` ...........ii From i and ii `F=2mg` d. `Fgt2 mg` ............iii from sol a `N=mg` `Fmu_(s)N=mu_(s)mg`.........iv from i and ii `mu_(s)=2`.......v