Saved Bookmarks
| 1. |
A uniform plate of mass m is suspended in each of the ways shown. For each case determine immediately after the connection at Bhas been released , (a) the angular acceleration of the plate. (b) the acceleration of its mass center. |
|
Answer» `I_(Z Z') = I_(XX') + I_(YY')` `I_(Z Z') = (m(c//2)^(2))/(12) +(mc^(2))/(12) rArr I_(Z Z') = (5mc^(2))/(48)` from parallel axis theorem `I_(A) = I_(Z Z') + mr^(2)` `I_(A) = (5 mc^(2))/(48) + m(( c)/(4) SQRT(5))^(2)` `I_(A) = (5mc^(2))/(48) + (m xx 5c^(2))/(16)` `I_(A) = (5mc^(2))/(12)` (i) As 'B' is RELEASED (a) `tau = I ALPHA` `mg xx (c)/(2) = ((5mc^(2))/(12)) alphaalpha = (1.2 g)/(c)` (b) `a_(CM) =a_(t) cos theta (- hati) + a_(t) sin theta (-hat j) and a_(t) = r alpha` `a_(CM) = alpha (r costheta) (-hat i) + alpha r sin theta (-hat j)` `a_(CM) = alpha(c)/(4) (-hat i) + prop (c)/(2) (-hatj) rArr a_(CM) = -(alphac)/(4) [hat i + 2 hatj]` `a_(CM) = -0.3[hat i + 2 hat j] g` (b) `2 F = mg F = (mg)/(2)` (spring force) As the spring at `B` is cut for transverse motion `mg - F = ma` `(mg)/(2) = ma a = (g)/(2) darr` for rotational motion with resect to `A` `(mg -ma) ( c)/(2) = I alpha` (`ma` in pssudo force) `(mg)/(2) xx ( c)/(2) = ((5 mc^(2))/(12) alpha` `alpha = (2.4 g)/( c) (c.w.)`. 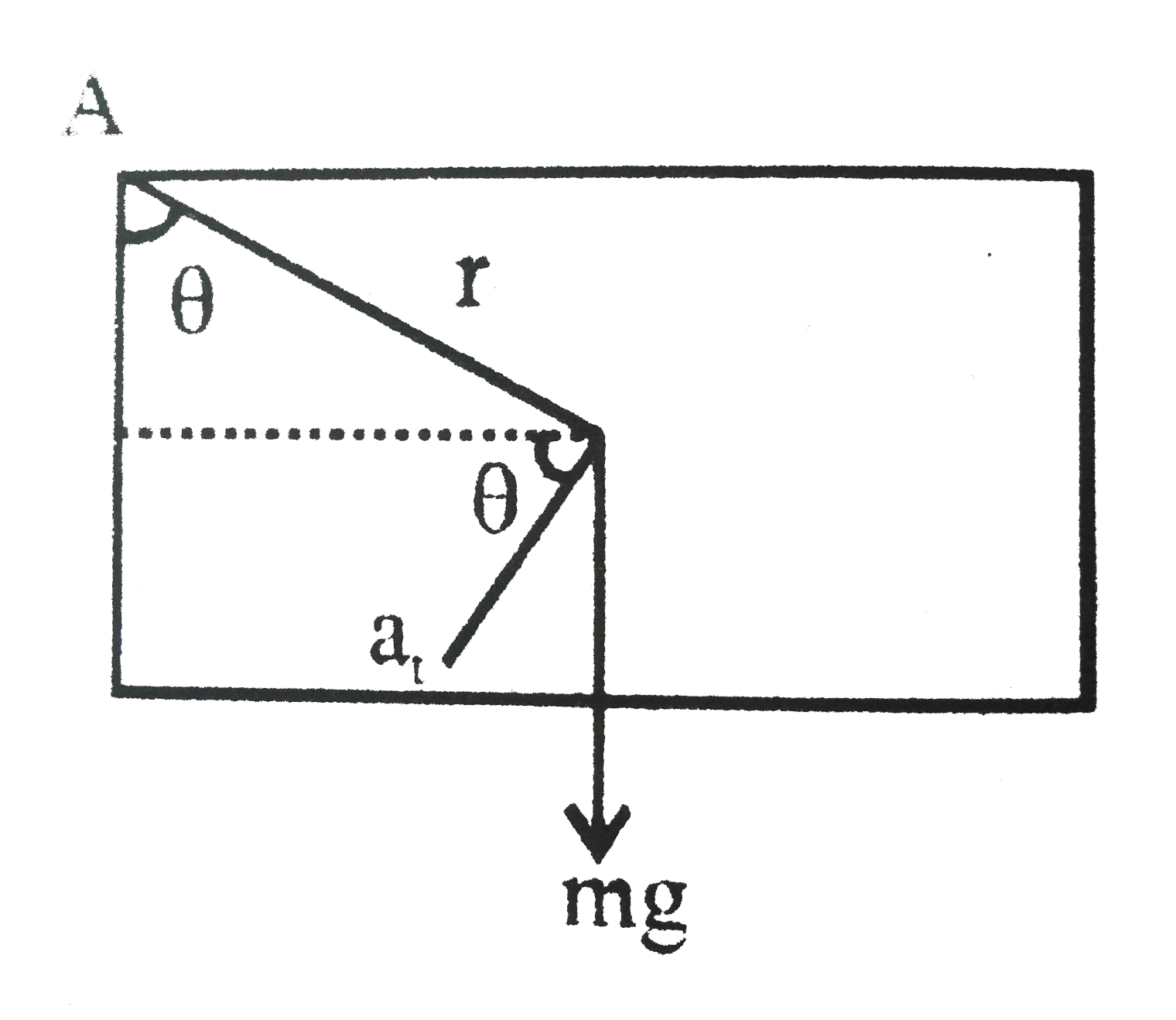 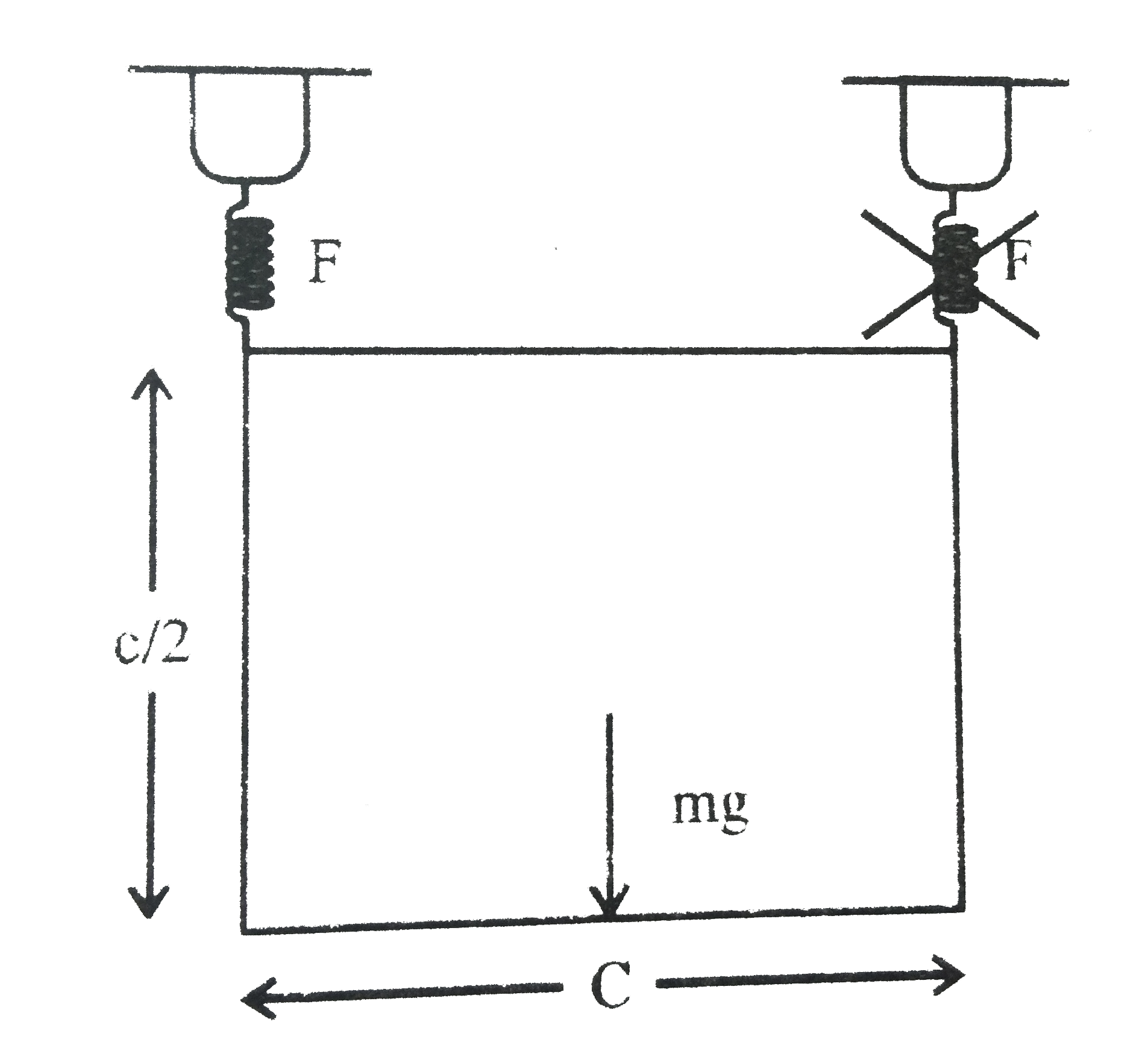 . .
|
|
Discussion
No Comment Found
Related InterviewSolutions
- What is uniform velocity
- Derive the speed time equation by calculas method
- 9×2y - 24x^2 +16y^3.factorise?
- Give me tips for preparation of physics??
- Advantage of friction
- Derivation of equation of Newton\'s Second Law of Motion that is F=ma
- Equation of projectile?
- Unit of Permeability
- Difference between vectr and scalar
- what is centripetal force ?