Saved Bookmarks
| 1. |
An equilateral triangle ABC is formed by two copper rods AB and BC and one is aluminium rod which heated in such a way that temperature of each rod increases by DeltaT. Find change in the angle angleABC. (Coefficient of linear expansion for copper is alpha _(1). and for aluminium is alpha2.). |
|
Answer» Solution :Suppose,`AB = l _(1), AC =_(2) and BC = l _(3)` `therefore COS theta = ( l _(3) ^(2) + l _(1) ^(2) - l _(2) ^(2))/( 2 l _(3) l _(1))`where ` angleABC = theta ` `therefore 2l _(3) l _(1) cos theta = l _(3) ^(2) + l_(1) ^(2) - l _(2) ^(2)` 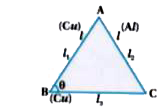 Integrating on both side, `2 ( l _(3) dl _(1) + l _(1) dl _(3)) cos theta- 2 l3l _(1) sin theta d theta =2l _(3) dl _(3) +2l _(1) dl _(1) -2l _(2) dl _(2)` Dividing by 2, `(l_(3) dl _(1) + l _(1) xx dl _(3)) cos theta -l _(3) l _(1) sin theta d theta =l_(3) dl _(3) + l _(1) dl _(1) - l _(2) dl _(2)` Now `dl _(1) = l _(1) alpha _(1) Delta T, dl _(2) = l _(1) alpha _(2) Delta T, dl _(3) = l _(3) alpha _(3) Delta T ` then, `(l _(3) xx l _(1) alpha _(1) Delta T + l _(1) xx l _(3) alpha _(3) Delta T) cos theta - l _(3) l _(1) sin theta d theta =` `l _(3) xx l _(3) alpha _(3) Delta T + l_(1) xx l _(1) alpha _(1) Delta T - l _(2) xx l _(2) alpha _(2) Delta T` Now let `l _(1) =l _(2) = l _(3) = l and alpha _(3) = alpha _(1)` `therefore (l ^(2) alpha _(1) Delta T + l ^(2) alpha _(1) Delta T) cos theta - l ^(2) sin theta d theta = l ^(2) alpha _(1) Delta T +^(2) alpha _(1) Delta T - l ^(2) alpha _(2) Delta T` `cos theta = cos 60^(@) = 1/2 ` (Equilateral triangle) `therefore 2l ^(2) alpha _(1) Delta T xx 1/2 - l ^(2) sin theta d theta = 2l alpha _(1) Delta T - l ^(2) alpha _(2) Delta T` `therefore l alpha _(1) Delta T - l ^(2) sin theta d theta = 2l ^(2) alpha _(1) Delta T - l ^(2) alpha _(2) Delta T ` Dividing by `l ^(2),` `alpha _(1) Delta T - sin thetad theta = 2 alpha _(1) Delta T - alpha _(2) Delta T` `- alpha _(1) Delta T + alpha _(2) Delta T = sin theta d theta ` `therefore d theta = ((alpha _(2) - alpha _(1))Delta T )/( sin theta )` `therefore d theta =(2 (alpha _(2) - alpha _(1)) Delta T)/( SQRT3) [ because sin theta = sin 60^(@) = (sqrt3)/(2) ]` |
|