Saved Bookmarks
| 1. |
Calculate coefficient of correlation by means of ranking method from the following data : |
Answer» Solution :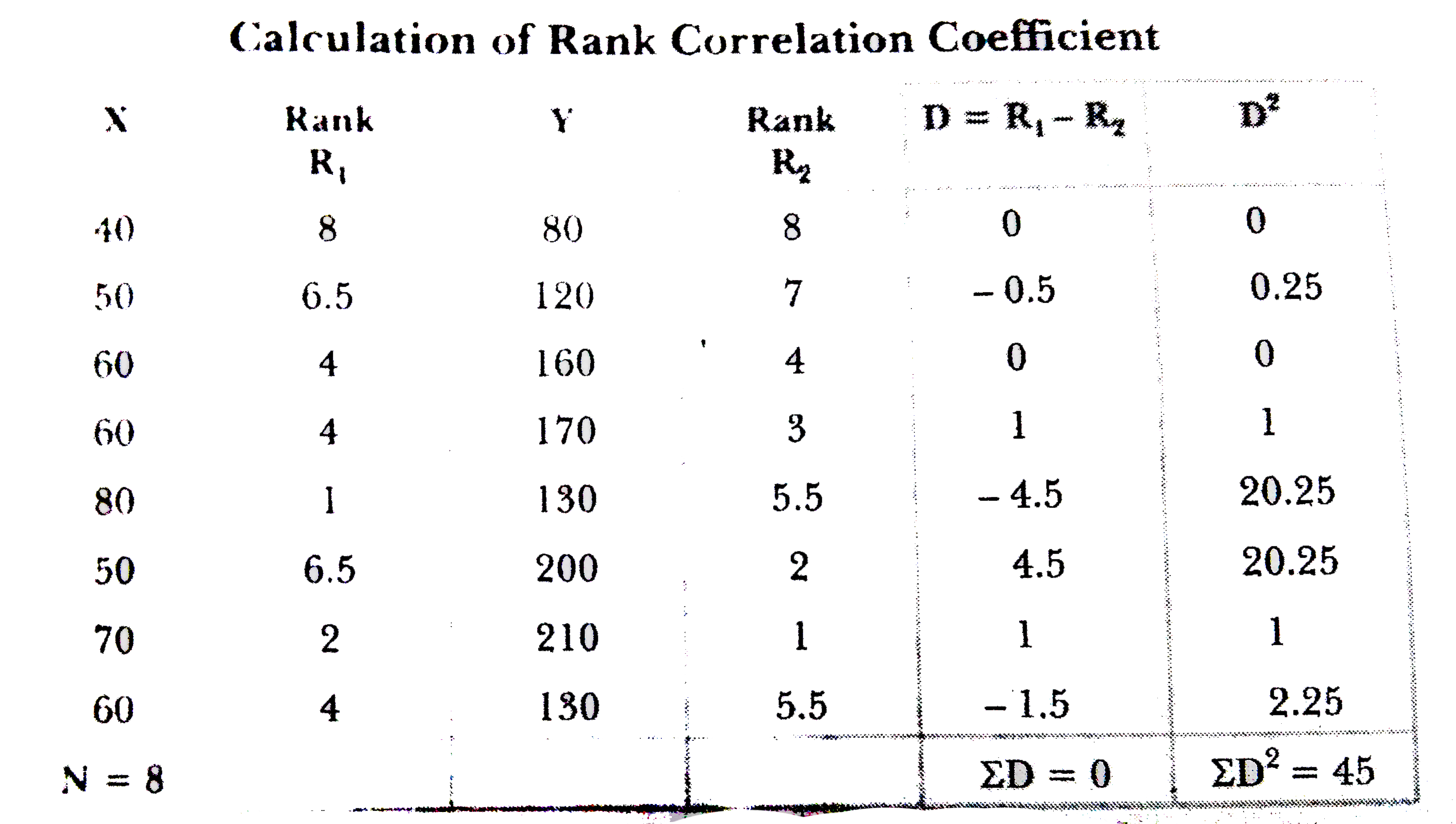 In this question in X series, the values 60 and 50 are repeated thrice and TWICE. The averages rank for the VALUE 60 is `4(3+4+5 div 3)` while for the value 50 it is 6.5 `(6+7 div 2)`. In both the cases, the correlation factor will be `(1)/(12)(3^(3)-3) " and " (1)/(12)(2^(3)-2)` respectively . In series Y, the 130 is repeated twice. The average rank for the value 130 is 5.5 `(5+6 div 2)`. In this case, correlation factor will be `(1)/(12)(2^(3)-2)`. `r_(k)=1-(6[SUMD^(2)+(1)/(12)(m_(1)^(3)-m_(1))+(1)/(12)(m_(2)^(3)-m_(2))+(1)/(12)(m_(3)^(3)-m_(3))])/(N^(3)-N)` Here, `sumD^(2)=45,m_(1)=3,m_(2)=2,m_(3)=2N=8` By substituting values in the above formula, we get `r_(k)=1-(6[45+(1)/(12)(3^(3)-3)+(1)/(12)(2^(3)-2)+(1)/(12)(2^(3)-2)])/((8)^(3)-8)` `=1-(6[45+(1)/(12)(24)+(1)/(12)(6)+(1)/(12)(6)])/(512-8)` `=1-(6(45+2+(1)/(2)+(1)/(2)))/(504)=1-(6(48))/(504)=1-(288)/(504)=1-0.571=0.429` Coefficient of Rank Correlation `(r_(k))=0.429` |
|
Discussion
No Comment Found
Related InterviewSolutions
- Assumption of ordinal apporch
- Critical appraisal of methods of collection of data
- Different between microeconomics and macroeconomics
- What happense when ic slops downwards
- Implications of perfect competition in forms of market
- If price of mango rises demand will ?
- What is statistical table? Explain briefly tha main characteristics of a good statistical table.
- What is production possibility curve
- Explain any three factor which affect the supply of a commodity
- What do you understand by the increasing returns to scale