Saved Bookmarks
| 1. |
Define orbital velocity and establish an expression for it. |
|
Answer» Solution :(i) ORBITAL velocity is the velocity given to artificial satellite so that it may startrevolingaround the earth. Expression for orbital velocity Consider a satellite of mass .m. is revolving around the earth in a circularorbit of radius .r. at aheight .h. from the SURFACE of the earth. Let .M. be the mass of the earth and .R. be the radius of the earth Therefore , r = R + h The centripetal force that is required to revolve the satellite ` = (mv_0^2)/(r )` where `V_0` is orbital velocity Orbital velocity is produced by the gravitational force b/w the earth and the satellite ` = (GMm)/(r^2)` 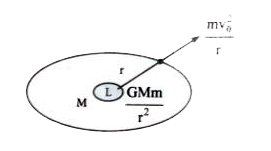 ` therefore (mv_2^2)/(r ) = (GMm)/(r^2)` ` v_0^2 = (GM)/( r) = (GM)/( R + h)` ` v_0 = sqrt((GM)/(r )) = sqrt((GM)/(R +h))` This is the expression for the orbital velocity. (ii)Mass of the earth `M = 6 xx10^24 kg ` Radius of the earth R = 64000 km The height of the artificial satellite from the earth (h) = 1000 km Gravitational constant ` (G) = 6.67 xx 10^(-11) Nm^(-2) kg^(-2)` Orbitalvelocity ` V_0 = sqrt((GM)/(R+h))` ` = sqrt( (6.7 xx 10^(-11) xx 6 xx 10^24)/(64000+1000)) = sqrt( (40.02 xx 10^13)/(65 xx 10^3)) = sqrt( (400.2)/(65)) = sqrt(6.1569)` ` V_0 = 2.48 ms^(-1)` |
|