1.

Derive an expression for the acceleartion of the bodysliding down a frictionless surface

Answer» <html><body><p></p>Solution :Whenan objectof massmslideson africtionalsurfaceinclinedat anangle `theta` as shownin the figurethe forcesactingonitdecides theaccelerationof <a href="https://interviewquestions.tuteehub.com/tag/theobject-1409990" style="font-weight:bold;" target="_blank" title="Click to know more about THEOBJECT">THEOBJECT</a>(b)speedof theobject when it reachesthe bottom .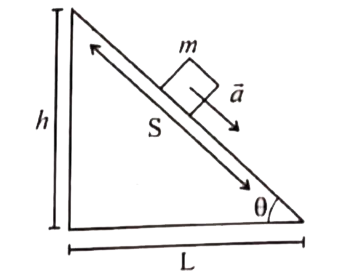<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PRE_GRG_PHY_XI_V02_C03_E02_147_S01.png" width="80%"/> <br/>The forceactingon theobject is<br/> (i)Downwardgravitational force (mg) <br/> (<a href="https://interviewquestions.tuteehub.com/tag/ii-1036832" style="font-weight:bold;" target="_blank" title="Click to know more about II">II</a>) Normalforceperpendicularto inclinedsurface (N)<br/> theblockis assumedto be apointmass[Inorder to drawthe freebodydiagram in figure(a)].Sincethe motionis on theinclinedsurfacethecoordinatesystemparallelto tehinclinedsurfaceis chosenas shown in thefigure (b)It isnotedthat theanglemadebythe gravitationalforcewith theperpendicularto the surfacesi <a href="https://interviewquestions.tuteehub.com/tag/equalto-974074" style="font-weight:bold;" target="_blank" title="Click to know more about EQUALTO">EQUALTO</a> theangleof inclination `theta` as shown inin figure<br/> `-mg cos theta hat(j)+ N hat(j) = 0`(No acceleration ) <br/> Bycomparingthecomponentson bothsidesN- mg cos `theta = 0` <br/> `N= mg cos theta`<br/> Themagnitude of normalforce(N)exertedby tghesurfaceis <a href="https://interviewquestions.tuteehub.com/tag/equivalentto-974754" style="font-weight:bold;" target="_blank" title="Click to know more about EQUIVALENTTO">EQUIVALENTTO</a> mgcos `theta` . Theobjectslidesalongthe x direction . <br/> Bycomparingthe componentson bothsideswe canequate <br/> `mg sin theta= ma ` <br/> Theaccelerationof theslindingobjectis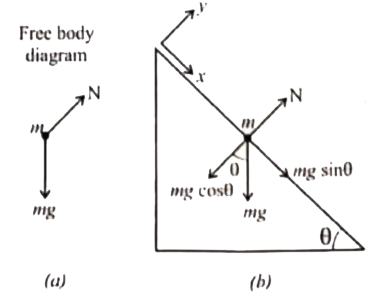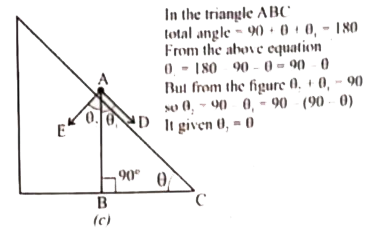<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PRE_GRG_PHY_XI_V02_C03_E02_147_S02.png" width="80%"/> <br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PRE_GRG_PHY_XI_V02_C03_E02_147_S03.png" width="80%"/> <br/> Notethat theacceleratindependson theangleinclination `theta`</body></html>


Discussion

No Comment Found

Related InterviewSolutions