Saved Bookmarks
| 1. |
Earth's orbit is an ellipse with eccentricity 0.0167. Thus, the earth's distance from the sun and speed as it moves around the sun varies from day-to-day. This means that the length of the solar day is not constant through the year. Assume that the earth's spin axis is normal to its day. A day should be taken from noon to noon. Does this explain variation of length of the during the year ? |
Answer» Solution :Consider the DIAGRAM. Let `m` be the mass of the earth, `v_(p), v(a)` be the velocity of the earth at perigee and apogee respectively. Similarly, `omega_(p)` and `omega_(a)` are corresponding angular velocities. 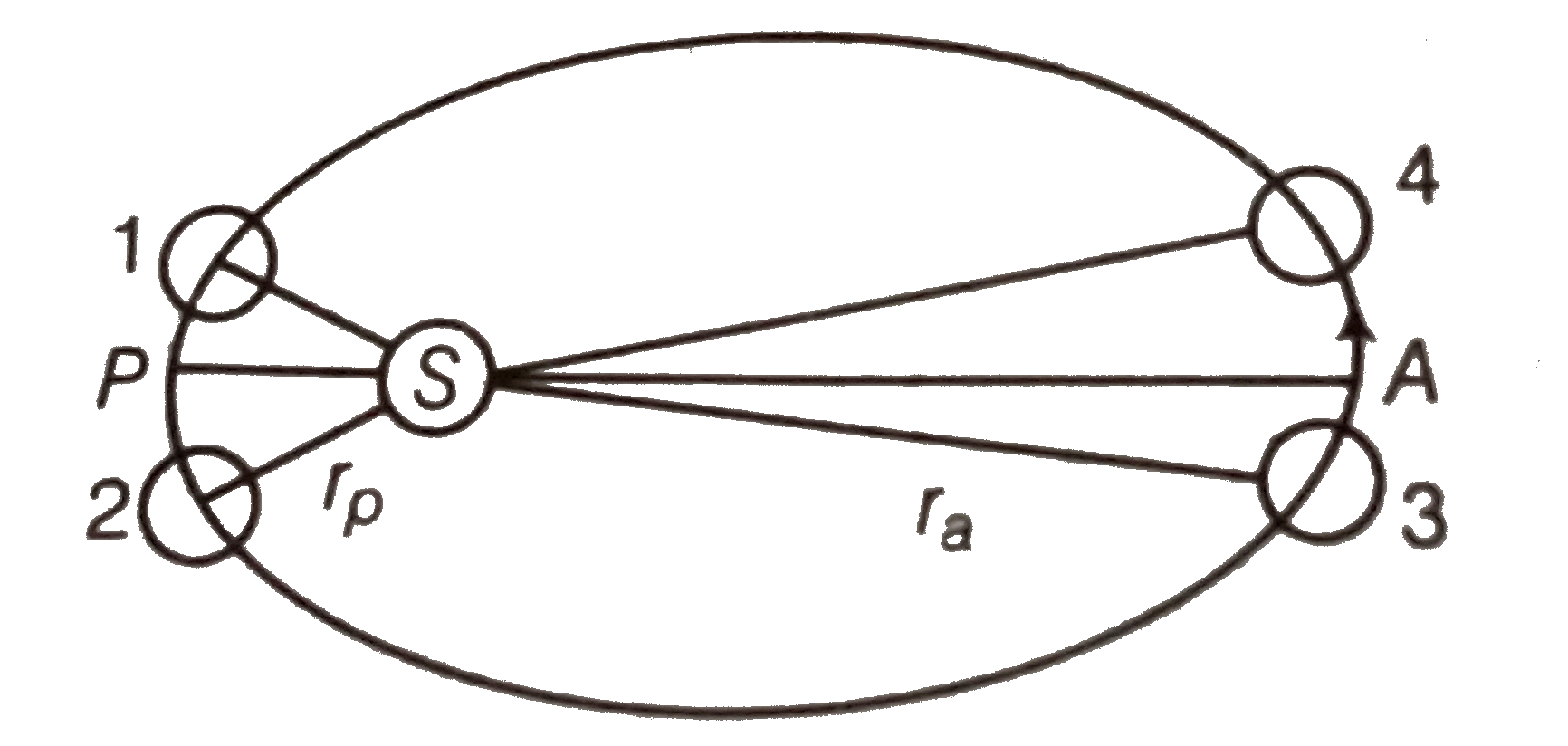 Angular momentum and areal velocity are constant as the earth orbits the sun At perigee, `r_(p)^(2) omega_(p) = r_(a)^(2) omega_(a)` at apogee ....(i) If a is the semi-major axis of the earth's orbit, then `r_(p) = a(1 - e) " and" r_(a) = a (1 + e)`....(ii) `:. (omega_(p))/(omega_(a)) = ((1 + e)/(1 - e))^(2), e = 0.0167` [from Eqs. (i) and (ii)] `:. (omega_(p))/(omega_(a)) = 1.0691` Let `omega` be angular speed which is geometric mean of `omega_(p)` and `omega_(a)` and corresponds to mean solar day, `:. ((omega_(p))/(omega)) ((omega)/(omega_(a))) = 10691` `:. (omega_(p))/(omega) = (omega)/(omega_(a)) = 1034` If `omega` corresponds to `1^(@)` per day (mean angular speed), then `omega_(p) = 1034^(@)` per day and `omega_(a) = 0.967^(@)` per day. Since, `361^(@) = 24`, mean solar day, we get 361.034 which corresponds to `24h, 8.14''` (8.1'' longer) and `360.967^(@)` corresponds to `23h 59 min 52''` (7.9'' smaller). This does not explain the actual VARIATION of the length of the day during the year. |
|