InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
Figure 22-26a shows a plastic rod with a uniform charge -Q. It is bent in a 120^(@) circulararc of radius r and symmetrically paced across an x axis with the origin at the center of curvature P of the rod. In terms of Q and r, what is the electric field vecE due to the rod at point P? |
|
Answer» Solution :KEY IDEAS Because the ROD has a continuous charge distribution, we must find an expression for the electric fields due to differential elements of the rod and then sun those fields via calculus. 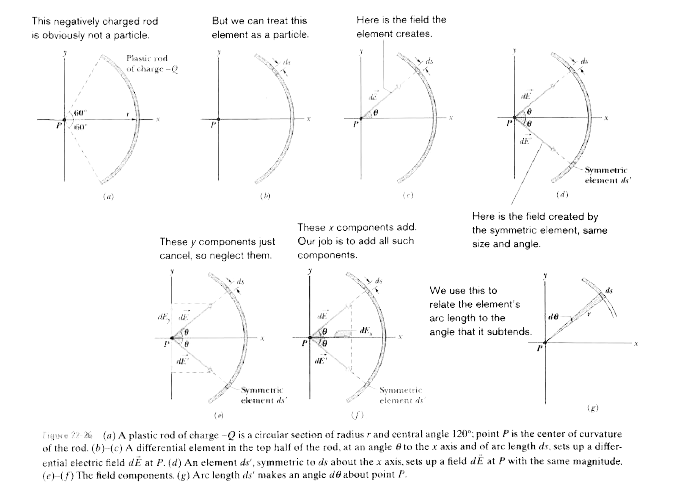 An element :Consider a differential element having arc length ds and located at an angle `theta` above the x axis (Figs. 22-26b and c). IF we let `lambda` represent the linear charge density of the rod, our element ds has a differential charge of magnitude `dq=lambda ds. "" (22-35)` The element.s field: Our element produces a differential electric field`d vecE` at point P, which is a distance r from the element. Treating the element as a point charge, we can rewrite Eq. 22-3 to express the magnitude of `d vecE` as `dE=(1)/(4pi in_(0)) (dq)/(r^(2))=(1)/(4pi in_(0)) (lambda ds)/(r^(2)). ""(22-36)` The direction of `d vecE` is toward ds because charge dq is negative. Symmetric PARTNER: Our element has a symmetrically located (mirror image) element ds. in the bottom half of the rod. The electric field `d vecE.` set up at P by ds. also has the magnitude given by Eq. 22-36, but the field vector points toward ds. as shown in Fig. 22-26d. If we resolve the electric field vectors of ds and ds. into x and y components as shown in Figs. 22-26e and f, we see that their y components cancel (because they have equal magnitudesand are in opposite directions). We also see that their x components have equal magnitudes and are in the same direction. Summing: Thus, to find the electric field set up by the rod, we nened sum (via integration) only the x components of the differential electric fields set up by all the differential elements of the rod. From Fig. 22-26f and Eq. 22-36, we can write the component `dE_(x)` set up by ds as `dE_(x)=dE cos theta=(1)/(4 pi epsilon_(0)) (lambda)/(r^(2)) cos theta ds."" (22-37)` Equation 22-37 has TWO variables, `theta` and s. Before we can integrate it, we must eliminate one variable. We do so by REPLACING ds, using the relation `ds=r d theta`, in which `d theta` is the angle at P that includes are length ds (Fig. 22-26g). With this REPLACEMENT, we can integrate Eq. 22-37 over the angle made by the rod at P, from `theta= -60^(@)` to `theta=60^(@)`, that will give us the field magnitude at P: `E= int dE_(x)= int_(-60^(@))^(60^(@)) (1)/(4pi epsilon_(0)) (lambda)/(r^(2)) cos theta r d theta` `=(lambda)/(4 pi epsilon_(0)r) int_(-60^(@))^(60^(@)) cos theta d theta = (lambda)/(4 pi epsilon_(0)r) [sin theta]_(-60^(@))^(60^(@))` `=(lambda)/(4pi epsilon_(0)r) [sin 60^(@)-sin(-60^(@))]=(1.73lambda)/(4pi epsilon_(0)r).""(22-38)` (If we had reversed the limits on the integration, we would have gotten the same result but with a minus sign. Since theintegration gives only the magnitude of `vecE`, we would then have discarded the minus sign.) Charge density: To evaluate `lambda`, we note that the full rod subtends an angle of `120^(@)` and so is one-third of a full circle. It arc length is then `2pi r//3`, and its linear charge density must be `lambda=("charge")/("length")=(Q)/(2pi r//3)=(0.477Q)/(r )` Substituting this into Eq. 22-23 and simplifying give us `E=((1.73)(0.477Q))/(4pi epsilon_(0)r^(2))=(0.83Q)/(4pi epsilon_(0)r^(2)). "" ` (Answer) The direction of `vecE` is toward the rod, along the axis of symmetry of the charge distribution. We can write `vecE` in unit-vector notation as `vecE=(0.83Q)/(4pi epsilon_(0)r^(2))hati`. |
|