Find the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is mu_1 and that between the bigger block and the ground is mu_2.

Find the acceleration of the block of mass M in the situation of figur

1.	Find the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is mu_1 and that between the bigger block and the ground is mu_2.
Answer» Solution :Let the acceleration of the block M is a towards rilght. So the block m MUST to down with an acceleration 2a. M it will also have acceleration a towards right. So it will EXPERIENCE two nertial forces as shown the free body diagram. From free body digram........1 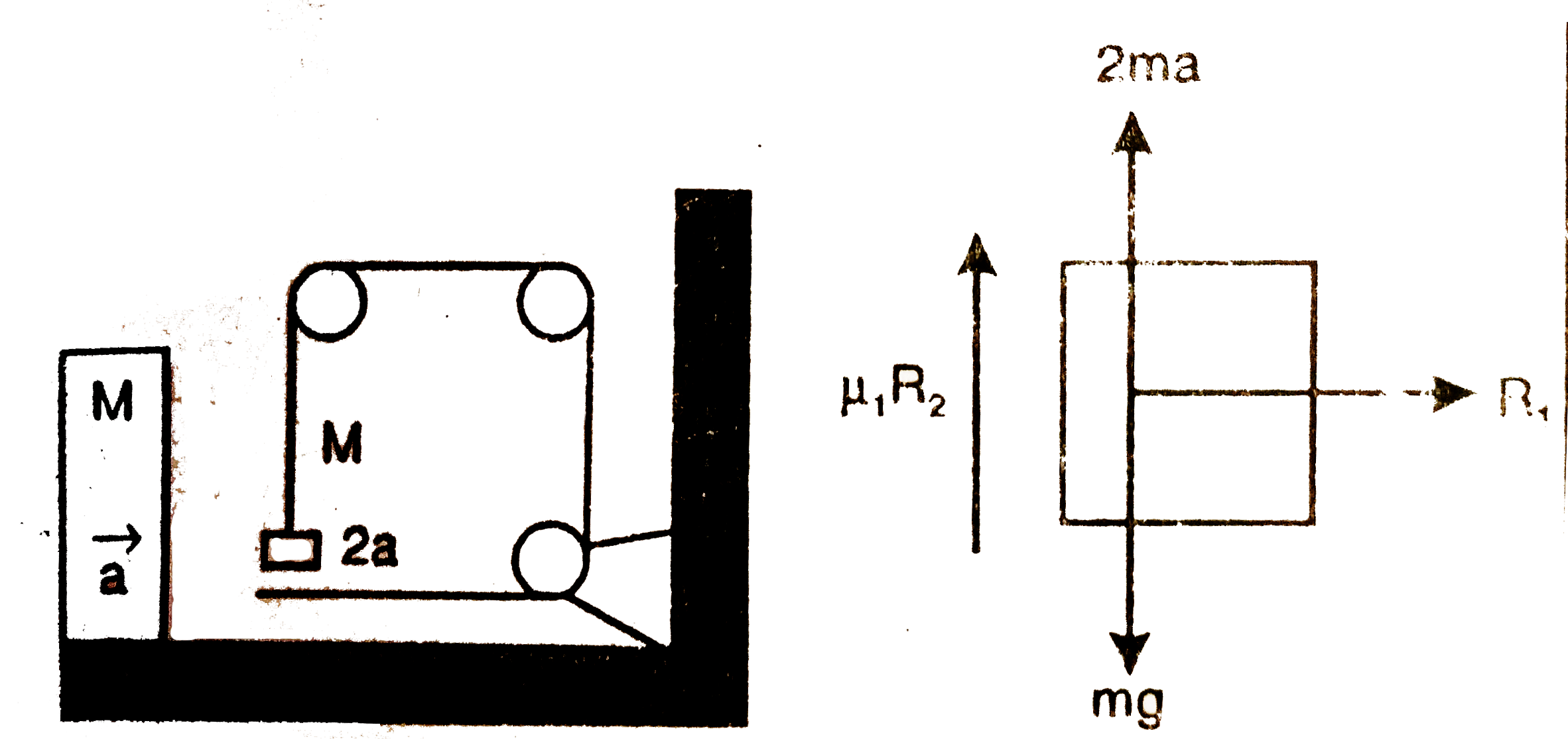`R_1-ma=0` `rarr R_1=ma`..........i Again, `2ma+T-Mg+mu_1R_1=0` `rarr T=Mg-(2+mu_1)ma`.........II From free body diagram -2, `T+mu_1R_1+Mg-R_2=0` Putting the VALUE of `R_1` from i `R_2=T+mu_1 ma+mg` Putting teh value of T from ii, `R_2=(Mg-2ma-mu_1ma)=mu_1ma+Mg+mg` R_2=Mg+mg-2ma`.....iii Again fromn the free body diagram 2, `T+T-R-Ma-mu_2R_2=0` `rarr 2T-Ma-ma-mu_2(Mg+mg-2ma)=0` Putting the values of `R_1 and R_2` from i and iii `2T=(M+m)a+mu_2(Mg+mg-2ma)`....iv From EQUATION ii and iv we have `2T=2mg-2(2+mu_1)ma` `=(M+m)a+mu_2(Mg+mg-2ma)` `rarr 2mg-mu_2(M+m)g` `=a[M+m-2mu_2m+4m+2mu_1m]` `rarr a=([2m-m_2(M+m)]g)/(M+m[5+2(mu_1-mu_2)])`