Find the direction in which a straight line must be drawn through the point (-1,2) so that its point of intersection with the line x+y=4 may be at a distance of 3 units from this point.

Find the direction in which a straight line must be drawn through the

1.	Find the direction in which a straight line must be drawn through the point (-1,2) so that its point of intersection with the line x+y=4 may be at a distance of 3 units from this point.
Answer» Solution :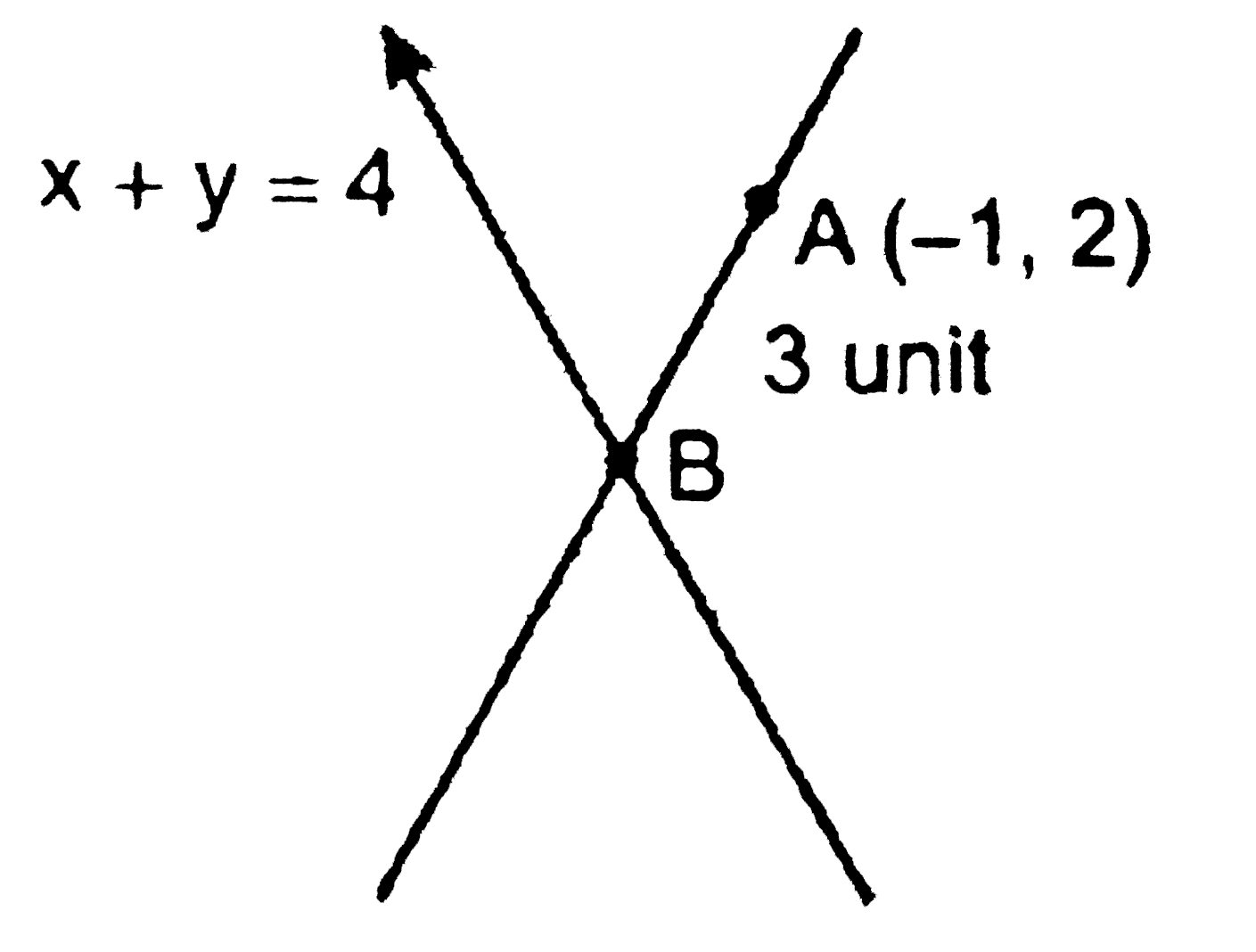 Let the slope of REQUIRED line PASSING through the point `(-1,2)` is `m`. `,.` Equation of line is, `y-2=m(x+1)` `impliesmx-y=-2-m`…….`(1)` Given line is, `x+y=4`……..`(2)` Solving we get `x=(2-m)/(m+1)` and `y=(5m+2)/(m+1)` `:.` Point of intersection is , `B=((2-m)/(m+1),(5m+2)/(m+1))` Given that `AB=3` units `impliessqrt(((2-m)/(m+1)+1)^(2)+((5m+2)/(m+1)-2)^(2))=3` `impliessqrt(((3)^(2)+(3m)^(2))/((m+1)^(2)))=3` `implies 3^(2)+9m^(2)=9(m+1)^(2)` `implies 9+9m^(2)=9m^(2)+18m+9` `implies 4m+18m=0` `impliesm=0` Now, `m=0` then `TAN theta=0impliestheta=0^(@)` `implies` Line is parallel to `x`-axis.