For the final challenge, Bowser asks, “For which integers n, does there exist a shape which can be tiled using 2 × 1dominoes in exactly n different ways?”

For the final challenge, Bowser asks, “For which integers n, does th

1.	For the final challenge, Bowser asks, “For which integers n, does there exist a shape which can be tiled using 2 × 1dominoes in exactly n different ways?”
Answer» All NATURAL Numbers n is power of 2 n is an even number n = 2,4 Solution :For n = 1, a `2× 1` rectangle can be tiled by a domino in exactly one way. Forn = 2, the following shape can be tiled in exactly two ways. Note that thereis a `2 × 1` rectangular hole in the middle which is not part of the shape. This CONSTRUCTION can actually be generalised to any n. For n = 5 we havethe following shape (with four holes). 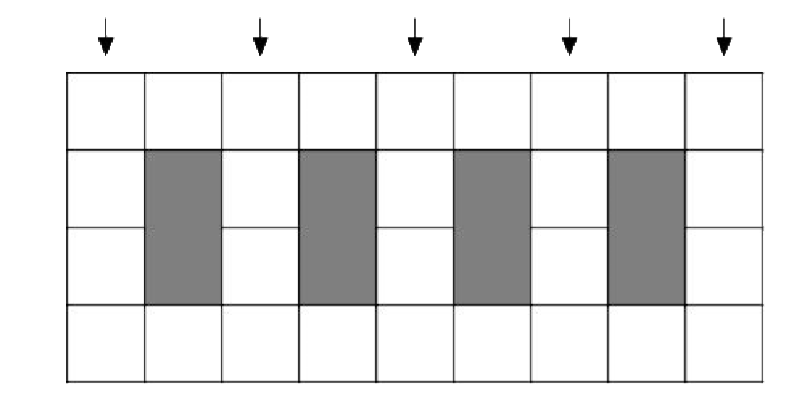Call a column strong if it has two vertical dominoes. Out of the five columnsindicated, at least one must be strong. But as soon as we CHOOSE a strongcolumn, the tiling is forced and no other columns can also be strong. Forexample, if the fourth column is strong, the following tiling is forced. 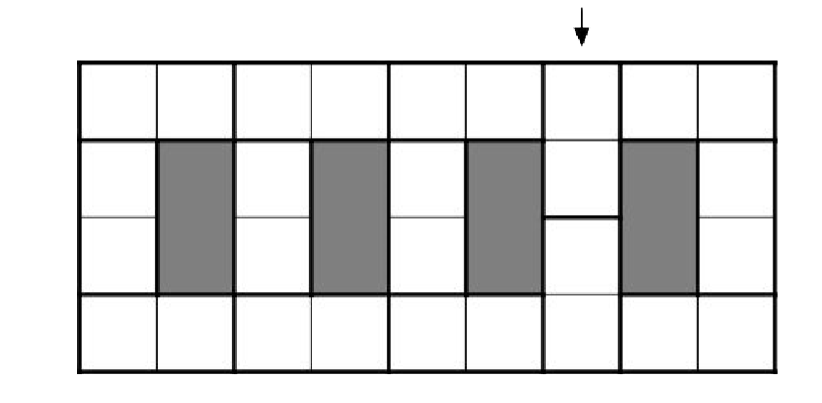Since there were five POSSIBLE choices of strong columns, there are exactlyfive ways to tile the shape. By similar arguments, for all natural numbers n,there exists a shape which can be tiled by dominoes in exactly n ways.

Discussion

No Comment Found

Related InterviewSolutions

P (-2,-1) and (0,-3) are the limiting points of a coaxial system of whichC -= x^(2) + y^(2)+ 5x + y + 4 = 0is a member. The circleS -= x^(2) + y^(2) - 4x - 2y - 15 = 0is orthogonal to the circle C . The point where the polar of P cuts the circle S is
Which of the following is/are discontinous at x = 1 ?
Write Minors and Cofactors of the elments of following determinants : |{:(1,0,4),(3,5,-1),(0,1,2):}|
The vertex of the parabola (y-1)^2 =8 (x-1) is at the centre of a circle and the parabola cuts that circle atthe ends of its latusrectum. Then the equation of that circle is
{{:(5x-3y=10),(6y=kx-42):} In the system of linear equations above, k represents a constant. If the system of equations has no solution, what is the value of 2k?
f(x) ={{:(1-sqrt(1-x^(2)),if -1lexle1),(1+ log ""(1)/(x), if xgt1):}
Given that alpha, beta, gamma, delta are in a geometric progression. If alpha, beta are the roots of x^(2)-x+p=0 " and "gamma, delta are the roots of x^(2)-4x+q=0, where p and q are integers, then the ordered pair (p, q) =
A poor , frustrated artist named Fresco created a plan to make money. He collected trash, repurposed it into sculptures, then asked various celebrities to write and paint on these trash objects, which he then sold on his own as modern high art. The chart below separately showsthe cost and revenue of his plan. The linear cost function, C(x) , represents the total money spent to make and market the art , while the linear revenue function, R(x) , shows the amount of money he has made in sculpture sales. Fresco initially spent money promoting the project in the media . He also had to pay the celebrities to participate . After 6 months , Fresco had created and sold x number of trash sculptures and finally broke even : he hadn't made or lost any money . How many sculptures did Fresco sell in his first 6 months of the project ?
A poor , frustrated artist named Fresco created a plan to make money. He collected trash, repurposed it into sculptures, then asked various celebrities to write and paint on these trash objects, which he then sold on his own as modern high art. The chart below separately showsthe cost and revenue of his plan. The linear cost function, C(x) , represents the total money spent to make and market the art , while the linear revenue function, R(x) , shows the amount of money he has made in sculpture sales. The cost function in the chart is determined by a constant production cost per sculpture - in this case, the amount Fresco pays each celebrity to participate - as well as a fixed cost , or the initial cost of promoting the project . What is the fixed cost of Fresco's trash sculpture project ?
An ellipse is incribed in a rectangle and if the angle between the diagonals is tan ^(-1)2sqrt2then e=

For the final challenge, Bowser asks, “For which integers n, does there exist a shape which can be tiled using 2 × 1dominoes in exactly n different ways?”

Discussion

No Comment Found

Related InterviewSolutions

Reply to Comment