1.

From the following table, calculate the coefficient of correlation by Karl Pearson's method: Arithmetic means of X and Y series are 6 and 8 respectively.

Answer» <html><body><p></p>Solution :Let us first and <a href="https://interviewquestions.tuteehub.com/tag/missing-1098377" style="font-weight:bold;" target="_blank" title="Click to know more about MISSING">MISSING</a> value of Y and let us denote it by a . <br/> `bar(Y)=(sumY)/(N)=(9+11+a+8+7)/(5)=(35+a)/(5)` <br/> `implies 8=(35+a)/(5)` <br/> `:. 35+a=40` <br/> `implies a=5` <br/> Thus, the complete <a href="https://interviewquestions.tuteehub.com/tag/series-1201802" style="font-weight:bold;" target="_blank" title="Click to know more about SERIES">SERIES</a> is : <br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/TRJ_ECO_XI_C12_S01_011_S01.png" width="80%"/> <br/> Now we find the coefficient of correlation. 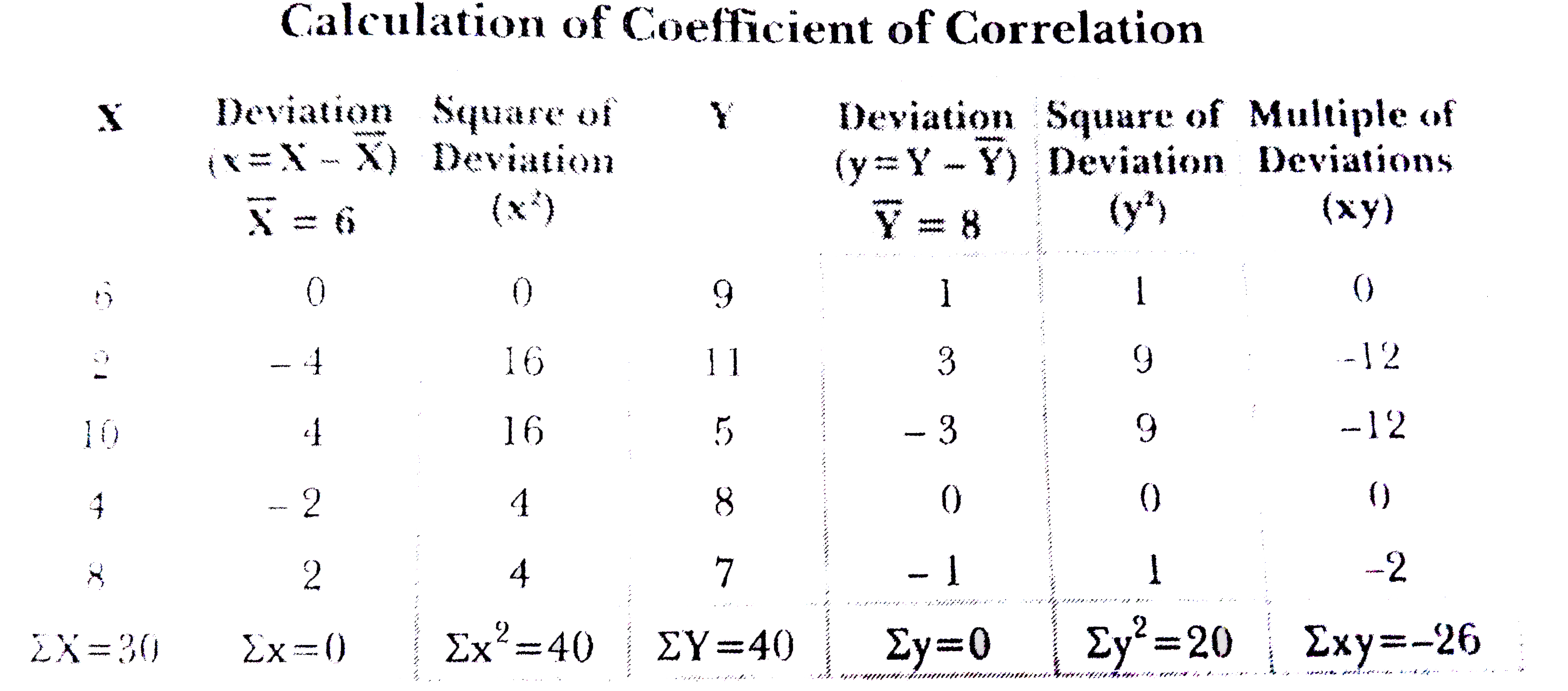<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/TRJ_ECO_XI_C12_S01_011_S02.png" width="80%"/> <br/> `<a href="https://interviewquestions.tuteehub.com/tag/r-611811" style="font-weight:bold;" target="_blank" title="Click to know more about R">R</a>=(sumxy)/(sqrt(<a href="https://interviewquestions.tuteehub.com/tag/sumx-3819684" style="font-weight:bold;" target="_blank" title="Click to know more about SUMX">SUMX</a>^(2)xxsumy^(2)))` <br/> The table shows that ` sumxy=-26,sum x^(2)=40,sumy^(2)=<a href="https://interviewquestions.tuteehub.com/tag/20-287209" style="font-weight:bold;" target="_blank" title="Click to know more about 20">20</a>` <br/>Substituting the values, we get <br/> `r=(-26)/(sqrt(10xx20))` <br/> `=(-26)/(sqrt(800))=(-26)/(28.28)` <br/> `=-0.92` <br/> Coefficient of Correlation (r)= -0.92</body></html>


Discussion

No Comment Found

Related InterviewSolutions