Saved Bookmarks
| 1. |
In the figure a truck is moving on a horizontal surface with acceleration a. Two blocks of equal masses m are supported on the truck as shown in figure. Given that when the block at the top surface is just about to slide, other block remains hanging at 30^(@) from the vertical. In this system. |
|
Answer» `a=(g)/(sqrt(3))` `T cos 30^(@)=mg …….(2)` 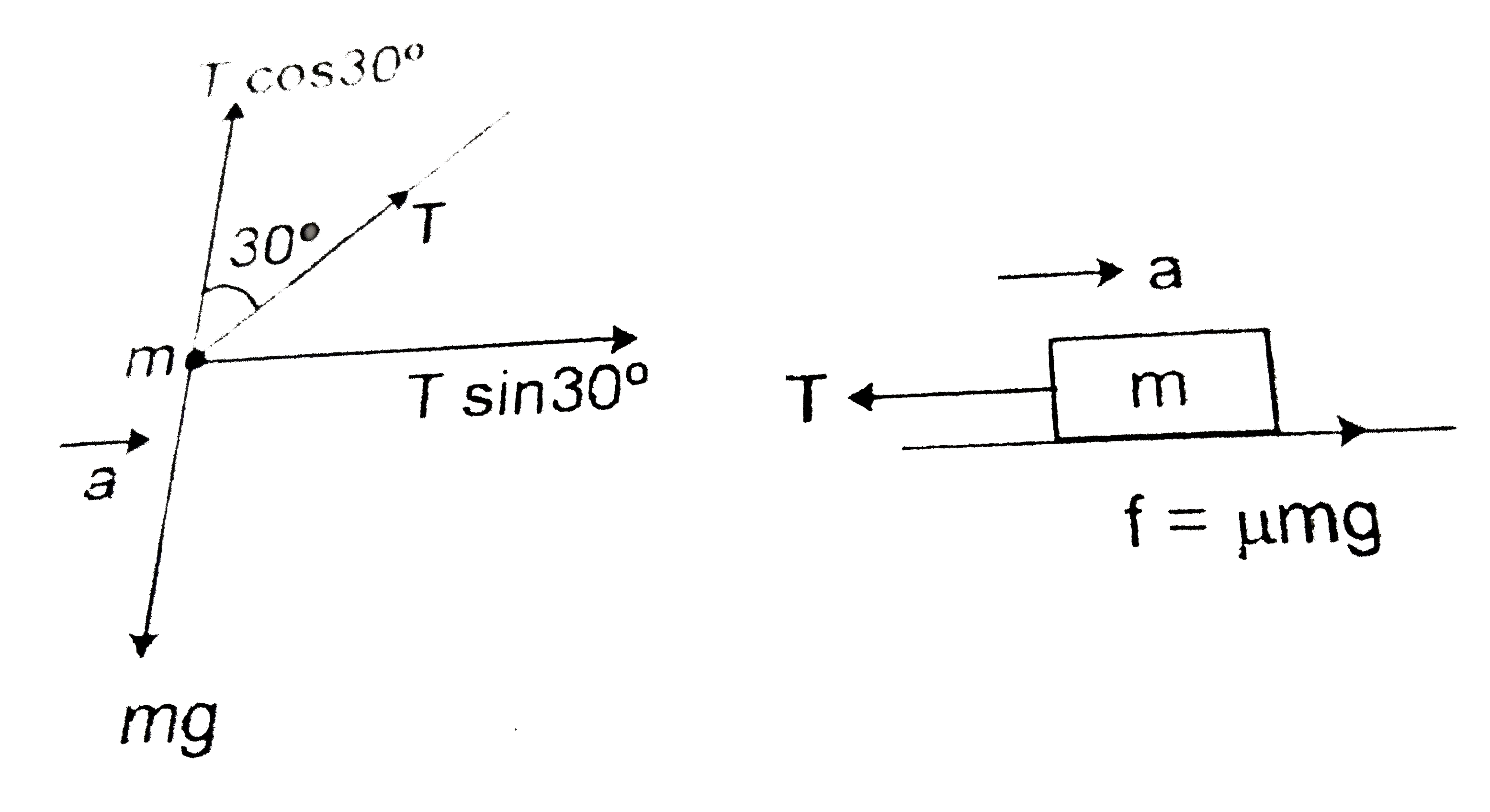 dividing equation `(1)` by equation `(2)` `tan 30^(@)=(a)/(g)` `rArr a=gtan 30^(@)` `rArr a=(g)/(sqrt(3))` Ans. From `(2)T=(mg)/(cos 30^(@))=(2MG)/(sqrt(3))`Ans. and `mu mg-T=ma` `rArr mu mg=T+ma=(2mg)/(sqrt(3))+ma` `=(2mg)/(sqrt(3))+(mg)/(sqrt(3))` `rArr mumg=(3MG)/(sqrt(3))=sqrt(3)mg` `=mu=sqrt(3) Ans.` |
|
Discussion
No Comment Found
Related InterviewSolutions
- What is uniform velocity
- Derive the speed time equation by calculas method
- 9×2y - 24x^2 +16y^3.factorise?
- Give me tips for preparation of physics??
- Advantage of friction
- Derivation of equation of Newton\'s Second Law of Motion that is F=ma
- Equation of projectile?
- Unit of Permeability
- Difference between vectr and scalar
- what is centripetal force ?