InterviewSolution
Saved Bookmarks
| 1. |
Let A(z_(1)), B(z_(2)), C(z_(3) and D(z_(4)) be the vertices of a trepezium in an Argand plane such that AB||CD Let |z_(1)-z_(2)|=4, |z_(3),z_(4)|=10 and the diagonals AC and BD intersects at P. It is given that Arg((z_(4)-z_(2))/(z_(3)-z_(1)))=(pi)/2 and Arg((z_(3)-z_(2))/(z_(4)-z_(1)))=(pi)/4 Which of the following option(s) is/are incorrect? |
|
Answer» Value of `|CP-DP|` is equal to `10/(sqrt(21))` `BP=2Y` then `CP=5x, DP=5y` AREA of trapezium `ABCD=49/2xy` `TAN alpha=(2x)/(5y), tan beta =(2y)/(2x)` also `alpha+beta=45^(@)` `impliesxy=10/21(x^(2)+y^(2))` Also `AB^(2)=AP^(2)+BP^(2)impliesx^(2)+y^(2)=4impliesxy=40/21` `Ar(DeltaPCD)=5xy` 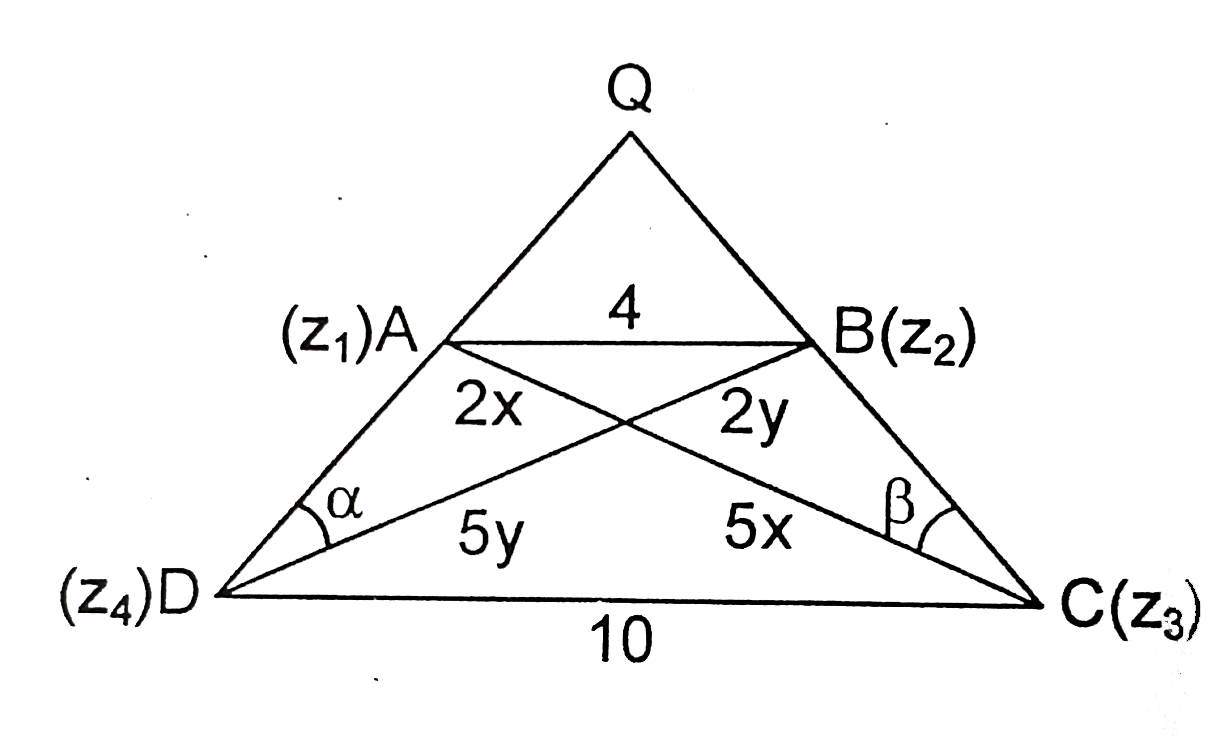
|
|