| 1. |
Let T(n) be the number of different binary search trees on n distinct elements.Then , where x is(A) n-k+1(B) n-k(C) n-k-1(D) n-k-2 |
|
Answer» Answer: (B) Explanation: The idea is to make a key root, put (k-1) keys in one subtree and remaining n-k keys in other subtree. A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −
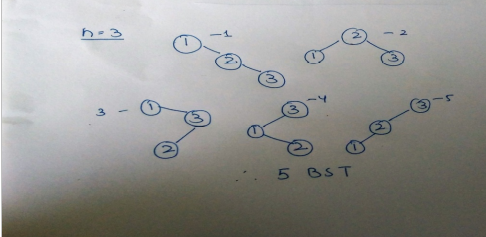
Now construction binary search trees from n distinct number- If n=3 We have 5 possibilities. Keeping each number first as root and then arranging the remaining 2 numbers as in case of n=2. |
|
Discussion
No Comment Found
Related InterviewSolutions
- Consider the following assembly language program for a hypothetical processor. A, B, and C are 8 bit registers. The meanings of various instructions are shown as comments.MOV B, # 0; B ← 0MOV C, # 8; C ← 8Z :CMP C, # 0; compare C with 0JZX; jump to X if zero flag is setSUB C, # 1; C ← C – 1RRC A, # 1; right rotate A through carry by one bit. Thus:; if the initial values of A and the carry flag are a7…a0 and; c0 respectively, their values after the execution of this; instruction will be c0a7…a1 and a0 respectively.JC Y; jump to Y if carry flag is setJMP Z; jump to ZY :ADD B, # 1; B ← B + 1JMP Z; jump to ZX :(A) the number of 0 bits in A0(B) the number of 1 bits in A0(C) A0(D) 8
- Consider the following three claims1. (n + k)m = Θ(nm), where k and m are constants2. 2n + 1 = O(2n)3. 22n + 1 = O(2n) Which of these claims are correct ?(A) 1 and 2(B) 1 and 3(C) 2 and 3(D) 1, 2, and 3
- Let G = (V, E) be an undirected graph with a subgraph G1 = (V1, El). Weights are assigned to edges of G as follows : A single-source shortest path algorithm is executed on the weighted graph (V, E, w) with an arbitrary vertex ν1 of V1 as the source. Which of the following can always be inferred from the path costs computed?(A) The number of edges in the shortest paths from ν1 to all vertices of G(B) G1 is connected(C) V1 forms a clique in G(D) G1 is a tree
- The following are the starting and ending times of activities A, B, C, D, E, F, G and H respectively in chronological order: “asbscsaedsceesfsbedegseefehsgehe”Here,xs denotes the starting time and xe denotes the ending time of activity X. W need to schedule the activities in a set of rooms available to us. An activity can be scheduled in a room only if the room is reserved for the activity for its entire duration. What is the minimum number of rooms required ?(A) 3(B) 4(C) 5(D) 6
- The cube root of a natural number n is defined as the largest natural number m such that m3 ≤ n. The complexity of computing the cube root of n (n is represented in binary notation) is:(A) O(n) but not O(n0.5)(B) O(n0.5) but not O((log n)k) for any constant k > 0(C) O((log n)k) for some constant k > 0, but not O ((log log n)m) for any constant m > 0(D) O((log log n)m) for some constant k > 0.5, but not O((log log n)0.5)
- Let G (V, E) be a directed graph with n vertices. A path from vi to vj in G is sequence of vertices (vi, vi+1, ……., vj) such that (vk, vk+1) ∈ E for all k in i through j – 1. A simple path is a path in which no vertex appears more than once.Let A be an n x n array initialized as follow Consider the following algorithm.for i = 1 to n for j = 1 to n for k = 1 to n A [j , k] = max (A[j, k] (A[j, i] + A [i, k]); Which of the following statements is necessarily true for all j and k after terminal of the above algorithm ?(A) A[j, k] ≤ n(B) If A[j, k] ≥ n – 1, then G has a Hamiltonian cycle(C) If there exists a path from j to k, A[j, k] contains the longest path lens from j to k(D) If there exists a path from j to k, every simple path from j to k contain most A[j, k] edges
- What is the weight of a minimum spanning tree of the following graph ?(A) 29(B) 31(C) 38(D) 41
- In a permutation a1…..an of n distinct integers, an inversion is a pair (ai, aj) such that i aj. If all permutations are equally likely, what is the expected number of inversions in a randomly chosen permutation of 1…..n ?(A) n(n – 1)/2(B) n(n – 1)/4(C) n(n + 1)/4(D) 2n[log2 n]
- Consider the following 2-3-4 tree (i.e., B-tree with a minimum degree of two) in which each data item is a letter. The usual alphabetical ordering of letters is used in constructing the tree.What is the result of inserting G in the above tree ?A) B) C) D) None of the above(A) A(B) B(C) C(D) D
- Let S be a stack of size n ≥ 1. Starting with the empty stack, suppose we push the first n natural numbers in sequence, and then perform n pop operations. Assume that Push and pop operation take X seconds each, and Y seconds elapse between the end of one such stack operation and the start of the next operation. For m ≥ 1, define the stack-life of m as the time elapsed from the end of Push(m) to the start of the pop operation that removes m from S. The average stack-life of an element of this stack is(A) n (X + Y)(B) 3Y + 2X(C) n (X + Y) – X(D) Y + 2X