InterviewSolution
Saved Bookmarks
| 1. |
The number of values of x in the interval [0,5pi] satisfying the equation. 3sin^(2)x -7sinx + 2=0 is- |
|
Answer» 0 `rArr (3sinx-1)(sinx-2)=0` `therefore sinx ne 2` `rArr sinx=1/3 =sinalpha` (SAY) Where `alpha` is the least positive VALUE of x such that `sinalpha=1/3` 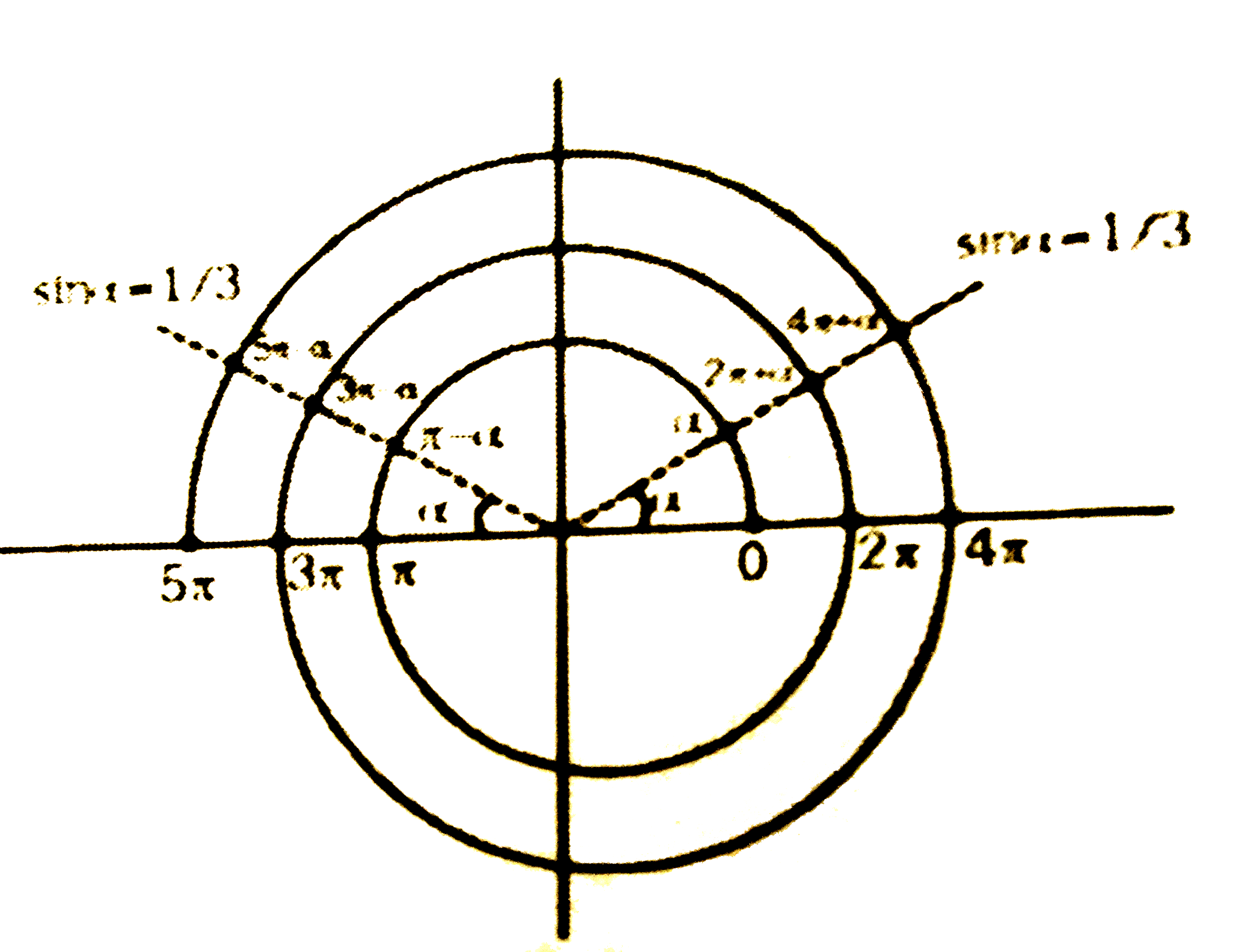 Clearly, `0 lt alpha lt pi/2`. We get the solution, `x=alpha, pi-alpha, 2pi+alpha, 4PI + alpha` and `5pi- alpha` Hence total six VALUES in `[0,5pi]` Ans. |
|