1.

The spring has a force constant k. The pulley is light and smooth while the spring and string are light figure. If the block of mass m slightly displaced vertically and released, find the period of verticall oscillations.

Answer» <html><body><p></p>Solution :Let `x_(<a href="https://interviewquestions.tuteehub.com/tag/0-251616" style="font-weight:bold;" target="_blank" title="Click to know more about 0">0</a>)` be the extension in the spring in <a href="https://interviewquestions.tuteehub.com/tag/equilibrium-974342" style="font-weight:bold;" target="_blank" title="Click to know more about EQUILIBRIUM">EQUILIBRIUM</a> position and `F_(0)` be the tension in the spring. Then <br/> `F_(0)=kx_(0)` <br/> If `T_(0)` is the tension in the string, then <br/> `T_(0)=mf or 2T_(0)=F_(0)=kx_(0)`…(i) <br/> Let mass m be pulled downward through distnace x, then tension in spring and string be F and T respectively. <br/> Now `F=2T=k(x_(0)=x//2)=kx_(0)<a href="https://interviewquestions.tuteehub.com/tag/kx-1064991" style="font-weight:bold;" target="_blank" title="Click to know more about KX">KX</a>//2` <br/> or `2T=2T_(0)+kx//2`[from (i)] <br/> or `T-T_(0)=kx//4` <br/> Restoring force on the mass m is <br/> `f=T-mg=T-T_(0)=kx//4`...(ii) <br/> From (ii) , `fpropx and f` is a restoring force, therefore, if mass m is left <a href="https://interviewquestions.tuteehub.com/tag/free-465311" style="font-weight:bold;" target="_blank" title="Click to know more about FREE">FREE</a>, it will execute SHM. <br/> Here, spring factore`=k//4,` inertia factore `=`m. <br/> <a href="https://interviewquestions.tuteehub.com/tag/time-19467" style="font-weight:bold;" target="_blank" title="Click to know more about TIME">TIME</a> period, `T=2pisqrt((m)/(k//4))=4pisqrt((m)/(k))` 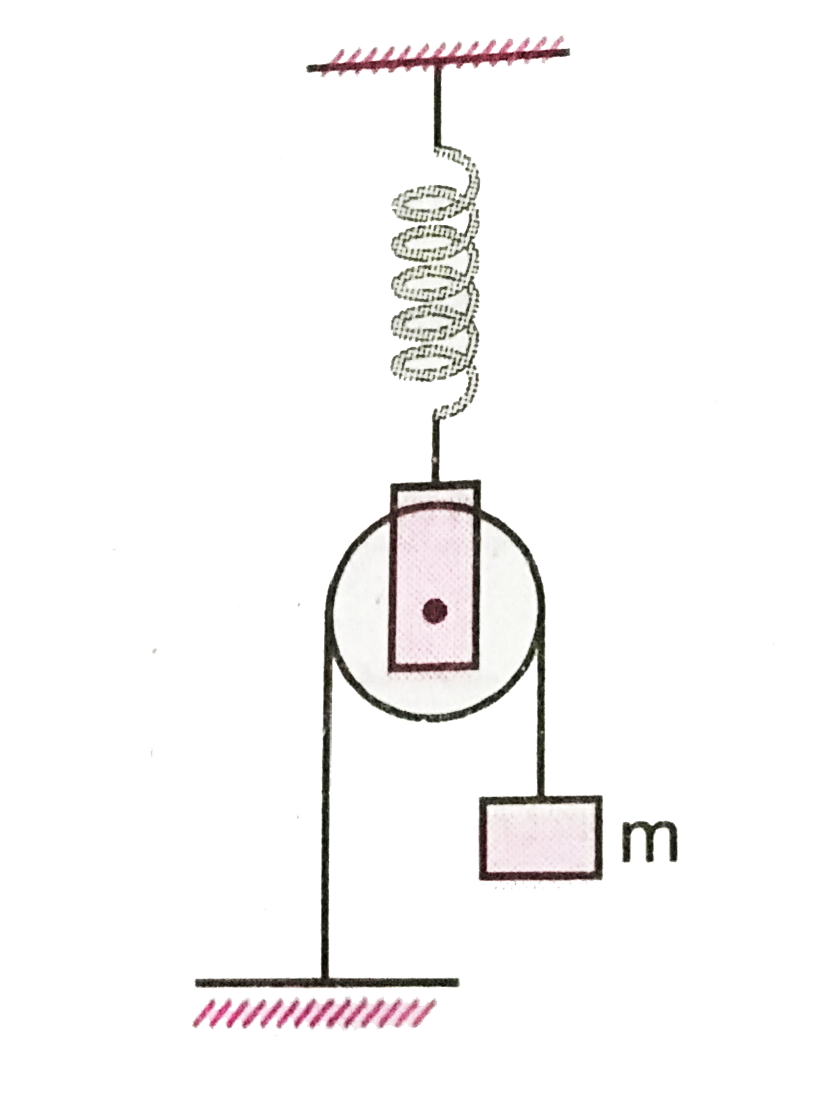<br/> <img src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XI_V02_C10_S01_413_S01.png" width="80%"/></body></html>


Discussion

No Comment Found

Related InterviewSolutions