Saved Bookmarks
| 1. |
The yield of wheat and rice per acre for 10 districts of a state is as under: Calculate for each crop, (i) Range (ii) Q.D. (iii) Mean Deviation about Mean (iv) Mean deviation about Median (v) Standard Deviation (vi) Which crop has greater variations? (vii) Compare the values of different measures for each crop. |
|
Answer» Solution :[ Case of Wheat: Firstly arrange the data in ascending order: 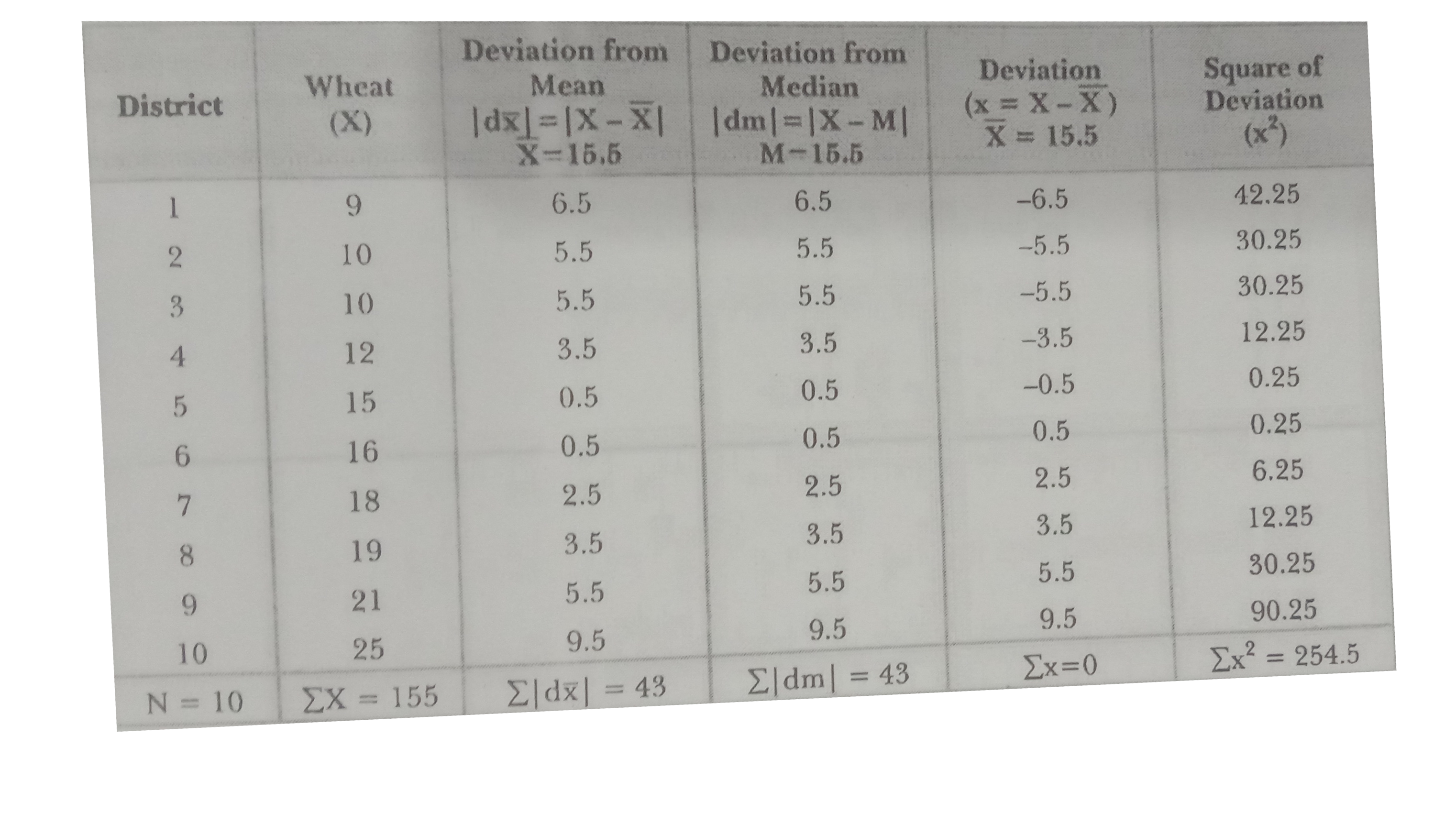 (i) Range (R )=H-L Here, H=25, L=9 `:. ""` R=25-9=16 (ii) `"" Q_(1)`=Size of `((N+1)/(4))th" item"` =Size of `((10+1)/(4))th " item"` =Size of 2.75th item =Size of 2nd item`+(3)/(4)("Size of 3rd item"-"Size of 2nd item")` `=10+(3)/(4)(10-10)` =10+0=10 `Q_(3)="Size of"3((N+1)/(4))th " item"` `="Size of " 3((10+1)/(4))th item"` =Size of 8.25th item =Size of 8TH item `+(1)/(4)("Size of 9th item"-"Size of 8th item")` `=19+(1)/(4)(21-19)=19+(2)/(4)=19.5` Quartile Deviation`=(Q_(3)-Q_(1))/(2)=(19.5-10)/(2)=(9.5)/(2)=4.75` (iii) Mean `(barX)=(sumX)/(N)=(155)/(10)=15.5` Mean Deviation from Mean `(MD_(barX))=(sum|dx|)/(N)=(43)/(10)=4.3` (iv) Median (M)=Size of `((N+1)/(2))th" item"` =Size of `((10+1)/(2))th " item"`=Size of 5.5th item `="Size of 5th item"+"Size of 5th item")/(2)` `=(15+16)/(2)=(31)/(2)=15.5` Mean Deviation from Median `(MD_(m))=(sum|dm|)/(N)=(43)/(10)=4.3` (v) Standard Deviation `(SIGMA)=sqrt((sumx^(2))/(N))=sqrt((254.5)/(10))=sqrt(25.45)=5.04` (vi) Coefficient of Variation (CV)`=(sigma)/(barX)XX100=(5.04)/(15.5)xx100=32.52`] [Note: Students are advised to repeat this exercise using data for the rice crop. To assess the degree of variation, COMPARE CV for the two cases.] |
|