InterviewSolution
Saved Bookmarks
| 1. |
There are factories located one at place P and other at place Q from which a certin commodity is to be delivered to each of three depot situated at A,B and C. The weekly requirement of the depots are respectively 5,5 and 4 units of the commodity while the production capacity of the factories P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below. How many units should be transported from each factory to each depot in order that the transportation cost is minimum. Also find the minimum transportation cost. |
|
Answer» <P> Solution :Let `x` and `y` units of commodity be TRANSPORTED from the factory `P` to depots A and B respectively. Thus `(8-x-y)` units will be transported from `P` to depot `C`.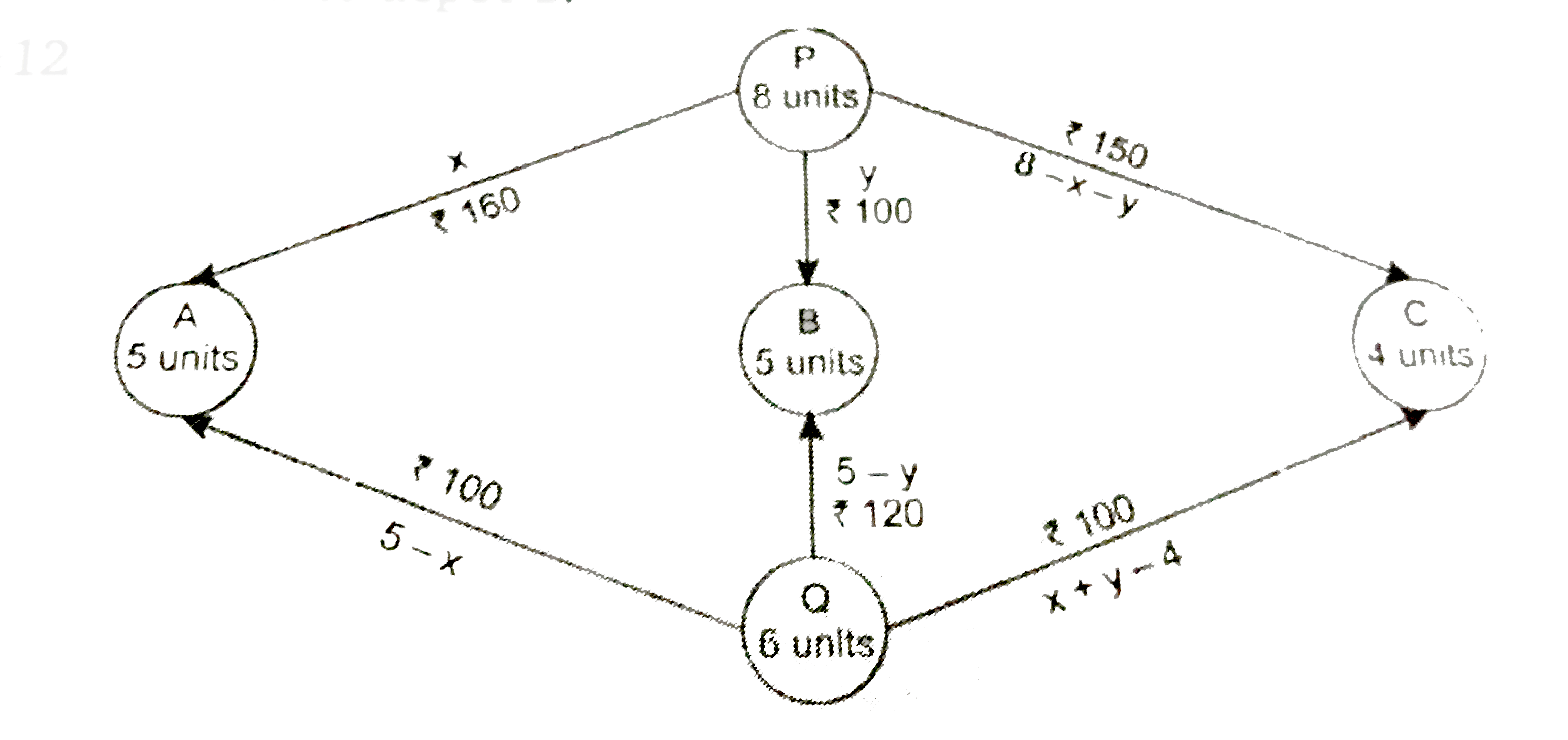 Now the number of units transported from `Q` factory to the depots A,B and C will be `5-x,5-y` and `x+y-4` respectively as shown in the diagram. Therefore `xge0` `yge0` `8-x-yge0impliesx+yle8` `5-xge0impliesxle5` `5-tge0impliesyle5` `x+y-4ge0impliesx+yge4` and transportation cost `z=160x+100y+150(8-x-y)+100(5-x)` `+120(5-y)+100(x+y-4)` `=160x+100y+1200-150x-150y+500` `-100x+600-120y+100x+100y-400` `=10x-70y+1900` Thus the linear PROGRAMMING problem is Minimize `z=10x-70y+1900` Subject to: `xge0` `yge0` `XLE5` `yle5` `x+yle8` `x+yge4` Draw the graph of corresponding equations and obtain the feasible region and SHADE it. The convex region is ABCDEF whose vertices are `A(4,0),B(5,0),C(5,3),D(3,5),E(0,5)` and `F(0,4)`. We will find the value of `z` at each of these vertices. 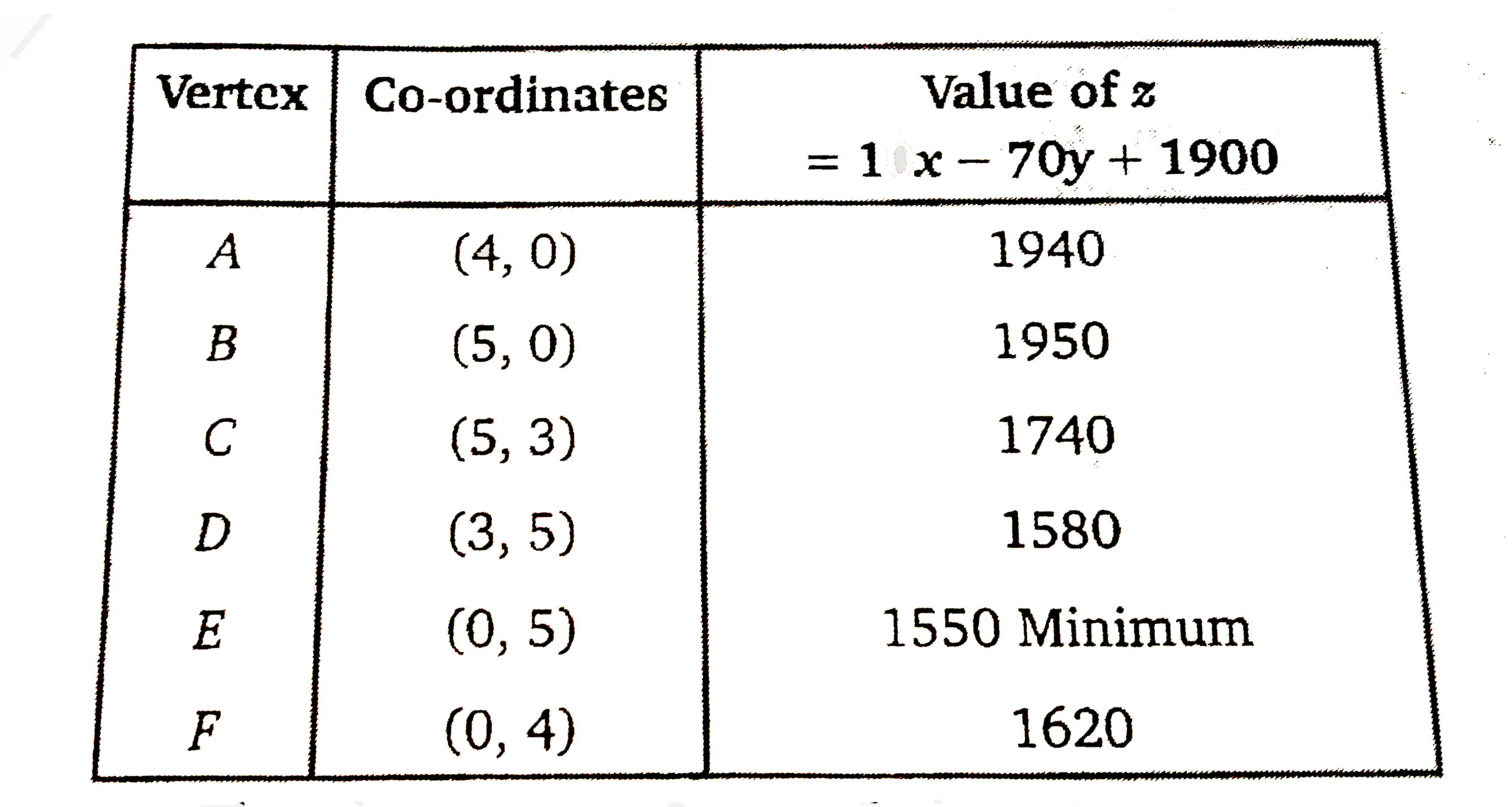 Therefore at `x=0,y=5` the minimum cost is Rs. 1551. 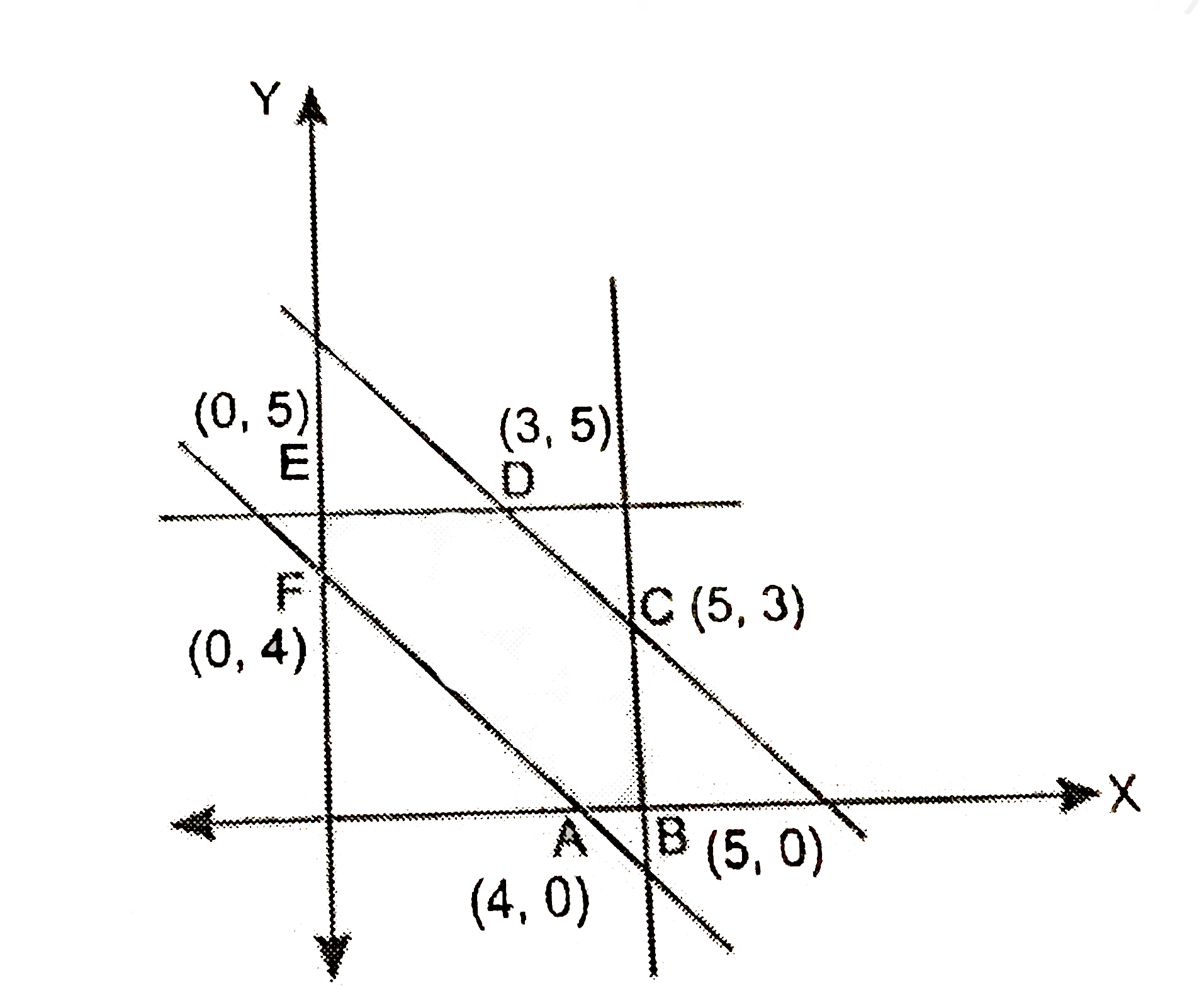 Therefore for minimum cost of transportation we will transport 0,5 and 3 units from `P` to A,B and Crespectively and 5,0 and 1 unit from `Q` to A,B and C respectively. |
|