Three particles, each of mass m are placed at the vertices of an equilateral triangle of side a. What are the gravitation field and gravitational potential at the centroid of the triangle.

Three particles, each of mass m are placed at the vertices of an equil

1.	Three particles, each of mass m are placed at the vertices of an equilateral triangle of side a. What are the gravitation field and gravitational potential at the centroid of the triangle.
Answer» Solution :Refer to Fig. `O` is the centriod of triangle `ABC`, where `OA = (2)/(3) AD = (2)/(3) (AB sin 60^(@))` `= (2)/(3) xx a xx (sqrt(3))/(2) = (a)/(sqrt(3))` Thus, `OA = OB = OC = (a)/(sqrt(3))` 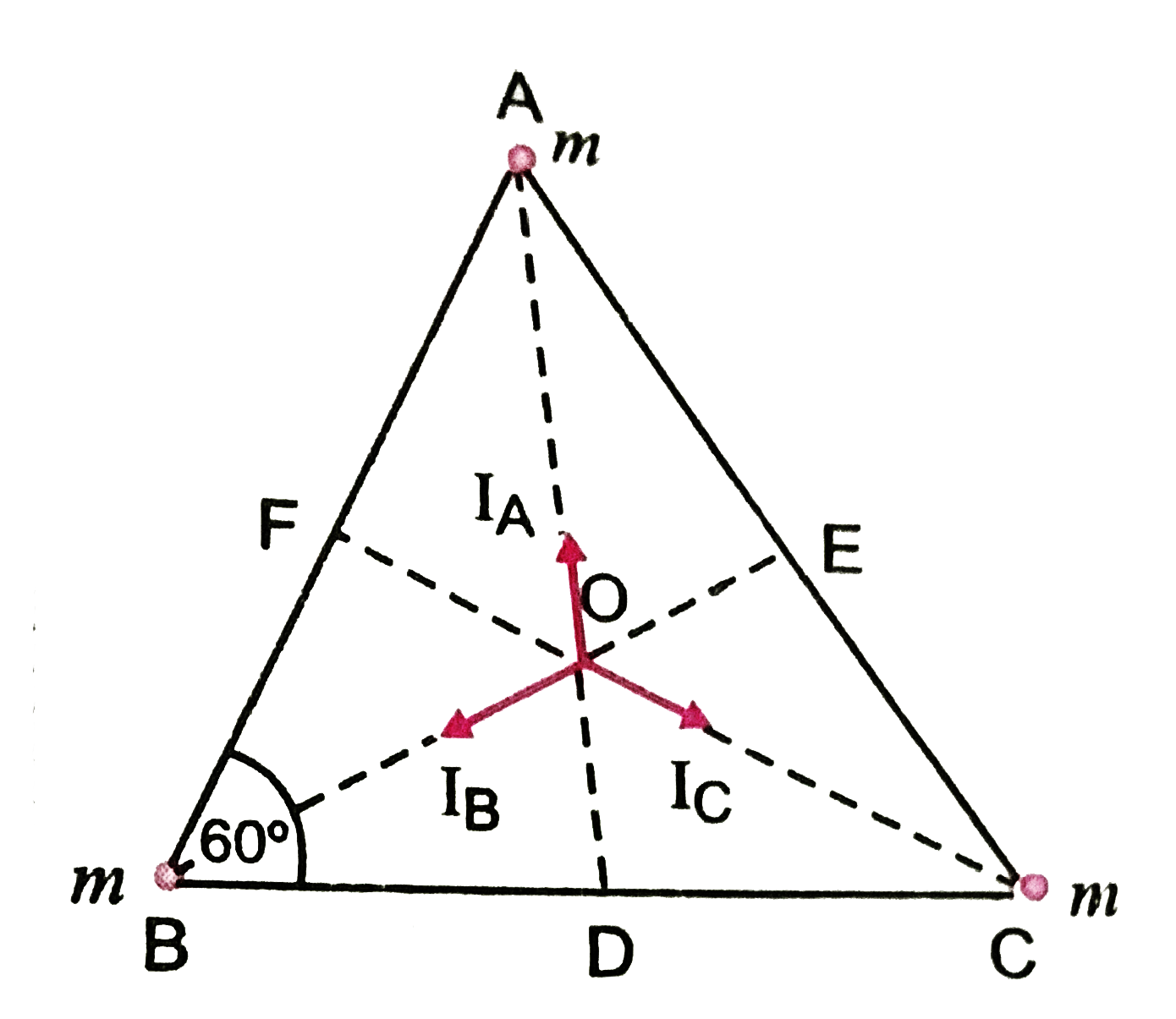The gravitational intensity at `O` DUE to mass `m` at `A` is, `I_(A) = (Gm)/((OA)^(2)) = (Gm)/((a//sqrt(3))^(2))` along `OA`. SIMILARLY the gravitational intensity at `O` due to mass `m` at `B` is, `I_(B) = (Gm)/((OB)^(2)) = (Gm)/((a//sqrt(3))^(2))` along `OB`. and gravitational intensity at `O` due to mass `m` at `C` is, `I_(C) = (Gm)/((OC)^(2)) = (Gm)/((a//sqrt(3))^(2))` along `OC`. As `I_(A),I_(B)` and `I_(C)` are EQUAL in magnitude and equally inclined to each other, the resultant gravitational intensity at `O` is zero. gravitational potential at `O` due to masses at `A,B` and `C` is `V = - (Gm)/(OA) + (-(Gm)/(OB)) + (-(Gm)/(OC))` `= - (3 Gm)/(OA) = (-3 Gm)/(a//sqrt(3)) = (-3 sqrt(3) Gm)/(a)`