InterviewSolution
Saved Bookmarks
| 1. |
Two tangents are drawn from any point P on a given line L=0 to a given circle S=0, if these tangents touch the circle at point A and B, then locus of the circumcentre the DeltaPAB will be |
|
Answer» A pair of straight lines 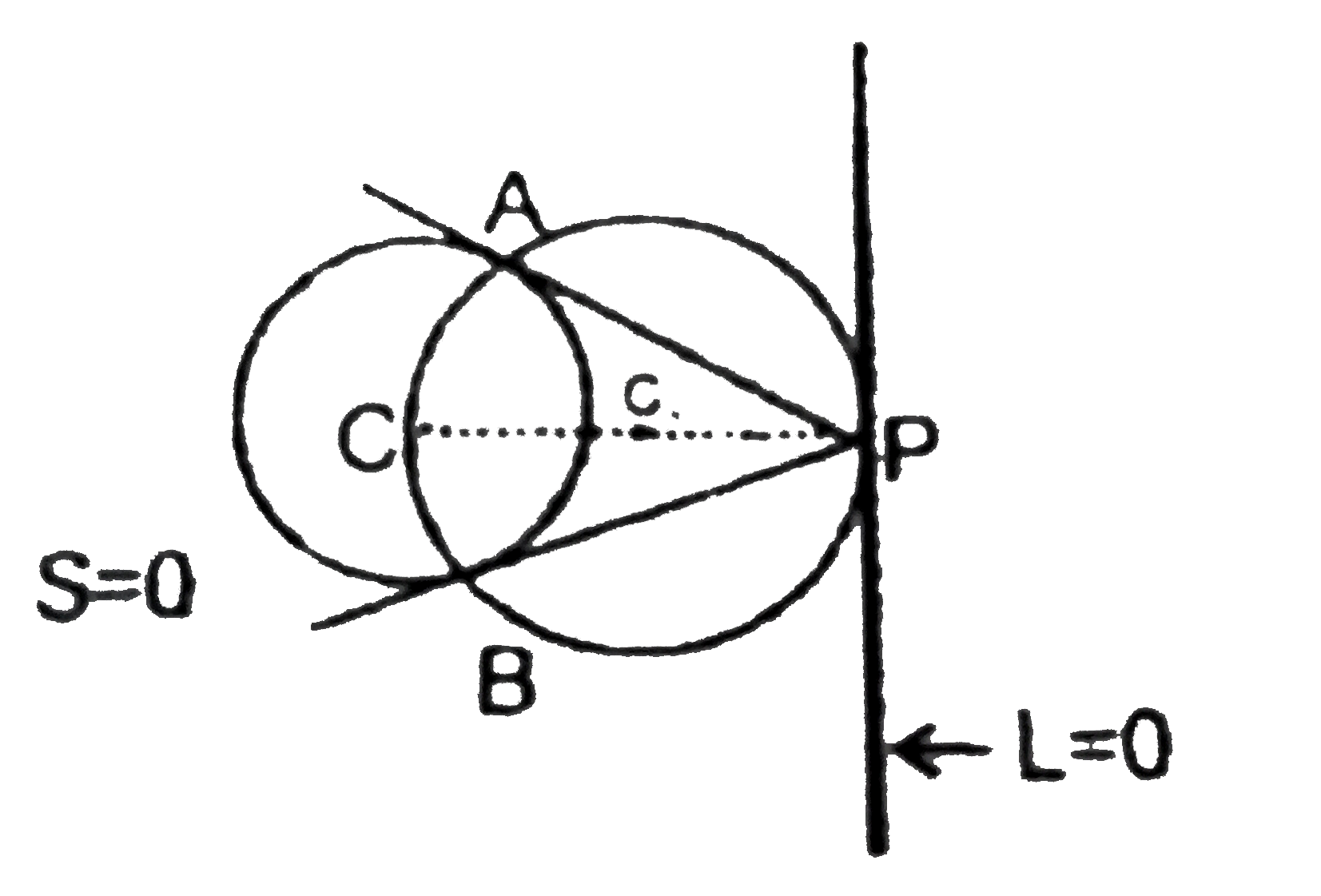 The circumcirle of `DeltaPAB` PASSES through C with PC as its diameter. Therefore centre of this circle `(C_(1))` will be MID pt of PC. Let `L=ax+by+c=0` `P(x_(1).y_(1)) & C(p,q)` `C_(1)(H,k)` `h=(x_(1)+p)/(2)` `k=(y_(1)+q)/(2)` `p(x_(1),y_(1))` passes through `L=0` `impliesax_(1)+by_(1)+c=0` or `a(2h-p)+b(2k-q)+c=0` or `2ah+2bk-ap-bq+c=0` Locus of `(h,k)` is `ax+by=(ap+bq+c)/(2)` `implies` A line parallel to `L=0` |
|