InterviewSolution
Saved Bookmarks
| 1. |
what are thesalientfeature of Crystal FieldTheory(CFT) ? |
|
Answer» Solution :Bethe and vanVleckdeveloped Crystal FieldTheory (CFT) TOEXPLAIN variousproperties of coordinationcompounds . Thesalientfeatureof CFT are as follows: (1) In a complex , the CENTRAL metal atom or ions is surrounded by various ligands whichareeithernegativelycharged ions `(F^(-),Cl^(-), CN^(-))` etc.ornetural molecules `(H_(2)O,NH_(3))` en etc.) and the mostelectronegativeatom in themor ionand thesurroundingligandsact as pointtowardscentralmetal ions . (2) The metalatom or ions and the surroundingligandsact as pointcharges involvingpurely electrosn attractionbetweenthem. (3) (i)Thecentralmetal ion has five ( n -1) d degenerateorbitalsnamely `d_(xy),d_(yz),d_((x^(2)-y^(2)) and d_(z^(2))` (II)Whenthe ligandsapproch themetalion, dueto repulsiveforces, the degeneracyof d-orbitalsis destroyedand they split into two groups of differentenergy `t_(2g)` and `e_(g)`orbitals. This effect is calledcrystal filed splittingwhichdependsuponthe geometryof thecomplex. (iii)The d-oribtalslying in thedirections of ligands are affected to agereater extentwhile thoselyingin betweenthe ligandsare affectedto a lessextent. (iv) Due torepulsion, the orbitalsalongthe axesof ligands acquirehigherenergywhilethoselying in betweentheligands acquirelessenergy . (v) Hencerepulsion by ligands GIVE tow sets of split up orbitalsofmetal ion withdifferentenergies. 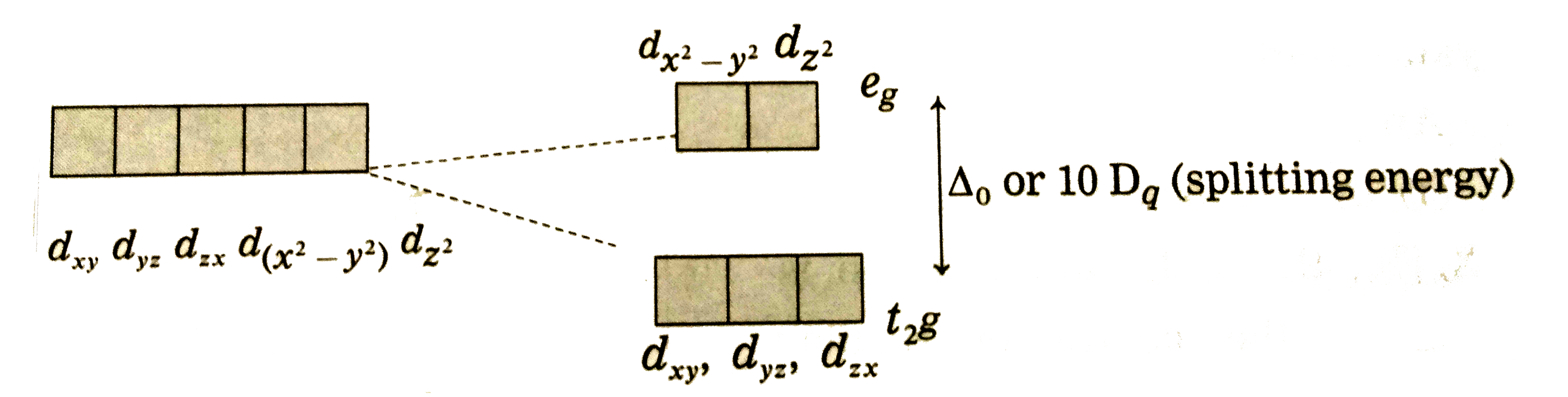 (vi)Theenergy differencebetweentwo sets of d-orbitalsaftersplittingby ligands is calledcrystal field splittingenergy(CFSE) andrespesented by `Delta_(0)`or by arbitrary term`10D_(q)`. Thevalue of `Delta` or `10Delta_(q)`dependsupon thegeometryof the complex. 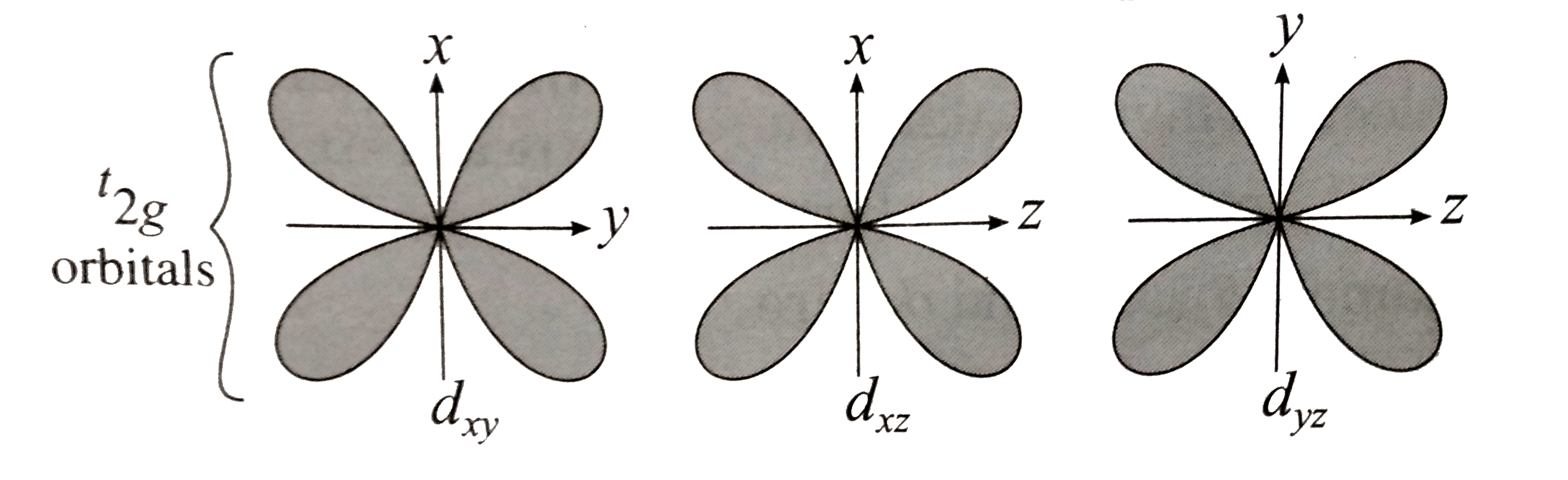  (4) Theelectrons of metalionoccupythe split d-orbitalsaccordingto Hund's ruleaufbauprincipleand thoseorbitalswithminimum repulsionand the firsthestawaysform theligands. (5) CFTdoes notaccountfor overlappingof orbitals of central metal ion and ligands , hencedoes notconsidercovalentnatureof thecomplex. (6) From thecrystal fieldstability ENERGY , the stability of thecomplexcan beknown. |
|