InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 5301. |
Evaluate the following limits : Lim_(xto 0) (sin (x +h)- sin x)/h |
|
Answer» |
|
| 5303. |
The sum of two + ve numbers is 100 . If the product of the square of one number and the cube of the other is maximum then the numbers are |
|
Answer» `60.40` |
|
| 5304. |
Which one of the following pair of straight lines are parallel? |
|
Answer» `x-2y-4=0,`2x-3y-4=0` |
|
| 5305. |
Draw the graph of the following quadratic functions. Q. y=x^(2)-5x+6""0lexle5. |
|
Answer» |
|
| 5306. |
Find the variance and standard deviation from the following data: |
Answer» Solution :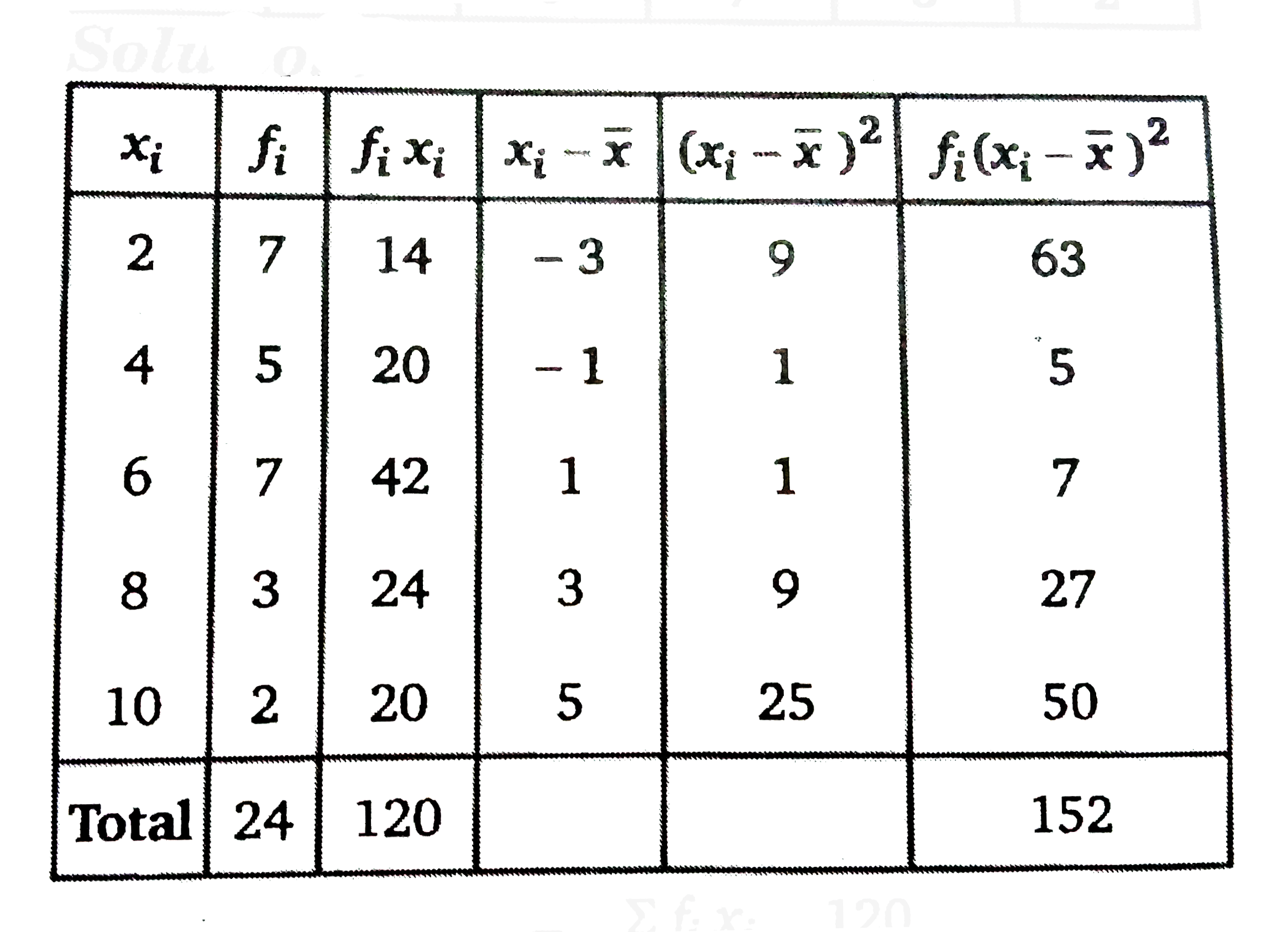 Arithmetic mean `BAR=(sumf_(i)x_(i))/(sumf_(i))=120/24=5` Variance `sigma^(2)=(sumf_(i)(x_(i)-barx)^(2))/(sumf_(i))=152/24=6.33` Standard DEVIATION `sigma=sqrt(6.33)=2.52` |
|
| 5307. |
A quadratic equation whose roots are tan22""1^@/2 and cot22""(1^@)/2 is |
|
Answer» `x^2 -2sqrt2x+1=0` |
|
| 5308. |
Find the sum of n terms of each of the following 1^(2) + ((1^(2) + 2^(2))/(2)) + ((1^(2) + 2^(2) + 3^(2))/(3))+ ….. |
|
Answer» |
|
| 5309. |
Three coins tossed. Describe. (i) Two events which are mutually exclusive. (ii) Three events which are mutully exclusive and exhaustive. (iii) Two events, which are not mutually exclusive. (iv) Two events which are mutually exclusive but not exhaustive. (v) Three event which are mutually exclusive but not exhaustive. |
|
Answer» |
|
| 5310. |
lim(x to 0)(sin|x|)/(x) is |
|
Answer» 1 |
|
| 5311. |
The points with P.V's bar(i)+2bar(j)+bar(k), 2bar(i)+3bar(j)+4bar(k) and 4bar(i)+5bar(j)+10bar(k) form |
|
Answer» An ACUTE ANGLED TRIANGLE |
|
| 5312. |
If OABCis a tetrahedronsuch that OA^(2)+BC^(2)=OB^(2)+CA^(2)=OC^(2)+AB^(2)= then |
|
Answer» `OA bot BC` |
|
| 5313. |
Let f:R rarr R be a continuous function such that f(x)-2 f(x/2) + f(x/4)=x^(2). Now answer the following The equation f(x)-x-f(0)=0 have exactly |
|
Answer» no SOLUTION |
|
| 5314. |
Show that the locus of the mid - point of the segment intercepted between the axes of the variable line x cos alpha + y sin alpha = pis 1/x^2+1/y^2=4/p^2 where p is a constant . |
|
Answer» |
|
| 5315. |
The pressure p and the voluem v of a gas are connected by the relation pv = 300. If the volume is increasing at the rate of 0.6 cubic cm minute then the rate of change in pressure of the gas when the volume is 30 cubic cm is |
|
Answer» 2 units/min |
|
| 5316. |
Solve : sec x cos 5x+1=0 , where 0ltxle(pi)/(2). |
|
Answer» |
|
| 5317. |
Theperiodof (cos(3 x+ 4) + tan (5x+7))/( cosec (3+4x) - sin(4-6x) is |
| Answer» ANSWER :3 | |
| 5318. |
A line segmentPQ has the length 63 and d.rs (3, -2, 6). If the line makes obtuse angle with X-axis, then components of vector bar(PQ) are |
|
Answer» `-27, -18, -54` |
|
| 5319. |
{:("Column-I", "Column-II"), ("A) "x in[pi, 2pi] rArr abs(tan^(-1)(tanx))" can be", "p) "abs(x-2pi)), ("B) "x in [pi, 2pi] rArr abs(cot^(-1)(cotx))" can be", "q) "abs(x-pi)), ("C) "x in [-pi, pi]rArr abs(sin^(-1)(sinx)), "r) "abs(x)), ("D) "x in [-pi, pi] rArr abs(cos^(-1)(cosx)), "s) "abs(x+pi)):} |
|
Answer» |
|
| 5320. |
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (-1, -1) are the vertices of a right angled triangle. |
|
Answer» |
|
| 5321. |
Match the following {:("Column - I ","Column - II "),("a) The number of solutions of " sum_(r = 1 )^(5) cos r x = 5" in the interval " [0, 2 pi] is ,"p) 0 "),("b) Number of solutions of the equations " y = (1)/(3) [ sin x + [ sin x [ sin x ]]]and [y + [y]]= 2 cos x " where " [*] " denotes greatest integer functionis ","q) 1 "),("c) The number of solutions of " log |sin x| = - x^(2) + 2x " when " x in [(-pi)/(2), (3 pi)/(2)] is ,"r) 2 "),("d) The total number of solutions of the equation " 3 x + 2 tan x = (5 pi)/( 2) " in " x in [ 0, 2 pi ] " is equal to " ,"s) "):} |
|
Answer» |
|
| 5322. |
The P.V.'s of A, B are bar(a), bar(b) respectively. The P.V. of 'C' is bar(a)/2+bar(b)/3 then 'C' lies |
|
Answer» OUTSIDE `DELTAOAB` but INSIDE `angleOAB` |
|
| 5323. |
The transformedequation of (x^(2))/(a^(2))-(y^(2))/(b^(2))=1 when the axes are rotated through an angle 90^(0) is |
|
Answer» `(X^(2))/(a^(2))-(Y^(2))/(B^(2))=1` |
|
| 5324. |
If the equation of line is x = ay + b : z = cy +d. Then its symmetric form is |
|
Answer» `(X-a)/(B) = y/1 = (Z-C)/(d)` |
|
| 5325. |
Find the number of terms in the expansion of the following : (2a+5b)^(9)-(2a-5b)^(9) |
|
Answer» |
|
| 5326. |
4 cos36^@+cot7(1^@)/2= |
|
Answer» `1+sqrt2+sqrt3+sqrt4+sqrt5+sqrt6` |
|
| 5327. |
Find the mean deviation about the mean for the following data : 12, 3, 18, 17, 4, 9, 17, 19, 20, 15, 8, 17, 2, 3, 16, 11, 3, 1, 0, 5 |
|
Answer» |
|
| 5328. |
.............is the necessary condition if solution region of ax + by + c gt 0 contains origin. (0,0) . |
|
Answer» |
|
| 5329. |
If : 4(sin 3 theta * cos^(3) theta * 3 theta * sin^(3) theta)=m * sin (ntheta), "then" : (m,n)-= |
|
Answer» (1,2) |
|
| 5330. |
Fill in the blank by choosing the correct answer from the bracket. If z is any complex number, zoverlinez=…. (absz^2, absz, 0, 1) |
|
Answer» |
|
| 5331. |
If the two pair of lines 2x^(2)+6xy+y^(2)=0 and 4x^(2)+18xy+by^(2)=0 are equally inclined to each other then b= |
| Answer» ANSWER :A | |
| 5332. |
If (3pi)/4ltA/2lt(5pi)/4 then -sqrt(1+sinA)+sqrt(1-sinA)= |
|
Answer» `2"COS"A/2` |
|
| 5333. |
The equation of the normal to the curve x^(2)=4y at (1,2) is |
|
Answer» X + y = 3 |
|
| 5335. |
Write the negation of the following simple statements. 2 is not a prime number. |
|
Answer» |
|
| 5336. |
If the area of a cyclic quadrilateralABCD is (3 sqrt(3))/(4) . The radius of its circumcircle is 1. If AB=1, BD= sqrt(3) then BC.DC= |
|
Answer» 1 |
|
| 5337. |
In a certain college 4% of the boys and 1% or the girls are taller than 1.8 meter. Further 60% of the students are girls. If a student is selected at random and is taller than 1.8 meters, than the probability that the student is a girl is : |
|
Answer» `(2)/(11)` |
|
| 5338. |
If f={(1,2),(2,3),(3,5),(5,8)} and g={(2,1),(3,2),(5,3),(8,5)} then f@g= |
|
Answer» `{(1,2),(2,3),(3,5),(5,8),(2,1),(3,2),(5,3),(8,5)}` |
|
| 5339. |
Rewrite each of the following statements in the form of conditional statements: The square of a prime number is not prime. |
|
Answer» |
|
| 5340. |
Find the sum to n terms of the A.P., whose k^("th")term is 5k + 1. |
|
Answer» |
|
| 5341. |
Fill in the blanks to make each of the following a true statement : A cap (A cup B)="…………" |
|
Answer» |
|
| 5342. |
A persons has got 12 friends of whom 8 are relatives. In how many ways can he invite 7 guests such that 5 of them may be relatives ? |
|
Answer» |
|
| 5345. |
Find the centre of the ellipse, (x^(2)-ax)/a^(2)+(y^(2)-by)/b^(2)=0. |
|
Answer» |
|
| 5346. |
((sinA)/(1-cosA))-((1-cosA)/(sinA))= |
|
Answer» `2 TAN A` |
|
| 5347. |
If A and B are two symmetric matrices then AB + BA is |
|
Answer» symmetric |
|
| 5348. |
Find the point to which the origin has to shifted to eliminate x and y terms in the equation 3 (x - 2)^(2) + 5 (y + 3)^(2) = 6 |
|
Answer» |
|
| 5349. |
If y = f((3x+4)/(5x+6)) and f^(1)(x) = tanx^2then (dy)/(dx) is equal to |
|
Answer» `-2TAN((3x+4)/(5x+6))^2XX1/((5x+6)^2)` |
|
| 5350. |
Which of the following sentences are statements? Give reasons for your answer There are 35 days in a month. |
|
Answer» |
|