InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 551. |
The profit function P(x) of a company selling x items per day is given by P(x) = (150-x)x - 1000. Find the number of items that the company should manufacture to get maximum profit. Also find the maximum profit. |
|
Answer» |
|
| 552. |
If in DeltaABC,A=(pi)/(7),B=(2pi)/(7),C=(4pi)/(7) y then a^(2)+b^(2)+c^(2) must be |
|
Answer» `R^(2)` |
|
| 553. |
Reduce the following equations into slope intercept form and find their slopes and the y- intercepts. (i) x+7y=0 |
|
Answer» |
|
| 554. |
Reduce the following equations into slope intercept form and find their slopes and the y- intercepts. (ii) 6x+3y-5=0 |
|
Answer» |
|
| 555. |
Reduce the following equations into slope intercept form and find their slopes and the y- intercepts. (iii) y=0 |
|
Answer» |
|
| 556. |
AA t in R suppose [t] has value t of all integer value of less than t then, lim_(xto0+)x([(1)/(x)]+[(2)/(x)]+........+[(15)/(x)]) |
|
Answer» EQUAL to 0 |
|
| 557. |
Which of the following can not be valid assignment of probabilities for outcomes of sample Space S = {omega_(1), omega_(2), omega_(3), omega_(4), omega_(5), omega_(6), omega_(7)} Assignment omega_(1)" "omega_(2)" "omega_(3)" "omega_(4)" "omega_(5)" "omega_(6) (a) 0.1 0.01 0.05 0.03 0.01 0.2 0.6 (b) 1/7 1/7 1/7 1/7 1/7 1/7 1/7 (c) 0.1 0.2 0.3 0.4 0.5 - 0.6 - 0.7 (d) -0.1 0.2 0.3 0.4 -0.2 0.1 0.3 (e) 1/14 2/14 3/14 4/14 5/14 6/1415/14 |
|
Answer» |
|
| 558. |
The set of points of discontinuily of thef(x) = (1)/(x^(2) + 4x + 5) |
| Answer» ANSWER :A | |
| 559. |
Find the point to whichthe origin is to be shifted so thatthe point (3, 0) may change to (2,-3) |
|
Answer» |
|
| 560. |
Write the values of x and y if (3-4i) (x + yi) =1 + i(0) |
|
Answer» |
|
| 562. |
Find deltay and dy for the following functions y=x^(2)+3x+6,x=10,deltax=0.01 |
|
Answer» |
|
| 563. |
A particle moves on a line according to the law s = at^(2) + bt + c. If the displacement after one second is 16 cm, the velocity after 2 second is 24 cm/sec and the acceleration is 8cm//sec^(2). Then (a,b,c) |
|
Answer» (4,8,6) |
|
| 564. |
{:("Column -I","Column - II"),("A) If maximum and minimum values of" ( 7+6 tan theta - tan^(2) theta)/(( 1 + tan^(2) theta) ) "for all real values of" theta ne (2n+1) (pi)/(2) "are" lambda " and u respectively then","p)" lambda+ mu =2),("B) If maximum and minimum values of" 5 cos theta + 3 cos ( theta + (pi)/(3) +3)"for all real values of" theta "are" lambda "and u respectively then" ,"q)"lambda- mu =6),("C) If maximum and minimum values of" 1+ sin((pi)/(4) + theta) + 2cos ((pi)/(4) - theta) "for all real values of" theta "are" lambda and mu "respectively then","s)" lambda- mu = 10),(,"t)" lambda- mu =14):} |
|
Answer» |
|
| 565. |
Let a,b,c,d,e,f,g,h be distinct elements in the set {-7,-5,-3,-2,2,4,6,13} . The minimum value of (a+b+c+d)^(2)+(e+f+g+h)^(2) is |
|
Answer» 30 |
|
| 566. |
Find the transformed equation of 4xy-3x^(2) = a^(2) when the axes are rotated through an angle Tan^(-1)2. |
|
Answer» |
|
| 567. |
If n is an odd positive integer, prove that the coefficients of the middle terms in the expansion of (x+y)^(n) are equal. |
|
Answer» |
|
| 570. |
Show that (a^(2))/( 4) sin 2c +(c^(2))/( 4) sin 2A = Delta |
|
Answer» |
|
| 571. |
State whether word or is used in following statement is Exclusive or Inclusive. Proof at identity is Pancard or Bank passbook. |
|
Answer» |
|
| 573. |
If oneof lines in ax^(2)+2hxy+by^(2)=0 bisects the angle between the coordinates axes then (a+b)^(2)= |
|
Answer» `2H^(2)` |
|
| 574. |
Letf(x)=(2x(sin x + tanx))/(2[(x+21pi)/(pi)]-41),x != n pi,then f is ( where [.] represents greatest integer function) |
|
Answer» an ODD function |
|
| 576. |
From4 red balls, 2 white balls and 4 blackhalls , four halls are selected . The probabilityof getting 2 red balls is |
|
Answer» `(7)/(21)` |
|
| 577. |
I: The system of equations x+y+z=6,x-y+z=2, 2x-y+3z=9 has unique solution. II: The system of equations x+y+z=3, 2x+2y-z=3,x+y-z=1 has infinitely many solutions |
|
Answer» only I is TRUE |
|
| 580. |
Evaluate the following limits. Lt_(xto pi)(x-22/7) |
|
Answer» |
|
| 581. |
If U = {1, 2, 3, 4, 5, 6, 7, 8, 9 }, A = {2, 4, 6, 8} and B = { 2, 3, 5, 7}. Verify that (A ∪ B)′ = A′ ∩ B′ |
|
Answer» |
|
| 583. |
If 2S=a+b+c, prove that |{:(a^(2),(S-a)^(2),(S-a)^(2)),((S-b)^(2),b^(2),(S-b)^(2)),((S-c)^(2),(S-c)^(2),c^(2)):}|=2S^(3)(S-a)(S-b)(S-c). |
|
Answer» |
|
| 584. |
|{:(a-b-c,2b,2c),(2a,b-c-a,2c),(2a,2b,c-a-b):}|= |
|
Answer» `(a+b+c)^(3)` |
|
| 585. |
If tantheta+tan2theta+sqrt(3)tanthetatan2theta=sqrt(3), then theta=(npi)/(3)+(pi)/(9). |
|
Answer» |
|
| 586. |
If y is an implicit funtiion of x given by the relation, find (dy)/(dx). x ^(2) + y ^(2) + 2x + 3y -4 =0. |
|
Answer» |
|
| 587. |
Find the co-ordinates of the point of intersection of the straight lines 2x-3y-7=0 , 3x-4y-13=0 |
|
Answer» |
|
| 588. |
Find the term independent of x in the expansion of (root(3)(x)+1/(2root(3)(x)))^18,x > 0. |
|
Answer» |
|
| 589. |
The sum and product of three consecutive terms of an A.P. are 24 and 312 respectively. Find these terms. |
|
Answer» |
|
| 590. |
Find the mean deviation by short cut method. |
Answer» SOLUTION :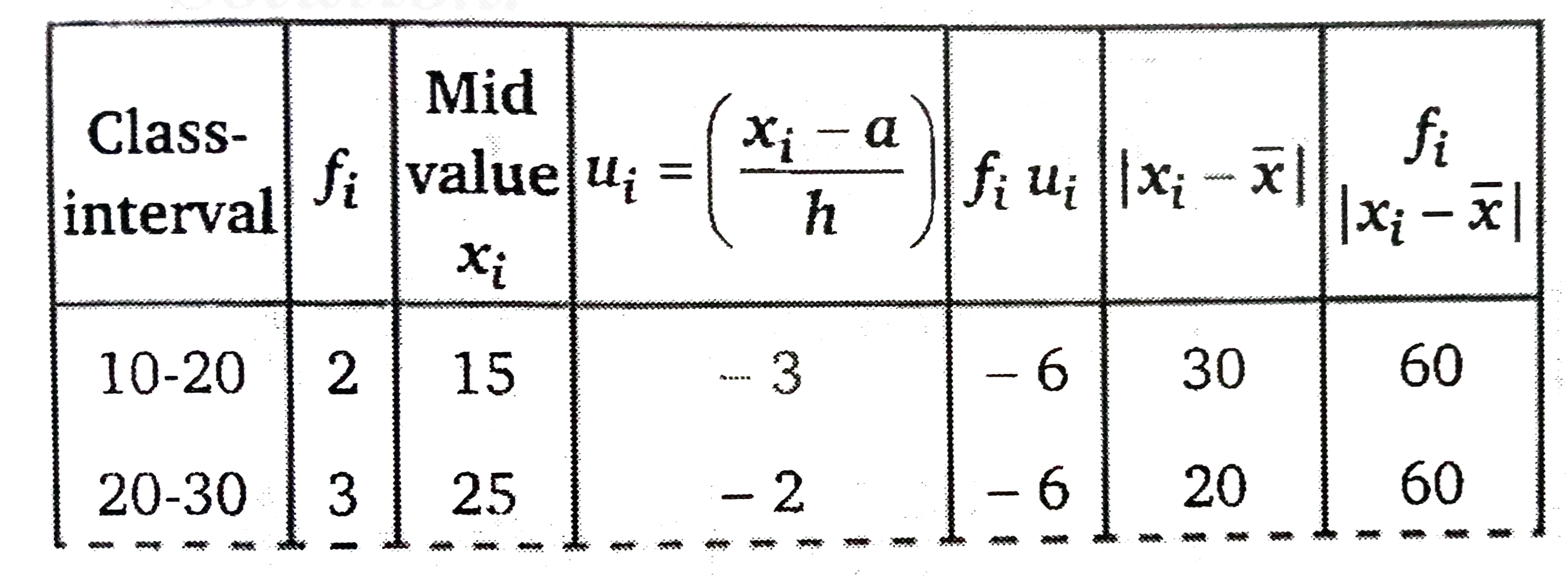  Let `a=45, h=10` Arithmetic MEAN `BARX=a+(sumf_(i)(u_(i)))/(sumf_(i))xxh` `=45+0/40xx10=45` Mean deviation `=(sumf_(i)|x_(i)-barx|)/(sumf_(i))` `=400/40=10` |
|
| 591. |
Form the bicoditional statement phArrq. Where p: Natural number n is odd. q: Natural number n is not divisible by 2. |
|
Answer» |
|
| 592. |
If A(1, -1, -3), B(2, 1, -2), C(-5, 2, -6) are the vertices of a DeltaABC, then the length of internal bisector of angle A is |
|
Answer» `3/4sqrt(10)` |
|
| 593. |
(sqrt(2)-sin alpha - cos alpha)/(sin alpha - cos alpha) is equal to |
|
Answer» `SEC((alpha)/(2)-(pi)/(8))` |
|
| 595. |
Statement-1 : Condition of Lagrange's mean value theorem fail in f(x) = | x-1 | (x-1). Statement-2 : |x-1| is not differentiableat x=1 . |
|
Answer» If both the statement are TRUE and STATEMENT 2 is the correct EXPLANATION of STATMEMENT -1 |
|
| 596. |
Equilateral triangle DEF is inscribed in equilateral triangle ABC as shown with DE bot^("lar")B Cthen ratio of Area of triangle DEF to the Area of Delta^("le") ABC is then |
| Answer» ANSWER :A | |
| 597. |
Separate the intervals of monotonicity of the following functions : f(x) = -sin^(3)x + 3 sin^(2)x + 5, x in [-pi//2, pi//2] |
|
Answer» |
|
| 598. |
If the distance between the pair of parallel lines x^(2)+2xy+y^(2)-8ax-8ay-9a^(2)=0 is 25sqrt2, then |a|= |
|
Answer» 1 |
|
| 599. |
If (5,-2),(-2,1) and (9,6) are collinear find alpha. |
|
Answer» |
|
| 600. |
Express sin "" (5pi)/(2) in terms ofcos 5pi , |
|
Answer» |
|