InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 10901. |
R = {(a, b)": a in N, b in N, a+ 3b = 12}. Express R as roster method. Find the domain and range of R. |
|
Answer» |
|
| 10902. |
The solution of (81)^(sin^(2)x) +(81)^(cos^(2)x)=30 in [0, pi//2] is |
|
Answer» `pi//4 or pi//2` |
|
| 10903. |
(ii) Find the value of sin^(2). (pi)/(4) + sin^(2). (3pi)/(4) + sin^(2). (5pi)/(4)+ sin^(2). (7pi)/(4). |
|
Answer» |
|
| 10904. |
If the equation lambda x^(2)-5xy+6y^(2)+x-3y=0 represents a pair of straight lines then their point of intersection is |
| Answer» ANSWER :A | |
| 10905. |
Figure |
|
Answer» |
|
| 10906. |
A set of vectors bar(a)_(1), bar(a)_(2), ………, bar(a)_(n) is said to linearly independent if every relation of the form l_(1)bar(a)_(1)+l_(2)bar(a)_(2)+……….+l_(n)bar(a)_(n)=bar(0) implies |
|
Answer» `l_(1)=l_(2)=…………..=l_(N)=1` |
|
| 10907. |
Explain why 3x^(2)+kx-1 is never always positive for any value of k. |
|
Answer» |
|
| 10908. |
A sample of 35 observations has mean 80 men and standard deviation 4. A second sample of 65 observations has mean 70 and standard deviation =3. Find the combined mean and standard deviation. |
|
Answer» |
|
| 10909. |
If x, 2y and 3z are in AP where the distinct numbers x,y and z are in GP, then the common ratio of the GP is |
| Answer» ANSWER :B | |
| 10910. |
solve the equation: 2^(2x) -2^(x+2)-4xx2^(3)=0. |
|
Answer» |
|
| 10911. |
Assertion : Parade of soldiers can be two dimension at or one dimensional Reason : If the soldiers followed a straight line then it is one dimensional motion if they take a curved path after some time, that is an example for two dimensional motion. |
|
Answer» ASSERTION and Reason are CORRECT and Reason is correct explanation of Assertion |
|
| 10912. |
If the sum of any number of consecutive terms of a sequence is always nine times the squared number of these terms then the sequence is a/an |
|
Answer» A.P. |
|
| 10913. |
cos(47^@) cos (13^@) - sin (47^@) sin(13^@)= ......... |
|
Answer» |
|
| 10915. |
If r_1 , r_2 , r_3are the radii of the escribed circles of a Delta ABCand if r is the in radius then r_1r_2r_3-r( r_1r_2+r_2r_3+r_3r_1) |
| Answer» ANSWER :A | |
| 10916. |
Find the equation of a line perpendicular to the line x - 2y + 3 = 0and passing through thepoint (1, -2). |
|
Answer» |
|
| 10917. |
State which of the following sets are finite or infinite : {x : x in N" and "x^(2)= 4} |
|
Answer» |
|
| 10918. |
The range of f(x)=cot^(-1)(2x-x^(2)) is |
|
Answer» `[(PI)/4,pi]` |
|
| 10919. |
2x + y ge 2,x - y le 1,x + 2y le 8,x ge 0, y ge 0. |
Answer» 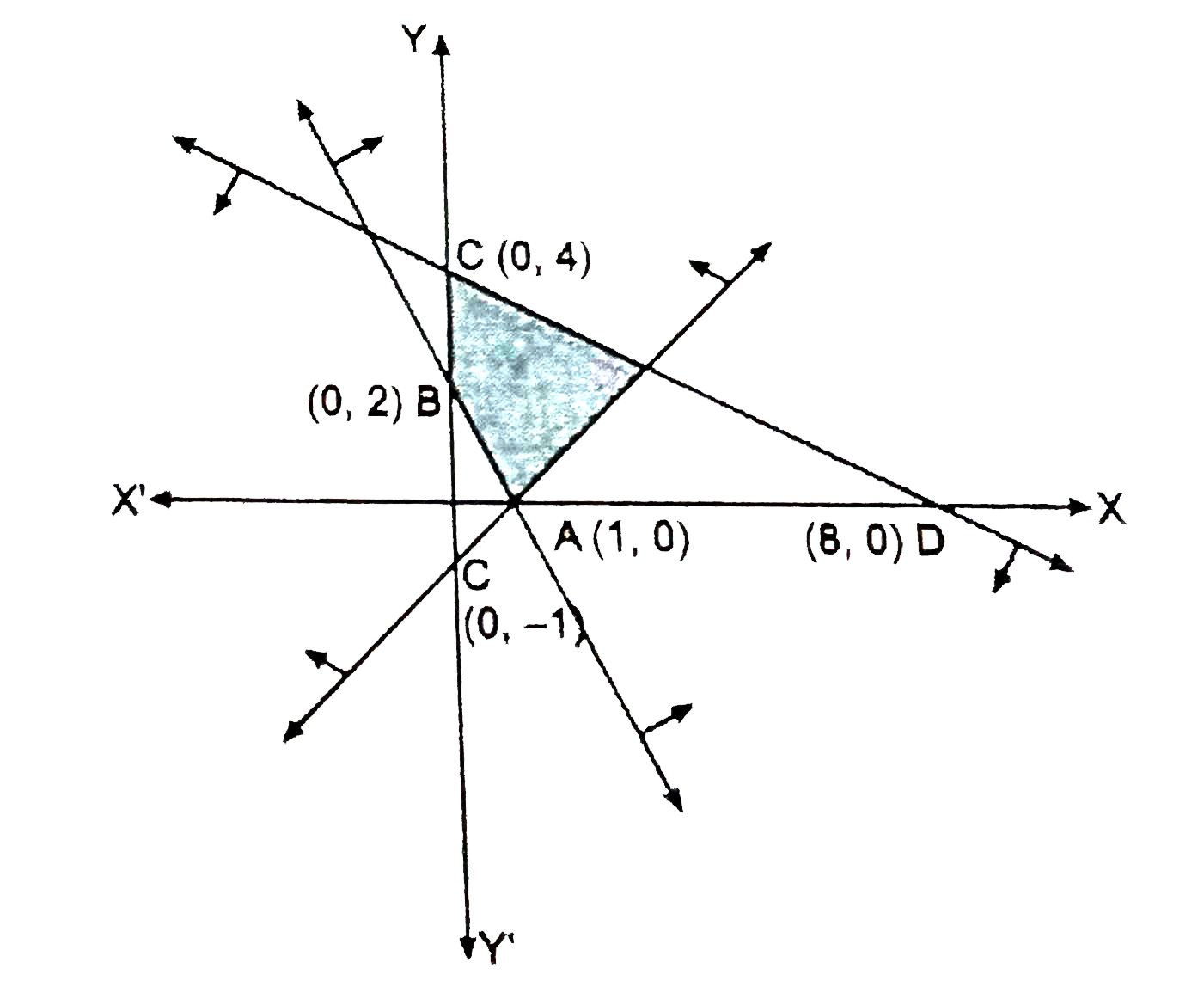
|
|
| 10920. |
f: N rarr N is defined asf(n) = {{:(2","n=3",",k in Z),(10-n","n=3k+1",",k in Z),(0","n=3k+2",",k in Z):}then {n in N : f(n) gt 2}= |
|
Answer» `{3,6,4}` |
|
| 10921. |
If a,b,c are three terms in A.P and a^(2), b^(2), c^(2) are in G.P. and a + b+ c = (3)/(2) then find a. (where a lt b lt c) |
|
Answer» |
|
| 10922. |
Find the condition that the point (h, k) may lie on the curve x^(2)+y^(2)+5x+11y-2=0. |
|
Answer» |
|
| 10923. |
Assertion (A): cos^(3)x+cos^(3)(120^(@)+x)+cos^(3)(120^(@)-x)=3/4cos3x Reason (R ): costheta+cos(120^(@)+theta)+cos(120^(@)-theta)=0 and costheta.cos(120^(@)+theta).cos(120^(@)-theta)=1//4 cos 3 theta |
|
Answer» A is true, R is true and R is CORRECT explanation of A |
|
| 10924. |
Let A ={a,b,c}, B={b,c, d,e} and C={c,d,e,f}be subsets of U={a,b,c,d,e,f}. Then,verify that:(i) (A')'=A(ii)(A cup B)'=(A' cap B')(iii) (A cap B)'=(A'cup B') |
| Answer» | |
| 10925. |
If vecA,vecB,vecC are three non-coplanar vectors such that abs(vecA)=4,abs(vecB)=5,abs(vecC)=6 then [vecA-vecB,vecB-vecC,vecC-vecA]= |
|
Answer» 120 |
|
| 10926. |
The solutions of the system of equations x+y=2pi//3 and cos x + cos y = 3//2 where x and y are real, are |
|
Answer» `X = PI, y = - pi//3` |
|
| 10928. |
Thevalue of sin theta sin((pi)/(3) - theta) sin ((pi)/(3) + theta)liesin (p,q)then p=andq= |
|
Answer» `-(1)/(4),(3)/(4)` |
|
| 10929. |
If the coefficient of second , thirdand fourth terns in the expansion of (1+x)^(2n) are in AP, then show that 2n^(2)-9n + 7 = 0 |
|
Answer» |
|
| 10931. |
A function f is defined byf(x) = (2x-5) write the value of (i) f(7) (ii) f(-3) ? |
|
Answer» |
|
| 10932. |
Evaluate the following limits in lim_(xrarr0)(sinax)/(sinbx),a,b ne0 |
|
Answer» |
|
| 10933. |
For the equation Cos^(-1)x+Cos^(-1)2x+pi=0 the number of real solution is |
|
Answer» 0 |
|
| 10934. |
The sum of series sec^(-1)sqrt(2)+"sec"^(-1)(sqrt(10))/3+"sec"^(-1)(sqrt(50))/7+…………..+sec^(-1)sqrt(((n^(2)+1)(n^(2)-2n+2))/((n^(2)-n+1)^(2))) is |
|
Answer» `TAN^(-1)1` |
|
| 10936. |
Find the number of different words that can be formed from the letters of the word TRIANGlE, so that no vowels are together. |
|
Answer» |
|
| 10937. |
Let P_(r)(x_(r),y_(r),z_(r)), r=1,2,3 " be three points where" x_(1),x_(2),x_(3),y_(1),y_(2),y_(3), z_(1),z_(2),z_(3) are each in G.P. with the same common rato then P_(1),P_(2),P_(3) are |
|
Answer» coplanar |
|
| 10938. |
Marks obtained by 10 students in exam of 70 Marks are as follows. 53,46,48,50,53,53,58,60,57 and 52 Then range of data is ..... |
|
Answer» |
|
| 10939. |
Find the sum to indicated number of terms in each of the geometric progressions in x^3,x^5,x^(7), .........n terms (if x ne pm 1) |
|
Answer» |
|
| 10940. |
Find the domain and range of the following real functions: (i)f(x)=sqrt(9-x^(2)) |
|
Answer» (II) Domain of function `={X: -3 le x le 3}` Range of function `={x : 0 le x le 3}` |
|
| 10941. |
The sides of a right angled triangle are in A.P then they are in the ratio |
|
Answer» `1:2: SQRT(2)` |
|
| 10943. |
A rayof light comes along the line L =0 and sirikes the plane mirror kept along the plane P = 0 at B. A (2,1,6) is a point on the line L =0 whose image about P =0 is A'. It is given thatL = 0 is(x-2)/(3)= (y-1)/(4) = (z-6)/(5) and P = 0 is x + y - 2z = 3 The coordinates of B are |
|
Answer» `(5,10,6)` |
|
| 10944. |
A rayof light comes along the line L =0 and sirikes the plane mirror kept along the plane P = 0 at B. A (2,1,6) is a point on the line L =0 whose image about P =0 is A'. It is given thatL = 0 is(x-2)/(3)= (y-1)/(4) = (z-6)/(5) and P = 0 is x + y - 2z = 3 If L _(1) =0 is the reflected fay, then its equation is |
|
Answer» `(x+10)/(4) = (y-5)/(4) = (z+2)/(3)` |
|
| 10945. |
A rayof light comes along the line L =0 and sirikes the plane mirror kept along the plane P = 0 at B. A (2,1,6) is a point on the line L =0 whose image about P =0 is A'. It is given thatL = 0 is(x-2)/(3)= (y-1)/(4) = (z-6)/(5) and P = 0 is x + y - 2z = 3 The coordinates of A' are |
|
Answer» `(6,5,2)` |
|
| 10946. |
A_(1), A_(2), A_(3), ……,A_(n) are the vertices of a regular plane polygon of n slides and O is the centre then show that underset(i=1)overset(n-1)Sigma bar(OA_(i)) xx bar(OA)_(i+1) = (1-n) (bar(OA)_(2) xx bar(OA)_(1)) |
|
Answer» |
|
| 10947. |
For the data given below, compute the index numbers for various years by taking 1997 as the base year: |
|
Answer» |
|
| 10948. |
A= {1, 2, 3, 4}, B= {-1, 1, 0, -2, 2}, C= {1, 3, 4} are subset of which set? |
|
Answer» `(1, 4)` |
|
| 10949. |
Lines L_(1):y-x=0 and L_(2):2x+y=0 intersect the line L_(3) : y+2=0at P and Qrespectively. The bisector of the acute angle between L_(1)and L_(2)intersects L_(3)at R. Statement-I: The ratio PR: RQ equals 2sqrt(2):sqrt(5) because. Statement II: In any triangle bisector of an angle divides the triangle into two similar triangles. |
|
Answer» STATEMENT 1 is correct and statement 2 is correct EXPLANATION of statement 1 |
|
| 10950. |
The sides of a Delta^("le") ABC " are " a = 4, b = 5, c = 6 The length of the external angular bisector of angle Cis |
|
Answer» `10 SQRT5` |
|