InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 4552. |
If A, B are acute positive angles satisfying the equations 3sin^(2)A+2sin^(2)B=1 and 3sin2A-2sin2B=0, then find A+2B. |
| Answer» Answer :`(pi)/(4)` | |
| 4553. |
If (1,2,3 ), (2,3,1 ) are two vertices of an equilateral triangle then its third vertex is |
|
Answer» (3,1,2) |
|
| 4555. |
A metallic scale, due to heat is showing 0.99 mts as 1 meter. In this state, the radius of the base and height of a cone are measured to be 1 mts each. Find the actual volume of the cone approximately. |
|
Answer» |
|
| 4556. |
Evaluate the following limits : Lim_(xto0) (sqrt((1+x+x^(2)))-1)/x |
|
Answer» |
|
| 4557. |
4x + 3y le 60, y ge 2x, x ge 3, x, y ge 0 |
|
Answer» Corresponding equation : `4x + 3y = 60` This line passes through the points A (15, 0) and B (0, 20). Join AB. At point (0, 0) from the inequation, `0le60` (TRUE) The solution of this inequation is that region of XY-plane DIVIDED by line AB in which (0, 0) lies. Seond inequation : `yge2x` Corresponding equation: `y = 2X` This line passes through the points O(0, 0) and C(5, 10) Join OC. At point (5, 0), from the inequation, `0 ge 10` (False) The solution of this inequation is that region of XY-plane divided byline OC in which (5, 0) does not lie. The solution of `xge 3 is x = 3` and its right side. The solution of `y ge 0 is y = 0 ` and its above. The common solution of given inequation is shown by the shaded region. 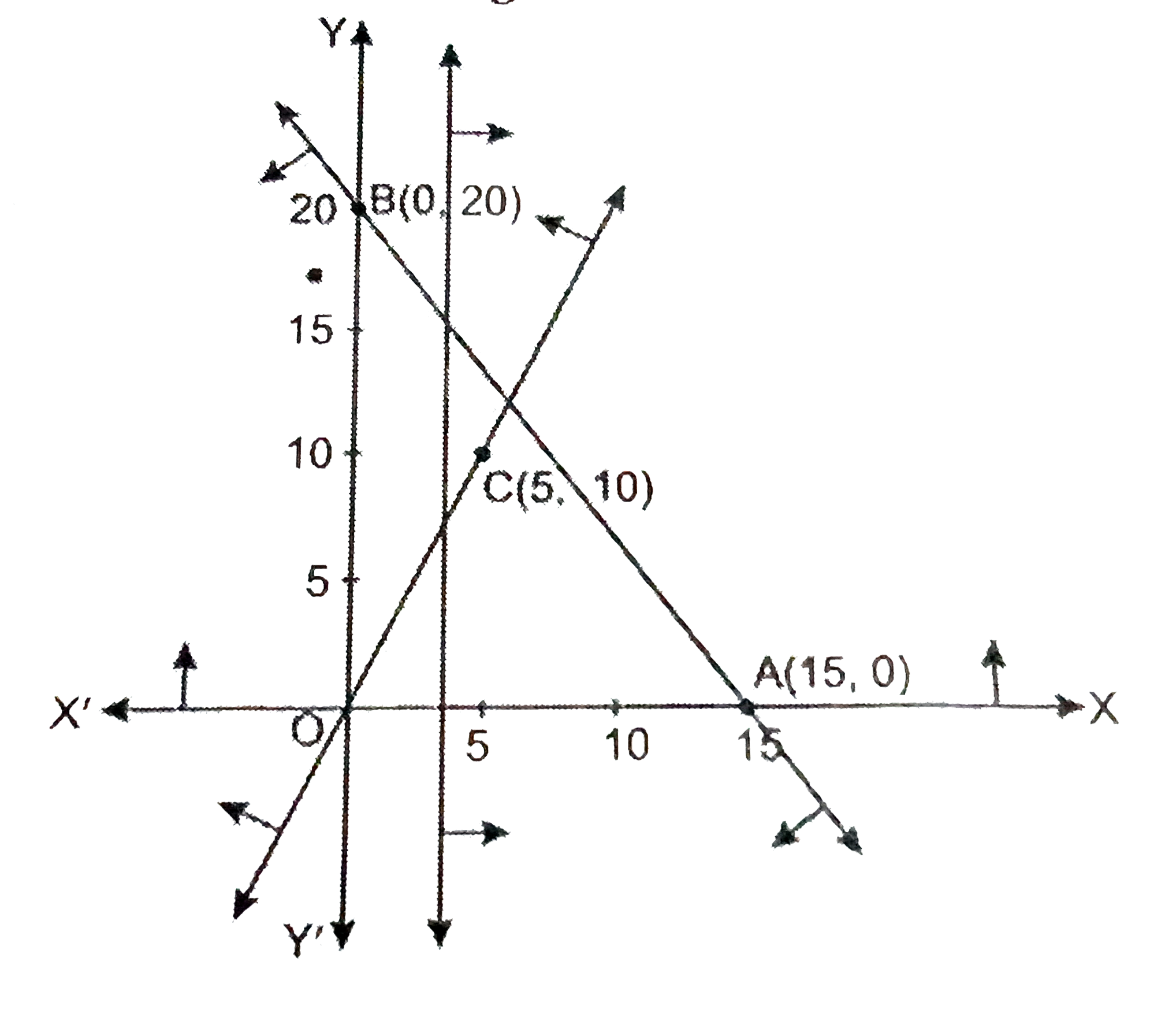
|
|
| 4558. |
Total numbers of 4 digits numbers using digits 5,2,3,7 and 8 are 620. |
|
Answer» |
|
| 4559. |
If (a+b+c) (b+c-a) = 3bc then find angle A . |
|
Answer» `60 ^(@)` 0 |
|
| 4560. |
Let L be the line 2x + y - 2 = 0 . The axes rotated by 45^(0) in clockwise direction thenthe intercepts made by the line L on the new axes are respectively . |
|
Answer» `1, SQRT(2)` |
|
| 4561. |
Find the equation of set of points P such that PA^(2)+PB^(2)=2k^(2), where A and B are the points (3, 4, 5) and (-1,3,-7), respectively. |
|
Answer» |
|
| 4562. |
Find the nth term and deduce the sum of n terms of the series 4+11+22+37+56+…………. |
|
Answer» |
|
| 4563. |
The odds in favour for three horses participating in a house-race are 1:3,2:5 and 3:7. Find the probability that any one can win the race. |
|
Answer» |
|
| 4565. |
n^( th) term of the series 4+14+ 30 + 52+ ….. |
|
Answer» `5n-1` |
|
| 4566. |
If (1+X+x^2)^n = Sigma_(r=0)^(2n)a_(r) x^r then prove that(a) a_(r)=a_(2n-r)(b ) Sigma_(r=0)^(n-1)a_(r)=1/2 (3^n-a_n) |
|
Answer» Solution :We have ` (1+X+x^2)^n = UNDERSET(r=0)OVERSET(2n)Sigma a_(r) x^r` Replace x by1/x `therefore (1 +1/x+1/(x^2))^n = underset(r=0)overset(2n) Sigma a_(r)((1)/(x))^r` `rArr(x^2+x+1)^n = underset( r=0)overset(2n)Sigma a_rx^(2n-r)` `underset(r=0)overset(2n ) a_(r)x^r =underset(r=0)overset(2n ) a_(r)x^r "" {"Using (A) "}` Equating the cofficient of `x^(2n-r)` on the both sides ,we get `a_(2n-r)= a_(r) " for " 0 LE r le 2n` Hence`a_(r)=a_(2n-r)` (b) Putting x=1 in given series , then `a_(0)+a_1 +a_2+......+a_(2n)=(1+1+1)^n` `a_(0)+a_(1)+a_(2)+...... +a_(2n)=3^n` But`a^r= a_(2n-r) for 0le r le4 2 n ` `therefore ` Series (1) reduces to `2(a_(0)+a_1+a_2+.......+a_(n-1)) + a_n =3^n` `thereforea_0+a_1+a_2+........+a_(n-1)= 1/2 (3^n-a_n)` |
|
| 4567. |
Solve the inequalityand represent the solution graphically on the number line ? |
|
Answer» |
|
| 4568. |
Draw the graphs of the following : y = |x| + |x -1| in [ -2,3] |
|
Answer» |
|
| 4569. |
Illustrate in the complex plane the following set of points and explain your answer |z-4| lt 1 |
|
Answer» |
|
| 4571. |
If 0 lt x lt pi, andcos x+ sin x =1//2, thentan x= |
|
Answer» `((4-sqrt(7)))/(3)` |
|
| 4572. |
Let f be function f(x)=cosx-(1-(x^(2))/(2)) . Then |
|
Answer» f(X) is an INCREASING functions in `(0,OO)` |
|
| 4573. |
LetA = { 1, 2, { 3, 4 }, 5 }. Which of the following statements are incorrect and why? {1, 2, 5} ⊂A |
|
Answer» |
|
| 4575. |
Find the derivatives of the function cos ^(-1) (( b + a cos x )/( a + b cos x )), (a gt 0, b gt 0) |
|
Answer» |
|
| 4576. |
The value that shouldbe assigned to f (0)so that the functionf(x) =(x + 1)^(cotx)is continuous |
| Answer» ANSWER :A | |
| 4577. |
Evaluate : lim_(xto 0) (10^(x) - 2^(x) -5^(x)+1)/(sin^(2)x) |
|
Answer» |
|
| 4578. |
Find the derivative of the following functions:3 cot x +5 cosec x |
|
Answer» |
|
| 4579. |
At a given instant, the sides OA and OB of a right angled triangled AOB are 8 cm and 6 cms respectively If OA increases at the rate of 2cm/sec and OB decreases at the rate of 1 cm/sec, therate of decreases of the area of DeltaAOB after 2 seconds is |
| Answer» Answer :A | |
| 4580. |
Which of the following is not true about the matrix|(1,0,0),(0,0,0),(0,0,5)|? |
|
Answer» a scalar matrix |
|
| 4581. |
If f(x) = x^(n) for 0 lt a lt band na^(n-1) le (b^(n) - a^(n))/( b-a) le nb^(n-1) then n is |
| Answer» Answer :A | |
| 4582. |
Equation to the pair of lines passing through the origin whose sum and product of slopes are A.M. and G.M. of 4 and 9 is |
|
Answer» `12X^(2)-13xy+2y^(2)=0` |
|
| 4584. |
A, B and C are foot of perpendicular from point P(-5, 3, 7) on XY, YZ, ZX planes. Then write coordinates of the point A, B and C. |
|
Answer» |
|
| 4585. |
(5, 2) is the mid point of the line segment intercepted between axes then equation of line is….......... |
|
Answer» `5x + 2Y = 20` |
|
| 4586. |
Statement-I : If f(theta)=(cot theta)/(1+cot theta) and alpha+ beta=(5pi)/(4) then f(alpha) f(beta)=(1)/(2) Statement-II : If alpha+ beta=(pi)/(2) and beta+ gamma= alpha then tan alpha= tan beta+ 2tan gamm Statement-III sin^(2) alpha+ cos^(2) (alpha+ beta)+2 sin alpha beta cos (alpha+beta) is independent of alpha only |
|
Answer» Only, I, II are true |
|
| 4587. |
The smallest value of x^(2)-3x+3 in the interval [-3,(3)/(2)] is |
| Answer» ANSWER :A | |
| 4588. |
If vecbara=2bari+3barj-4bark,vecb=bari+barj+bark,vecc=4bari+2barj+3bark then abs(vecaxx(vecbxxvecc))= |
| Answer» ANSWER :D | |
| 4589. |
The verticle angleof an isosceles triangle is (2)/(3) of each od its base angle. Find it in radians. |
|
Answer» |
|
| 4591. |
The sum of the radii of inscribed and circumscribed circles for an n sided regular polygon of side a, is |
|
Answer» `(a)/(2)COT((PI)/(2N))` |
|
| 4592. |
S-I : If f(x) is odd function and g(x) is even function then f(x)=g(x) is nether even nor odd S-II : Odd function is symmetrical in opposite quadrants and even function is symmetrical about the y-axis |
|
Answer» Statement 1 is true, statement 2 is true, statement 2 is a CORRECT EXPLANATION for statement 1. |
|
| 4593. |
Match the following {:("List-1","List-II"),("(A)D.C's of x-axis",(1)"1,1,1"),("(B) D.C of y-axis",(2) (1)/(sqrt(3))","(1)/(sqrt(3))","(1)/(sqrt(3))),("(C)D.C of z-axis",(3)"1,0,0"),("(D)D.C's of a line which",(4)"0,1,0"), (" makes equal",), ("angles with axes",),(,(5)"0,0,1"):} |
|
Answer» `{:("A,B,C,D),(3,4,5,2):}` |
|
| 4594. |
Simiplify :sqrt(-64).(3 + sqrt(-361)) |
|
Answer» |
|
| 4595. |
If f(x)=sin log, {(sqrt(4-x^(2)))/(1-x)}, then the domain of f(x) is _______ and its range is _ |
|
Answer» R and [0, 1] |
|
| 4596. |
Find the derivativ of the function w.r.to x cos [tan ^(-1) (log x)] |
|
Answer» |
|
| 4597. |
Find the cartesian equation of the curve whose parametric equations are : x=t, y=3t+5 |
|
Answer» |
|
| 4598. |
The sum to infinity of the series 1+2/3+6/3^2+14/3^4+...is |
|
Answer» 6 |
|
| 4599. |
If tan^(-1)((3a^(2)x-x^(3))/(a^(3)-3ax^(2)))=k tan^(-1)(x/a) then k= |
|
Answer» 2 |
|
| 4600. |
If R=([1+((dy)/(dx))^2]^(3/2))/((d^2y)/(dx^2)), then R^(2/3) can be put in the form of |
|
Answer» `1/(((d^2y)/(dx^2))^(2/3))+1/(((d^2x)/(dy^2))^(2/3))` |
|