InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 10452. |
Area of the region bounded by y=e^(x),y=e^(-x) and the line x=1 is |
|
Answer» |
|
| 10453. |
If a_(1), a_(2), ……., a_(n) are in A.P. with common differece d != 0, then (sin d) [sec a_(1) sec a_(2) + sec a_(2) sec a_(3) + .... + sec a_(n - 1) sec a_(n)] is equal to |
|
Answer» a. `COT a_(n) - cot a_(1)` |
|
| 10454. |
Statement 1: The area of the ellipse 2x^(2)+3y^(2) =6 is more than the area of the circlex^(2) +y^(2) -2x +4y +4=0 Statement 2: The length of semi-major axis of an ellipse is more than the radius of the circle. |
|
Answer» Both the statement are True and statement 2 is the correct EXPLANATION of statement 1 |
|
| 10455. |
inte^(x)(cotx-cot^(2)x)dx=.......+c |
|
Answer» `E^(X)COSEC^(2)x` |
|
| 10456. |
If A = ((i,-i),(-i,i)) and B= ((1,-1),(-1,1)) then A^(8) equals |
| Answer» Answer :A | |
| 10457. |
Compute the area contained between the cissoid y^(2)=(x^(3))/(2a-x) and its asymptote. |
|
Answer» |
|
| 10458. |
The solution of (dy)/(dx) = 2xy - 2y + 2x -3 is |
|
Answer» `e^(X^(2) + 3x) = c (y +1)` |
|
| 10459. |
Two rods of different materials having coefficient of thermal expansion alpha_(1)and alpha_(2) and Young's moduli Y_(1) AND Y_(2) respectively are fixed between two rigid massive walls. The rods are heated such that they undergo the same increase in temperature. There is no bending of the rods. If alpha_(1) and alpha_(2) are in the ratio2:3, the thermal stresses i the rods would be same for ratio Y_(1)//Y_(2)= |
| Answer» ANSWER :C | |
| 10460. |
In a bag there are 10 black & 10 white balls. A ball is drawn at random & 5 extra balls of same color as of drawn ball are added in the bag along with drawn ball. Now another ball is drawn and replaced in the bag but 4 balls of color same as drawn ball are removed from the bag. Again a ball drawn and found to be white find the probability that the second drawn ball was black. |
|
Answer» `4/7`  REQUIRED PROBABILITY `(1/2xx15/25xx10/21+1/2xx10/25xx15/21)/(1/2xx15/25xx10/21+1/2xx10/25xx6/21+1/2xx10/25xx15/21+1/2xx15/25xx11/21)` `=2/(1+2/5+1+11/10)=20/(11+20+4)=4/7` |
|
| 10461. |
If f (x,y) =3x ^(2) + 2xy where x = r + 2s ^(2), y = r ^(2) -s find (delf)/(delr), (drl f)/(dels). |
|
Answer» |
|
| 10462. |
A factory owner purchase two types of machines A and B for his factory. The requirements and limitations for the machines are as follows. He has an area of 9000 m^(2) available and 72 skilled persons who can operate the machines. How many machines of each types should he buy to maximise the daily output ? |
|
Answer» |
|
| 10463. |
The scalar vecA. (vecB.vecC)xx(vecA + vecB + vecC)equals |
| Answer» Answer :A | |
| 10464. |
Evaluate int_(0)^(n^(2))[ sqrt(x)] dx ( n in N) where [ ] denotes the GIF |
|
Answer» |
|
| 10465. |
Statement-I : If e^(itheta)=costheta+isintheta then for the DeltaABCe^(iA)e^(iB)e^(iC)=-1Statement-II : If (sqrt3+1)^(100)=2^(99)(a+ib) then b=2sqrt3 |
|
Answer» Only I is true |
|
| 10466. |
Why do emotions such as anger or fear slow digestion :- |
|
Answer» Because they STIMULATE the PARASYMPATHETIC Nerves supplying the GI Tract. |
|
| 10467. |
E and F are mid-points of diagonals AC and BD of squareABCD. If G is the mid-point of seg EF, then |
| Answer» Answer :B | |
| 10468. |
If x is small and if the expansion of a + (b)/(1 + 2x) + ( c)/(1 -3x^2) is 1 + x + 2x^2 + ……oo find (a,b,c) |
|
Answer» |
|
| 10469. |
The number of ways can a collection of 30 books be divided into two groups of 10 and 20 so that the first group always contains a particular book is |
|
Answer» `""^(29)C_(29)` |
|
| 10471. |
The vectors overlin(2i)-overline(3j)+overline(k),i-overline(2j)+overline(3k),overline(3i)+overline(j)-overline(2k) |
|
Answer» are linearly dependent |
|
| 10472. |
If the function f(x)=(sin 3x)/(x)" for "x ne 0 and f(0)=k/2 is continuous at x=0 then k= |
|
Answer» 3 |
|
| 10473. |
Let A = {z: z in C, |z-i| = |z+1|} and B = {z : z in C, |z| =1}, Then |
|
Answer» `A cap B` is a singleton |
|
| 10475. |
What does "The Last Lesson" symbolize? |
|
Answer» Loss |
|
| 10476. |
Evalute the following integrals int sqrt(e^(x) - 4) dx on [ log_(e)^(4), infty) |
|
Answer» |
|
| 10477. |
Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114. Point P(0, lambda) is a point on y-axis such that 0 lt lambda lt 38 " and point " Q(0, lambda) is a point on y-axis such that lambda gt 38. For all positions of pont Q, and AQB is maximum when point Q is |
|
Answer» (0, 54) 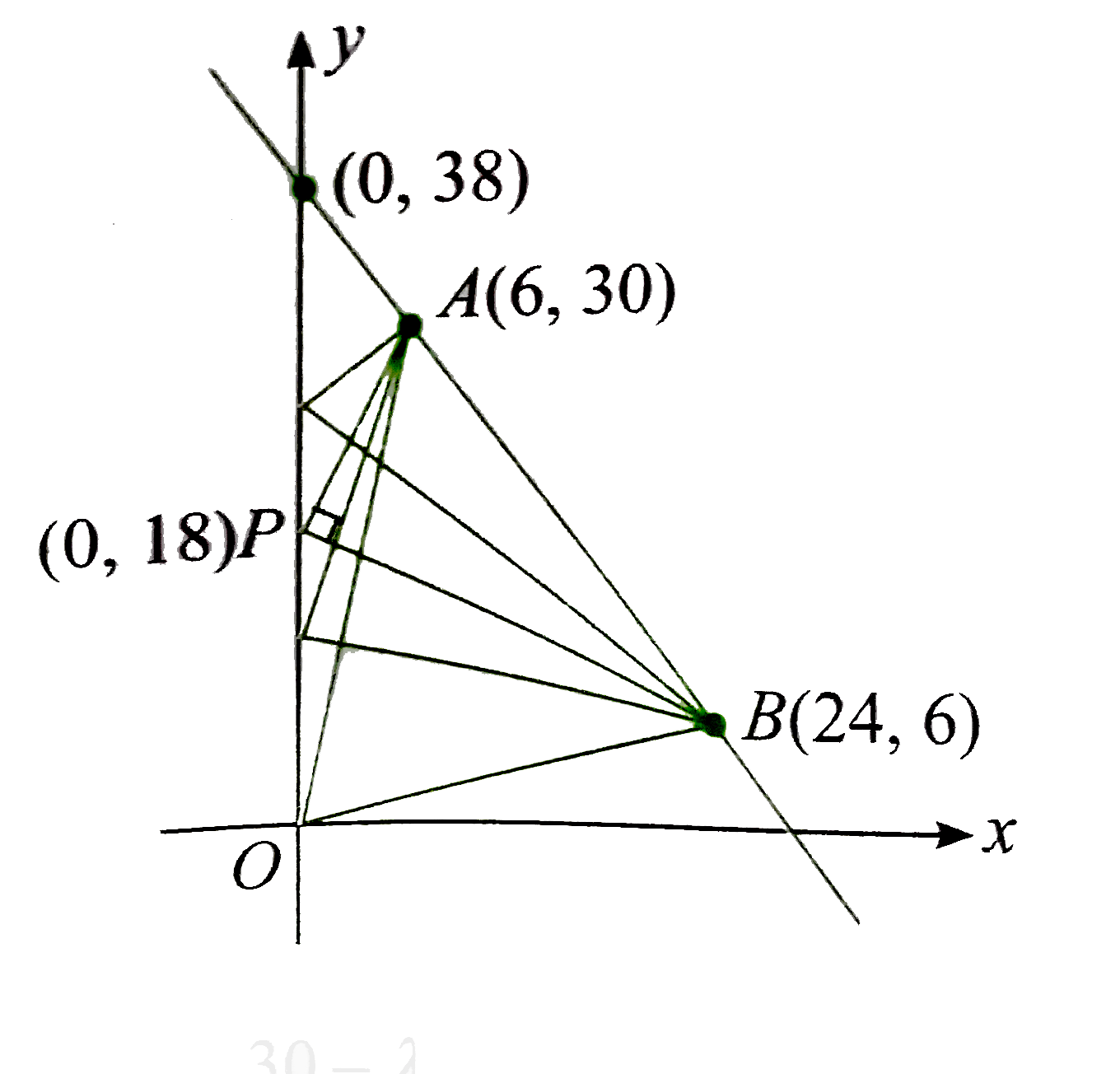 `"Slope of "AP" is "m_(1)= (30-lambda)/(6)` `"Slope of "BP" is "m_(2)= (6-lambda)/(24)` `"TAN"THETA = ((30-lambda)/(6)-(6-lambda)/(24))/(1+((30-lambda)/(6))((6-lambda)/(24)))` `=(720-24lambda-36+6lambda)/(144+180-36lambda+lambda^(2))` `=(18(38-lambda))/(324-36lambda+lambda^(2)) = ((38-lambda)18)/((lambda-18)^(2))` `"Clearly, for "0 lt lambda lt 38.` Maximum value of `"tan" theta to oo " for which " theta = (pi)/(2),` `"Now, " (d)/(dlambda)("tan" theta) = (18(18-lambda)(lambda-58))/((lambda-18)^(4))` `"Clearly, "lambda = 58` is point of maximum as DERIVATIVE changes sign from `'+' " to " '-'`. So, point `Q-=(0,58) " when " angleAQB`is maximum. |
|
| 10478. |
For the plane vec(r).(2hat(i)+3hat(j)+5hat(k))=3 |
|
Answer» the NORMAL vector is `2hat(i)+3hat(j)+5hat(k)` |
|
| 10479. |
Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114. Point P(0, lambda) is a point on y-axis such that 0 lt lambda lt 38 " and point " Q(0, lambda) is a point on y-axis such that lambda gt 38. The maximum value of angle APB is |
|
Answer» `(pi)/(3)` 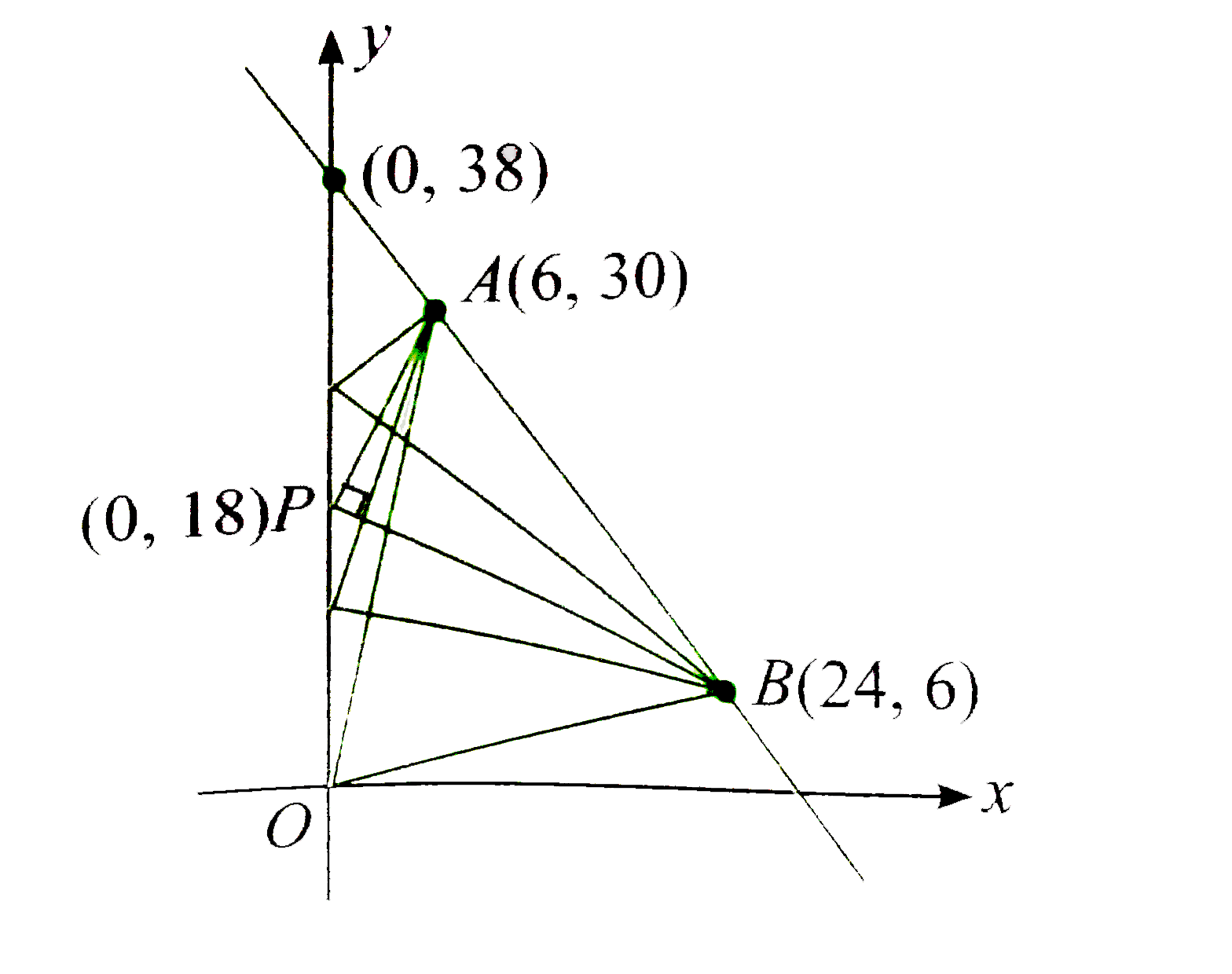 `"Slope of "AP" is "m_(1)= (30-LAMBDA)/(6)` `"Slope of "BP" is "m_(2)= (6-lambda)/(24)` `"tan"theta = ((30-lambda)/(6)-(6-lambda)/(24))/(1+((30-lambda)/(6))((6-lambda)/(24)))` `=(720-24lambda-36+6lambda)/(144+180-36lambda+lambda^(2))` `=(18(38-lambda))/(324-36lambda+lambda^(2)) = ((38-lambda)18)/((lambda-18)^(2))` `"CLEARLY, for "0 lt lambda lt 38.` Maximum value of `"tan" theta to oo " for which " theta = (pi)/(2),` `"Now, " (d)/(dlambda)("tan" theta) = (18(18-lambda)(lambda-58))/((lambda-18)^(4))` `"Clearly, "lambda = 58` is point of maximum as DERIVATIVE changes sign from `'+' " to " '-'`. So, point `Q-=(0,58) " when " angleAQB`is maximum. |
|
| 10480. |
Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114. Point P(0, lambda) is a point on y-axis such that 0 lt lambda lt 38 " and point " Q(0, lambda) is a point on y-axis such that lambda gt 38. For all positions of pont P, angle APB is maximum when point P is |
|
Answer» (0, 12)  `"Slope of "AP" is "m_(1)= (30-LAMBDA)/(6)` `"Slope of "BP" is "m_(2)= (6-lambda)/(24)` `"tan"THETA = ((30-lambda)/(6)-(6-lambda)/(24))/(1+((30-lambda)/(6))((6-lambda)/(24)))` `=(720-24lambda-36+6lambda)/(144+180-36lambda+lambda^(2))` `=(18(38-lambda))/(324-36lambda+lambda^(2)) = ((38-lambda)18)/((lambda-18)^(2))` `"Clearly, for "0 lt lambda lt 38.` Maximum value of `"tan" theta to oo " for which " theta = (pi)/(2),` `"Now, " (d)/(dlambda)("tan" theta) = (18(18-lambda)(lambda-58))/((lambda-18)^(4))` `"Clearly, "lambda = 58` is point of maximum as derivative changes sign from `'+' " to " '-'`. So, point `Q-=(0,58) " when " angleAQB`is maximum. |
|
| 10481. |
For the following probability distribution E(X^(2)) is equal to ....... |
|
Answer» 3 |
|
| 10482. |
Locus of centroid of the triangle whose vertices are (a cost, a sint), (b sint,b cost) and (1, 0), where t is a parameter, is |
|
Answer» `(3x-1)^(2)+(3Y)^(2)=a^(2)+B^(2)` |
|
| 10483. |
If y=mx+6is a tangent to both the parabolas y^2=8xand x^2=3by , thenbis equal to : |
|
Answer» 36 So, `6=2/m rArr m=1/3` Now `y=x/3+6` is tangent to `x^2=3by` `rArr x^2=(3b)/(x/3+6)` `x^2=bx+18b` `x^2-bx-18b=0` D=0 `B^2=4 XX (-18) b^2 (b NE 0)` b=-72 |
|
| 10484. |
If the line 2x+5y=12 intersect the ellipse 4x^(2)+5y^(2)=20 in two distinct point A and B, then mid-point of AB is, |
|
Answer» (0,1) |
|
| 10485. |
Eachof thefivequestionsin a multiplechoicetesthas4possibleanswer. Thenumberof differentsetsof possibleanswersis |
| Answer» Answer :C | |
| 10486. |
Find thearea of theregionboundedby theparbolay^2 =xandlinex+y=2 |
|
Answer» |
|
| 10487. |
Find the value of sum_(i=1)^n sum_(i=1)^n sum_(k=1)^n 1 |
|
Answer» |
|
| 10488. |
The sum of the maximum and the minimum values of 3x^(4)-2x^(3)-6x^(2)+6x+4, in (0, 2) is |
|
Answer» 28 |
|
| 10489. |
Let P={theta:sin theta-cos theta=sqrt(2)cos theta} and Q={theta :sin theta+cos theta=sqrt(2)sin theta} be two sets. Then |
|
Answer» `P sub Q` and `Q-P NE PHI` |
|
| 10490. |
Evaluate the following integrals. int(1)/((x^(2)_a^(2))(x^(2)+b^(2)))dx |
|
Answer» |
|
| 10491. |
If l and b are respectively the length and breadth of the reactangle of greatest area that can be isscribed in the ellipse x^(2)+4y^(2)=64 then (l,b)= |
|
Answer» `(16sqrt(2),4sqrt(2))` |
|
| 10492. |
If 5 boys and 5 girls sit in a row at random what is the prbability that no two of the same sex come together. |
|
Answer» |
|
| 10493. |
Evaluate the following integrals: int_0^(pi/2) cos^2x dx |
|
Answer» Solution :`int_0^(pi/2) cos^2x DX` =`int_0^(pi/2) (1+cos 2x)/2 dx = 1/2[x+(SIN2X)/2]_0^(pi/2)` =`1/2 ((pi/2+0)-(0+0)) = pi/4` |
|
| 10494. |
For which value of a, A function,f(x)=x^(3)+3(a-7)x^(2)+3(a^(2)-9)x-1attains its maximum value point. |
|
Answer» |
|
| 10495. |
Find a if f(x)={((sqrt(5x+2)-sqrt(4x+4))/(x-2),x!=2),(a,x=2):} is continuous as x=2 |
|
Answer» 1/(2SQRT3) |
|
| 10496. |
Find the area enclosed by the ellpise x^(2)/a^(2) + y^(2)/b^(2) = 1 |
|
Answer» |
|
| 10500. |
The maximum electric field at a point on the axis a uniformly charged ring is E_(0). At how many points on the axis will be magnitude of electric field be E_(0)//2 |
|
Answer» 1 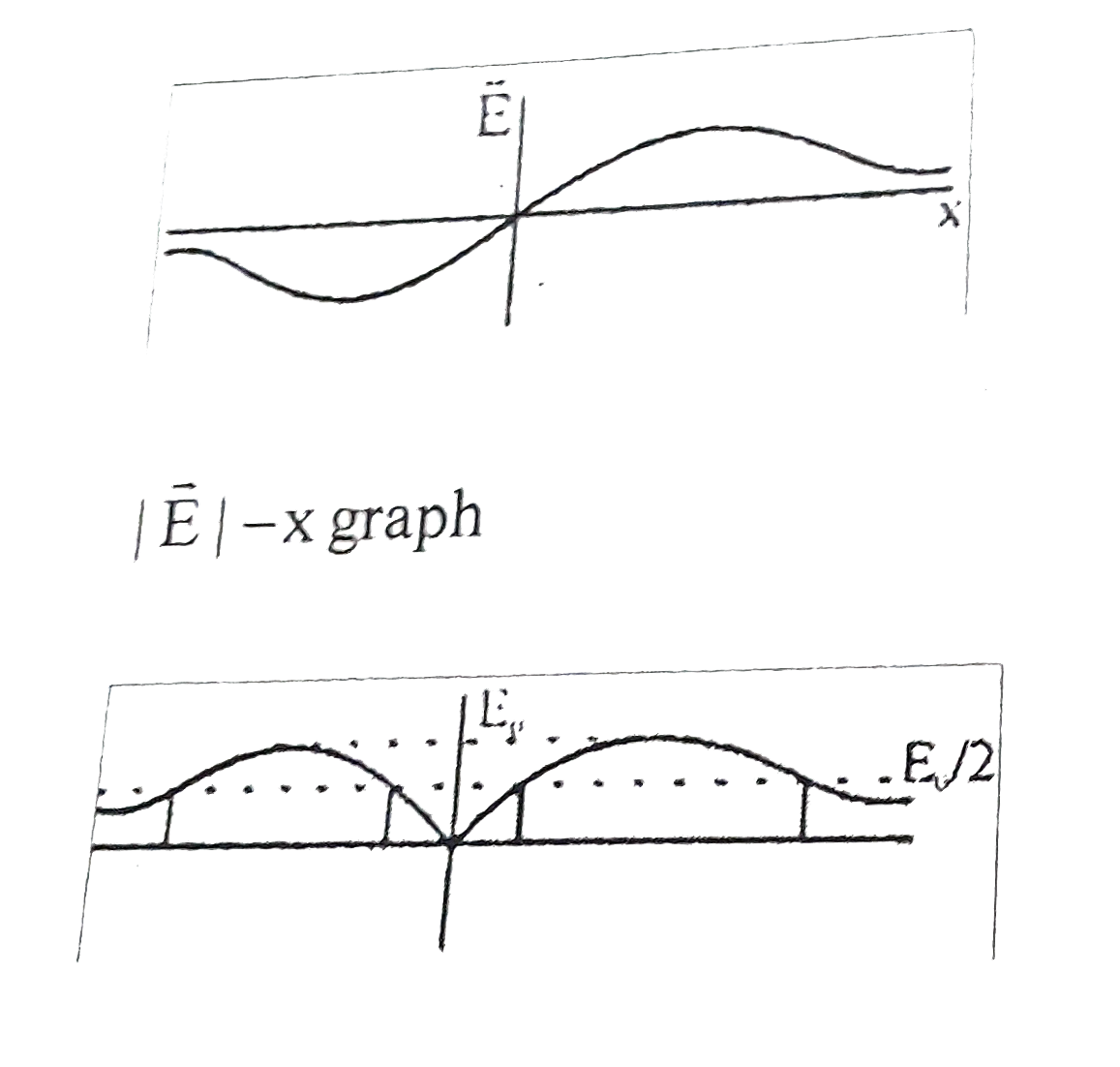
|
|