InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 10501. |
A new sequence is obtained from the sequence of positive integers 1,2,…….., by deleting all the perfect squares. What is the 2015th term from the beginning of the new sequence ? |
|
Answer» |
|
| 10502. |
A black and red dice are rolled. a. Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5. b. Find the conditional probability of obtainingthe sum 8, given that the red die resulted in a number less than 4. |
|
Answer» |
|
| 10503. |
Solve the differential equation dy/dx=1+x+y^(2)+xy^(2) , when y=0, x=0 |
|
Answer» |
|
| 10504. |
If alpha and beta are the roots of the equation ax^(2)+bx+c=0then (alpha+beta)^(2) is ………….. |
| Answer» ANSWER :D | |
| 10505. |
If int(cos^(2)xsinx)/(sinx-cosx)dx=A log|sinx-cosx|+(1)/(8)(sin2x+cos2x)+C then A is equal to. |
|
Answer» |
|
| 10506. |
The n ^(th) terms of the series 1 + (4)/(5) + (7)/(5 ^(2)) + (10)/(5 ^(3)) +………. is |
|
Answer» |
|
| 10507. |
Prove that the curves y^(2)=4x and x^(2)+y^(2)-6x+1=0 touch each other at the point (1, 2). |
|
Answer» |
|
| 10508. |
If a, b and c are three positive real numbers such that a+bgec, then |
|
Answer» `(a)/(1+a)+(b)/(1+b)ge(C)/(1+c)` |
|
| 10509. |
Show that the function f defined as follows, is continuoius at x=2, but not differentiable at x=2. f(x)={{:(3x-2, 0 lt x le 1),(2x^(2)-x, 1 lt x le 2),(5x-4,x gt 2):}. |
|
Answer» |
|
| 10510. |
The value of int_(0)^(1)(8log(1+x))/(1+x^(2))dx is : |
|
Answer» `(pi)/(8) log2` |
|
| 10511. |
The value of int_(0)^(1) (x^( 2 alpha) - 1)/( log x) dx, if alpha = (2n-1)/( 2) is |
|
Answer» `log n` |
|
| 10512. |
A person has undertaken a construetion job. The probabilities are 0.65 that there will be strike, 0.80 that the construction job will be completed on time it there is no strike and 0.32 that the construction job will be completed on time if there is a strike. Determine the probability that the construction job will be completed on time. |
|
Answer» |
|
| 10513. |
Solve the following system of equation by using matrix method : x+y+z=6, y+3z-11=0" and "x+z=2y. |
|
Answer» |
|
| 10514. |
On the xy plane where O is the origin, given points, A(1,0), B(0,1) and C(1,1). Let P,Q, and R be moving points on the line OA, OB, OC respectively such that vec(OP)=45t(vec(OA)), vec(OQ)=60t(vec(OB)), vec(OR)=(1-t)(vec(OC)) with t gt 0. If the three points P,Q and R are collinear then the value of t is equal to |
|
Answer» `1/106` `rArr vec(PQ) = lambdavec(QR)` `rArr 15R(4vecj-3veci)=LAMBDA[(1-t)(HATI+hatj)-60thatj]` `=lambda[(1-t)hati+(1-6lthatj)]` `rArr (45t)/(t-1) = (4t)/(1-61t)` `rArr 3(1-61t)=4(t-1)` `rArr 3-183t=4t-4` `rArr 187t=7` `rArr t=7/187` |
|
| 10515. |
If (2,-1,3) is the foot of the perpendicular drawn from the origin to the plane , then the equation of the plane is |
|
Answer» `2x+y-3Z+6=0` |
|
| 10516. |
Discuss the continuity of the function f, where f is defined by f(x)={{:(2x," if "x lt 0),(0," if "0 le x le 1),(4x," if "x ge 1):}. |
|
Answer» |
|
| 10517. |
If m_1, m_2, are slopes of the tangens to the hyperbola x^(2)//25-y^(2)//16=1 which pass through the point (6, 2) then |
|
Answer» `m_(1)+m_(2)=24//11` |
|
| 10518. |
Find values of k if area of triangle is 4 sq. units and vertices are ( i) (k,0),(4,0) ,( 0,2) "(ii) " ( -2,0),( 0,4),( 0,k ) |
|
Answer» |
|
| 10519. |
If in the triangleABC, B = 45^@, thena^4+ b^4 +c^4 = |
|
Answer» `2a^2( b^2+ C^2)` |
|
| 10520. |
If two members of family (2+lambda)x+(1+2lambda)y-3(1+lambda) = 0 and line x+y=0 make an equilateral triangle, the the incentre of triangle so formed is |
|
Answer» `((1)/(3), (1)/(3))` `(2x+y-3)+lambda(x+2y-3) =0, lambda in R.` The family of lines is concurrent at point of intersection of 2x+y-3 = 0 and x+2y-3=0 which is A(1,1). Two members `L_(1)" and "L_(2)` of this family and line x+y=0 form an equilateral TRIANGLE. Let foot of perpendicular from A(1, 1) on the line x+y=0 be M(h,K). `(h-1)/(1) = (k-1)/(1) = (-(1+1))/(2)` `therefore M-=(h,k)-=(0,0)` SINCE triangle is equilateral, AM is median, altitude and angle bisector. `AM= sqrt((1-0)^(2)+(1-0)^(2)) = sqrt(2)` Incentre coincides with centroid G such that AG `=(2)/(3)sqrt(2)`. `"Slope of " AM is 1 = "TAN" 45^(@)`. `therefore G-=(1-(2sqrt(2))/(3)"cos" 45^(@), 1-(2sqrt(2))/(3)"sin" 45^(@))` `-=((1)/(3),(1)/(3))` |
|
| 10521. |
If f(x)=sin^(-1)[e^(x)]+sin^(-1)[e^(-x)] then which of the following hold(s) good ? [Note: where [k] denotes the larest integer than or equal to k.] |
|
Answer» f(x) has isolated POINT remonable discontinuity at x=0 `e^(x)in(0,2)ande^(-x)in(0,2)` `:.x in(-ln2,ln2)` `"Now,"f(x)={:[(pi,,,x-0),((pi)/(2)",",,,x in(-ln2,ln2)-{0}):}` |
|
| 10522. |
Find the differential equation of the family of (i) all non vertical lines in a plane (ii) all non horizontal lines in aplane |
|
Answer» (II) 0 |
|
| 10523. |
Let a_(m)=underset("m times")(underbrace(111...1)), then which of the following is a prime number ? |
| Answer» Answer :B | |
| 10524. |
LetP(n)be thestatementn^2-n- 41is prime , thenwhich of thefollowingis nottrue ? |
| Answer» Answer :C | |
| 10525. |
Find the area of the parallelogram whose diagonals are represented by -2hati+4hatj+4hatk and -4hati-2hatk |
|
Answer» |
|
| 10526. |
If x^2 + 2x + n gt 10 for all real number x, then which of the following conditions is true ? |
| Answer» Answer :D | |
| 10527. |
For events A and B P(bar(A cup B))= (1)/(6), P(barA)= (1)/(4) and P(A cap B) = (1)/(4) , Where (barA) is the complementary event of A then events A and B are |
|
Answer» INDEPENDENT but not equiprobable |
|
| 10528. |
Solve system of linear equations, using matrix method in examples 7 to 14 5x+2y=4 7x+3y=5 |
|
Answer» |
|
| 10529. |
If the vectors bara = 3hati +2hatj +9hatk and hatb=hati+ mhatj + 3hatk are parallel then m is………… . |
|
Answer» |
|
| 10530. |
If P= |(x,1),(1,x)| and Q= |(x,1,1),(1,x,1),(1,1,x)| " then " (dQ)/(dx)= _______ |
| Answer» ANSWER :A | |
| 10531. |
Let W denotethe words in the englishdicitionary define the relation R by R: {(x,y) in W xxWIthe words x and y have at least one letter in common }Then R is |
|
Answer» REFLEXIVE, SYMMETRIC and not TRANSITIVE |
|
| 10532. |
Prove that .^(n)C_(1) + 2 xx .^(n)C_(2) + 3 xx .^(n)C_(3) + "…." + n xx .^(n)C_(n) = n2^(n-1). Hence, prove that .^(n)C_(1).(.^(n)C_(2))^(2).(.^(n)C_(3))^(3)"......."(.^(n)C_(n))^(n) le ((2^(n))/(n+1))^(.^(n+1)C_(2)) AA n in N. |
|
Answer» Solution :Method I : `.^(N)C_(1) + 2.^(n)C_(2)+3.^(n)C_(3)+"….."+n.^(n)C_(n)` `=underset(R=1)overset(n)sumr.^(n)C_(r)` `= n underset(r=1)overset(n)sum.^(n-1)C_(r-1)` `= n(.^(n-1)C_(0) + .^(n-1)C_(1) + .^(n-1)C_(2) + .^(n-1)C_(3)+"…."+.^(n-1)C_(n-1))` `= n2^(n-1)` Method II : We have `(1+x)^(n) = .^(n)C_(0) + .^(n)C_(1)x+.^(n)C_(2)x^(2)+"...."+.^(n)C_(n)x^(n)` Differentiatingw.r.t x, we get `n(1+x)^(n-1)= .^(n)C_(1)+2 xx .^(n)C_(2)x + 3 xx .^(n)C_(3)x^(2) +"......" + n xx .^(n)C_(n)x^(n-1)` PUTTING `x = 1`, we get `n2^( n-1) = .^(n)C_(1)+2xx .^(n)C_(2) + "....." + n xx .^(n)C_(n)` USING `A.M. ge G.M.`, we get `(.^(n)C_(1)+2.^(n)C_(2)+3.^(n)C_(3)+".....+n.^(n)C_(n))/((n(n+1))/(2))` `[(.^(n)C_(1))(.^(n)C_(2))^(2)(.^(n)C_(3))^(3)"....."(.^(n)C_(n))^(n)]^((1)/((pi(n-1))/2))` `rArr (n2^(n-1))/((n(n+1))/(2))ge [(.^(n)C_(1))(.^(n)C_(2))^(2)(.^(n)C_(3))^(3)"....."(.^(n)C_(n))^(n)]^((2)/(n(n+1)))` `(.^(n)C_(1))(.^(n)C_(2))^(2)(.^(n)C_(3))^(3)"....."(.^(n)C_(n))^(n)le((2^(n))/(n+1))^((n(n+1))/(2))` or`(.^(n)C_(1))(.^(n)C_(2))^(2)(.^(n)C_(3))^(3)"....."(.^(n)C_(n))^(n)le((2^(n))/(n+1))^(.^(n+1)C_(2))` |
|
| 10533. |
Two friends A and B have equal number of daughters of A and B . The probability that all the tickets go to daughters of A is 1/20.The number of daughters each of them have is |
|
Answer» 4 |
|
| 10534. |
If the ellipse x^(2)+k^(2)y^(2)=k^(2)a^(2) is confocal with the hyperbola x^(2)-y^(2)=a^(2), then match the following lists and choose the correct code. |
|
Answer» and Focus of hyperbola `-=(ae_(2),0)` Now, `kae_(1)=ae_(2)` `rArr""sqrt(1-(a^(2))/(k^(2)a^(2)))=sqrt(1+(a^(2))/(a^(2)))` `rArr""k^(2)-1=2` `therefore""k= pmsqrt3` a. `(e_(2))/(e_(1))=k=SQRT3` ltBrgt b. Major axis of ellipse = 2ka and Transverse axis of hyperbola = 2A `therefore""(2ka)/(2a)=k=sqrt3` C. Since curves are confocal, they are orthogonal. `therefore""theta=(pi)/(2)` d. Latus rectum of ellipse and hyperbola are`(2a^(2))/(ak) and (2a^(2))/(a)`, respectively. `therefore""(2a//k)/(2a)=(1)/(k)=(1)/(sqrt3)` |
|
| 10535. |
A certain coin is tossed with probability of showing head being 'p'. Let 'q' denotes the probability that when the coin is tossed four times the number of heads obtained is even. Then |
|
Answer» there is no value of `p`, if `q=(1)/(4)` `:.q=p^(4)+^(4)C_(2)p^(2)(1-p)^(2)+(1-p)^(4)` `=8p^(4)-16p^(3)+12p^(2)-4p+1` `=((2p-1)^(4)+1)/(2)` Now put the values and check. |
|
| 10536. |
Let f: (-oo, oo) rarr (-oo, oo) be acontinuous and differentiable function and let f'(.) denote the derivative of f(.).If f(0) = -2 and f'(x) le 3 for each x in [0, 2], then the largest possible value of f(2) is |
|
Answer» 1 |
|
| 10537. |
Construct truth tables for the following and indicate which of these are tautologies [p rarr ( p vv q)] rarr [q rarr (p ^^ q)] |
Answer» SOLUTION :
|
|
| 10538. |
The midpoint of chord formed by the polar of (-9,2) w.r.t x^(2)+y^(2)=100 is |
|
Answer» `(4,-4/3)` |
|
| 10539. |
The solution of (dy)/(dx) + (1)/(x) = (e^(y))/(x^(2)) is |
|
Answer» `2X = (1+Cx^(2))E^(y)` |
|
| 10540. |
A family of curve S is given by S -= x^(2) +2xy +y^(2)-4x(1-lambda) - 4y (1+lambda) +4, then S = 0 represents |
|
Answer» pair of straight LINE `AA lambda in R` `rArr (x+y-2)^(2) = 4 lambda (y-x)` If `lambda=0`, it represents pair of straight line otherwise parabola. |
|
| 10541. |
If 8x+5y le 40, 4x+3y ge 12, x ge 0, y ge 0 then the maximum value of f=3x+2y is |
|
Answer» 5 |
|
| 10542. |
If 6 letters are placed at random in 6 addressed envelopes. Then the odds in favour of arranging them such that no letter goes into correct envelope is |
|
Answer» `53 : 91` |
|
| 10543. |
The transformed equation of x^(5) + 5x^(4) + 3x^(3) + x^(2) + x -1 = 0 , by eliminating second terms is |
|
Answer» `y^(5) - 7Y^(3) + 12y^(2) - 7y = 0` |
|
| 10544. |
If the volume of the tetrahedron with edges 2i + j -k, I + aj + k and I + 2j - k is one cubic unir then a = |
| Answer» ANSWER :C | |
| 10545. |
Two tangents are drawn from any point P on a given line L=0 to a given circle S=0, if these tangents touch the circle at point A and B, then locus of the circumcentre the DeltaPAB will be |
|
Answer» A pair of straight lines 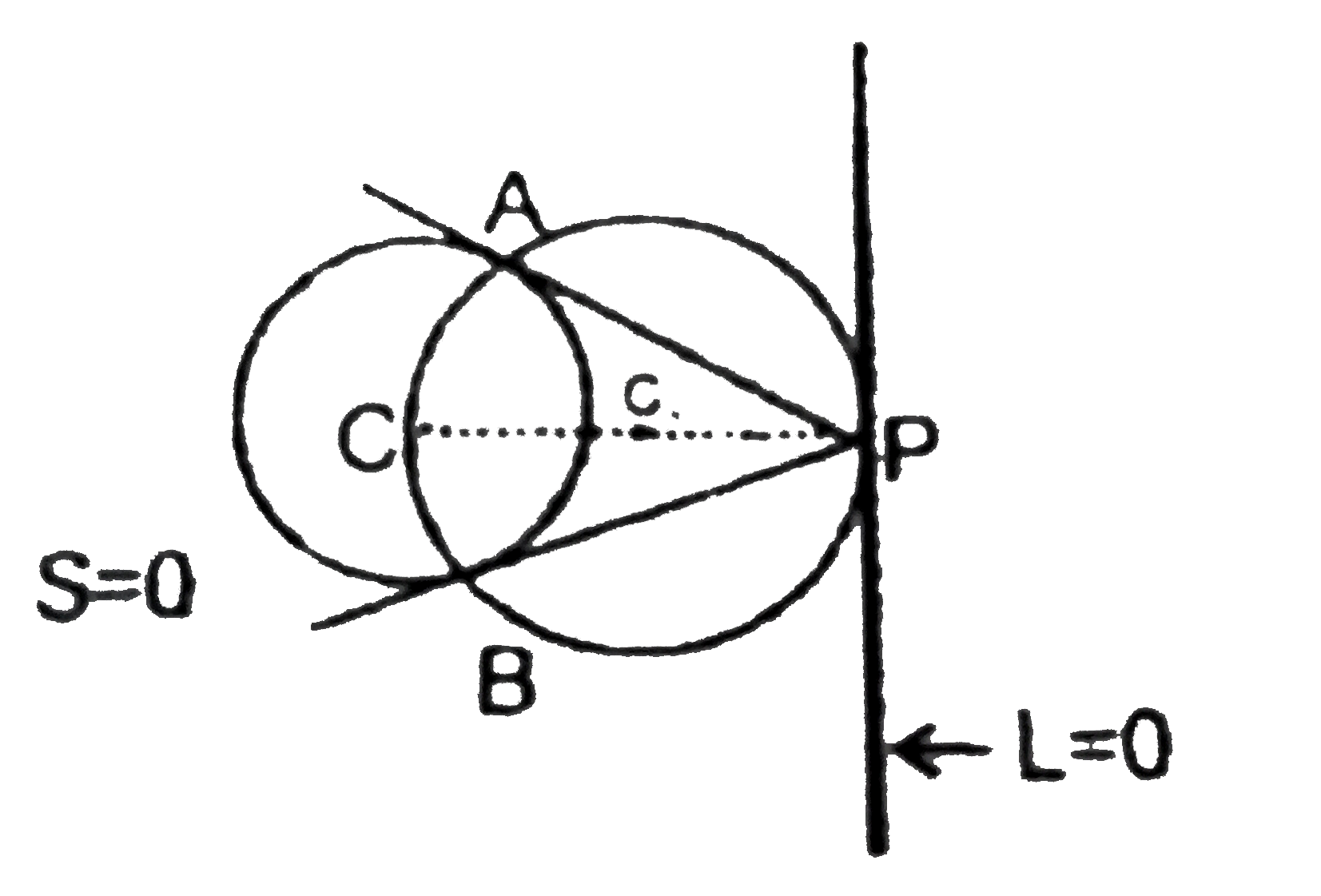 The circumcirle of `DeltaPAB` PASSES through C with PC as its diameter. Therefore centre of this circle `(C_(1))` will be MID pt of PC. Let `L=ax+by+c=0` `P(x_(1).y_(1)) & C(p,q)` `C_(1)(H,k)` `h=(x_(1)+p)/(2)` `k=(y_(1)+q)/(2)` `p(x_(1),y_(1))` passes through `L=0` `impliesax_(1)+by_(1)+c=0` or `a(2h-p)+b(2k-q)+c=0` or `2ah+2bk-ap-bq+c=0` Locus of `(h,k)` is `ax+by=(ap+bq+c)/(2)` `implies` A line parallel to `L=0` |
|
| 10546. |
Prove the inequalities : (a) 202^(303) gt 303^(202) (b) 202! Lt 100^(2000 |
|
Answer» |
|
| 10547. |
Let f:RRrarrRR be a continuous function defined defined by f(x)=(1)/(e^(x)+2e^(-x)) Statement - I : f(c)=(1)/(3)"for some "c inRR Statement - II 0ltf(x)le(1)/(2sqrt(2))" for all "x in RR |
|
Answer» Statement -I is True , Statement -II is True , Statement -II is a CORRECT explanation for statement -I |
|
| 10548. |
The centre of the ellipse (x+y-2)^(2)/9+(x-y)^(2)/16=1 is |
|
Answer» |
|
| 10549. |
The value I= int_(-1)^(1) ( cos^(-1) x + (x^(7) -3x^(5) + 7x^(3) -x) /( cos ^(2) x ) ) dx is |
| Answer» ANSWER :D | |
| 10550. |
4 moles of H_(2) at 500 K is mixed with 2 moles of He at 400 K. The mixture attains a temperature T and volume V. Now the mixture is compressed adiabatically to a volume V' and temperature T'. If (T')/T=(V/(V'))^(n), find the value of 26 n. |
|
Answer» |
|