InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 10801. |
If sum_(k = 1)^(n) k (k + 1)(k - 1) = pn^(4) + qn^(3) + tn^(2) + sn where p, q, t and s are constants, then the value of s is equal to |
|
Answer» `-1/4` |
|
| 10803. |
If the volume of the parallelopiped whose edges are represented by 12i + lambdak, 3j = k, 2i + j - 15K is 546 then lambda = |
|
Answer» 1 |
|
| 10804. |
Find a vector in the direction of vector 5hat(i)-hat(j)+2hat(k) which has magnitude 8 unit. |
|
Answer» |
|
| 10805. |
Evaluate int_(0)^(n^(2))[sqrt(x)] dx(n in N) where [] denotes the GIF |
|
Answer» |
|
| 10806. |
Integrate the functions 1/(sqrt9sin^(3)xsin(x+alpha)) |
|
Answer» |
|
| 10807. |
Integrate the following int((sec^(-1)x)^2dx)/(xsqrt(x^2-1) |
|
Answer» Solution :`INT((sec^(-1)x)^2dx)/(xsqrt(x^2-1)` [PUT`sec^(-1)x=t then `DX/(xsqrt(x^2-1))=DT` `intt^2dt` `(/3)t^3+C=(1/3)(sec^(-1)x)^3+C` |
|
| 10808. |
Let a ox b =(-2a-b)^2 for all integers a and b . Which of the following is the value of -5 ox 3 ? |
| Answer» Answer :C | |
| 10809. |
Let a die be weighed in such a way that the probability of getting a numbern is proportional to n .Find the probability of each elementary event. |
|
Answer» `P(4)=4/21, P(5)=5/21, P(6)=6/21` |
|
| 10810. |
Differentiate the following w.r.t. x: sin (tan^(-1) e^(-x)) |
|
Answer» |
|
| 10811. |
int(cos2x)/(sin^2x xxcos^2x)dx |
|
Answer» SOLUTION :`INT(COS2X)/(sin^2x xxcos^2x)DX` =`int(cos^2x-sin^2x)/(sin^2x:cos^2x)dx` =`int(cosec^2x-sec^2x)dx` =`-cotx-tanx+C` |
|
| 10812. |
Correct statement about inductive effect is : |
|
Answer» It is a temporary effect |
|
| 10813. |
Find the equation of a plane which bisects perpendicularly the line joining the points A(2, 3, 4) and B(4, 5, 8) at right angles. |
|
Answer» |
|
| 10814. |
There are two types of fertilisers F_(1)" and "F_(2). F_(1) consists of 10% nitrogen and 6% phosphoric acid and F_(2) consists of 5% nitrogen and 10% phosphoric acid. After testing the oil conditions, a farmer finds that she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F_(1) costs Rs. 6/kg and F_(2) costs Rs. 5/kg, determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost ? |
|
Answer» The FERTILISERS CONSISTS 100 kg of `F_(1)` type and 80 kg of `F_(2)` type. |
|
| 10816. |
Let ** be a binary operation on the set Q of rational numbers as follows : a "*" b = a^(2) +b^(2) Find which of the binary operations are commutative and which are associative. |
|
Answer» |
|
| 10817. |
int(tanx+cotx)^2dx |
|
Answer» Solution :`INT(tanx+cotx)^2dx` =`int(sinx/cosx+cosx/sinx)^2dx` =`int((sin^2x+cos^2x)/(cosxsinx))^2`DX =`int1/(sin^2xcos^2x)dx` =`int(sin^2x+cos^2x)/(sin^2xcos^2x)` `int(sec^2+cosec^2)dx=tanx-cotx+C` |
|
| 10818. |
If a fair coin is tossed 6 times, find the probability that you get just one head. |
|
Answer» SOLUTION :A FAIR coin is tossed 6 times. `therefore absS=2^6` The six mutually exclusive events are HTTTTT, THTTTT, TTHTTT, TTTHTT, TTTTHT, TTTTTH. `therefore` PROBABILITY of getting just ONE HEAD `=6/2^6` |
|
| 10819. |
Let vec(a)=hat(i)+2hat(j)+hat(k),vec(b)=hat(i)-hat(j)+hat(k)andvec(c)=hat(i)-hat(j)-hat(k). A vector in the plane of vec(a)andvec(b) whose projection on vec(c)" is "(1)/(sqrt(3)), is |
|
Answer» `4hat(i)-HAT(j)+4hat(k)` |
|
| 10820. |
Expand the expression (1 - x + x^(2))^(4) |
|
Answer» |
|
| 10821. |
Let A=[a_(ij)] and B=[b_(ij)] be two 4xx4 real matrices such that b_(ij)=(-2)^((i+j-2))a_(ji) where i,j=1,2,3,4. IfA is scalar matrix of determinant value of1/128 then determinant of B is |
|
Answer» 64 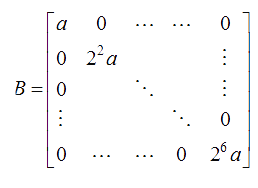 `RARR"det"B=2^(12)a^(4)=2^(12)xx1/128=32` `RARR"det"B=2^(12)a^(4)=2^(12)xx1/128=32`
|
|
| 10822. |
If 7theta=(2n+1)pi, where n=0,1,2,3,4,5,6, thenanswer the following questions. The equations whose roots are cos. (pi)/(7), cos. (3pi)/(7), cos. (5pi)/(7) is |
|
Answer» `8x^(2)+4X^(2)+4x+1=0` |
|
| 10823. |
Triangle triangleACE, shown in the figure below, is isosceles with base bar(AE). B lies on bar(AC) and D lies on bar(CE) . Segments bar(BE) and bar(AD) bisect angleAEC and angleCAE, respectively. Which one of the following angle congruences is necessarily true ? |
|
Answer» `ANGLECAE CONG angleBEC` |
|
| 10824. |
Evaluate the limit . underset(n to 00)("lim") underset(i=1)overset(n)sum (i^(3))/(i^(4)+n^(4)) |
|
Answer» |
|
| 10825. |
int_(0)^(pi//4) (sin^(2) x cos^(2) x)/((sin^(3) x + cos^(3)x)^(2))dx= |
|
Answer» `1/3` |
|
| 10826. |
If one ticket is randomly selected from tickets numbered 1 to 30. Then find the probability that the number on the ticket is. i) a multiple of 5 or 7 ii) a multiple of 3 or 5 |
|
Answer» (B) `(7)/(15)` |
|
| 10827. |
Two circles with radii r_(1) and r_(2), r_(1)gtr_(2)ge2 touch others externelly. If alpha is the angle between direct common tangents then "sin"(alpha)/2=(r_(1)-r_(2))/(r_(1)+r_(2)) |
|
Answer» |
|
| 10828. |
1+(omegax)/(1!) +(omega^2x^2)/(2!)+(omega^3x^3)/(3!)+(omega^4x^4)/(4!)+(omega^5x^5)/(5!)+ .....oo = |
| Answer» Answer :B | |
| 10830. |
Determine the degree of the differential equation(1+((dy)/(dx))^(2))^((3)/(2)) = 5(d^(2)y)/(dx^(2)).Also state the equation is linear or non-linear. Justify your answer. |
|
Answer» |
|
| 10831. |
Using integration, find the area enclosed between the curve y^(2) =2x+1, and the x-y-1=0 |
|
Answer» |
|
| 10832. |
The sum of three numbrs is 6. If we multiply third number by 3 and add second number to itm we get 11 . By adding first and thrid numbers, we get double of the second number. Represent it algebraically and find the number using matrix method |
|
Answer» |
|
| 10833. |
If (2 - i)/((1 - 2i)^(2)) and (-(x + 11i))/(25) are conjugate complex numbers , then x = |
|
Answer» 2 |
|
| 10834. |
A: underset(x to 0)"Lt" (sin (x^(2))/(x)=pi/200 R: underset(x to 0)"Lt" (sin (ax))/(x)=a" if x is measured in radains" |
|
Answer» Both A and R are true and R is the correct explanation of A |
|
| 10835. |
Let M_(n)=[m_("ij")] denotes a square matrix of order n with entries as follows for 1 le i le n, m_(ii)=10, for 1le i le n-1,m_(i+1,i)=m_(i+i+1)=3 and other entries in M_(n) are zero. Let D_(n) be the determinant of matrix of matrix M_(n), then find the value of (D_(3)-9D_(2)) |
|
Answer» 0 |
|
| 10836. |
Given that the events A and B are such that P(A)=1/2,P(AnnB)=3/5 and P(B) =P.Find p if they are independent. |
|
Answer» <P> Solution :Since A and B are INDEPENDENT,`P(AnnB)` |
|
| 10837. |
Let P be a variable point on the ellipse (x^(2))/(25)+(y^(2))/(16)=1with foci at S and S'. Then find the maximum area of the triangle SPS' |
|
Answer» |
|
| 10838. |
Find (i) int cos^(2)x,dx (ii) int sin (2x)cos (3x)dx, (iii) int sin^(3)x dx. |
|
Answer» (ii) `-(1)/(10)cos (5X)+(1)/(2)cosx+c` (iii) `-(3)/(4) cos x+(1)/(12) cos(3x)+c` |
|
| 10839. |
Let f(x)=(log(1+x+x^(2))+log(1-x+x^(2))/(sec x-cos x),x ne 0. Then the value of f(0) so that f is continuos at x=0 is |
|
Answer» 1 |
|
| 10840. |
Each of the roots of the equation x^(3)-6x^(2)+6x-5=0 are the increased by h so that the new transformed equation does not contain x^(2) term, then 'h' is equal to |
|
Answer» 1 |
|
| 10841. |
Find derivatives of the following function.x^(sin x) |
|
Answer» SOLUTION :`y=X^(SINX)` rArrIn y =SIN xcdotIn x` `rArr1/ydy/dx=cosxIn x+sinxcdot1/x` `rArrdy/dx=x^(sinx)(cosxcdotIn x+(sinx)/x)` |
|
| 10842. |
If a chord of the circle x^(2)+y^(2)=16 makes equal intercepts of length a on the co ordinates axes then |a|lt |
|
Answer» `SQRT(2)` |
|
| 10843. |
Prove that a sinA - b sinB = c sin(A-B) |
|
Answer» Solution :R.H.S = c SIN (A-B) = 2R sinC sin (A-B) 2R sin (A+B) sin (A-B) `[THEREFORE A + B + C = pi` or `A + B = pi - C` or sin (A + B) = sin (pi-C) sinC] = 2R `(sin^2A - sin^2B)` = 2R sinA sinA - 2R SINB sinB a sinA - b sinB = L.H.S |
|
| 10844. |
If int sin ^(-1) ( sqrt((x)/(a + x)))dx =A (x)+ constant, then A (x) = |
|
Answer» `a TAN ^(-1) sqrt((X)/(a)) + AX` |
|
| 10845. |
Each of the roots of the equation x^(3) - 6x^(2) + 6x - 5 = 0 are increased by k so that the new transformed equation does not contain x^(2) term. Then k = |
| Answer» ANSWER :D | |
| 10846. |
Determine the absolute maximum and absolute minimum values of each of the following in the stated domains : (i) y=(1)/(2)x^(2)+5x+(3)/(2),-6lexle-2 (ii) f(x)=(x+1)^(2//3), 0 le xle 8. |
|
Answer» (II) `3root3(3)` |
|
| 10847. |
What is the minimum number of moves required to move from the situation in the left to that in the right if the valid moves for bishop, rook, knight, king and pawn are shown below? is valid moved of |
|
Answer» 9  HENCE, total NUMBER of steps =18 |
|
| 10848. |
A manufure of a line f patent meducines is preparing a prodiction plan on medicines A and B. There are sufficient ingredients available to make 20000 bottes of A and 40000 bottles of B but there are only 45000 bottles int which either of the medicines can be put. Furthermore, it takes 3 horus to prepare enough material to fill 1000 bottles of B, and there are 66 hours available for this operation. The profit Rs. 8 per bottle for A and Rs.7 per bottle for B. How should the manufacturer schedule the production in order to maximize his profit? Also find the maximum profit. |
|
Answer» |
|
| 10849. |
If xy^2z < 10, then which one of the following statements must also be true? I xz < 0 II. z < 0 xyz < 0 |
|
Answer» NONE |
|
| 10850. |
If P(not B) = 0.65, P(A cup B)=0.85 and A and B are independent events, then find P(A). |
|
Answer» |
|