InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 11751. |
Find the sum of the following C_1 - 2C_2 + 3C_3 - ..... + n(-1)^(n-1) C_n |
|
Answer» SOLUTION :L.H.S. : `C_0 + 3C_1 + 5C_2 + ... + (2N+1)C_n` `sum_(k=1)^n (2K+1) C_k` = `C_0 + sum_(k=1)^n(2k+1) "^nC_k `"^nC_0 + sum(k=1)^n 2k ^nC_k + sum(k=1)^n ^nC_k `"^nC_0 + 2sum_(k=1)^n n ^(n-1)C_(k-1) + (^nC_1 + ^nC_2 + ^nC_n)` `("^nC_0 + ^nC_1 + ^nC_2 + .... + ^nC_n) + 2n^(n-1)C_0 + ^(n-1)C_1 + ... + ^(n-1)C_(n-1) ) `2^n + 2n.2(n-1)` = `2^n + n.2^n` = `(n+1)2^n` R.H.S. |
|
| 11752. |
The point of intersection of the direct common tangents drawn to the circles (x+11)^(2)+(y-2)^(2)=225 and (x-11)^(2)+(y+2)^(2)=25 is |
| Answer» Answer :D | |
| 11753. |
Find dy/dxifxy=e^((x-y)) |
| Answer» SOLUTION :`LOG(XY)=(X-y)LOGE` `logx+logy=x-y` `1/x+1/ydy/dx=1-dy/dx` `(1/y+1)dy/dx=1-1/x` `dy/dx=(1-1/x)/(1+1/y)=((x-1)/x)/((y+1)/y)="y(x-1)"/(x(y+1))` | |
| 11754. |
Statement-I : If (x^(2)+3x+1)/(x^(2)+2x+1)=A+(B)/(x+1)+(C)/((x+1)^(2)), then A+B+C=0 Statement-II: If (x^(2)+2x+3)/(x^(3))=A/x + (B)/(x^(2))+(C)/(x^(3)), then A+B-C=0 Which of the above statements is true |
|
Answer» only I is true |
|
| 11755. |
Let a gt 0, b gt 0, c gt 0. Then both the roots of the equation ax^2+ bx + c = 0 are |
|
Answer» real and negative |
|
| 11756. |
If 2x=y^(1//m)," then: "(dy)/(dx)= |
|
Answer» `m^(2)y^(2)` |
|
| 11757. |
"y is "50%" of "x%" of "x. {:("Quantity A","Quantity B"),(y,x):} |
|
Answer» |
|
| 11758. |
If x= t^(2) and y= t^(3), then (d^(2)y)/(dx^(2)) is equal to |
| Answer» Answer :B | |
| 11759. |
There are 5 like objects of first kind, 6 like objects of second kind, 4 like objects of third kind. Find the number of linear arrangements of these objects so that at least one object from like |
|
Answer» |
|
| 11760. |
Evalute the following integrals int (1)/((x -a)(x -b)(x-c))dx |
|
Answer» |
|
| 11761. |
sin12+sin48+sin54=? |
| Answer» | |
| 11762. |
Show that f(x) = |x| is not differentiableat x =0 |
|
Answer» SOLUTION :Left hand derivative at X =0 ` underset (x to 0^(-))(f (x) -f(0))/ (x -0) ` ` underset(h to 0) (f (0 -h) -f(0))/ ( 0-h-0) ` ` underset( h to 0)h/(-h)= -1 ` (ii)RIGHT hand derivative at x =0 ` underset(x to 0^(+)) lim (f(x) -f(0))/(x -0) ` `underset(h to 0) lim (f (0+h)-f(0))/ (0+h-0)` ` underset( h to 0) h / h =1` Since LHD ` ne ` RHD THe FUNCTION is not differentiable at x =0 |
|
| 11763. |
The population of a village increases continuously at the rate proportional to the number of its inhabitants present at any time. If the population of the village was 0,000 in 1999 and 25000 in the year 2004, what will be the population of the village in 2009 ? |
|
Answer» 31250 |
|
| 11764. |
A Bag I contain 3 red and 4 black balls. White bag II contains 5 red 6 black balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it was drawn from bag II. |
|
Answer» |
|
| 11765. |
The number of ways in which a team of eleven players can be selected from 22 players always including 2 of them and excluding 4 of them is |
|
Answer» `""^(16)C_(11)` |
|
| 11766. |
A staight line passing through O (0,0) intersect the curve (x-1)^2+(y-1)^2=1 at 'A' and 'B' and (x-2)^2+y^2=1 at C and D . If OA,OC , OD and OB form an A.P. , then the equation of the line is …………… . |
|
Answer» |
|
| 11767. |
If {:(f(x),=(10^x + 7^x - 14^x- 5^x)/(1-cos x),",","for"x != 0),(,=10/7, ",","for"x = 0):}, then f(x) is |
|
Answer» CONTINUOUS at X = 0 |
|
| 11768. |
The tangent at any point to the circle x^(2)+y^(2)=r^(2) meets the coordinate axes at A and B. If the lines drawn parallel to axes through A and B meet at P then locus of P is |
|
Answer» `1/(x^(2))+1/(y^(2))=1/(R^(2))` |
|
| 11769. |
For a reaction CH_(3)OCH_(3) (g) rarr CH_(4) (g)+H_(2) (g)+CO(g) at 750K, the rate constant is 3.52xx10^(-3)" min"^(-1). Starting with a pressure of 360 mm of Hg at this temperature in a closed container, how many minutes would it take for the pressure in the container to become 760 mm Hg ? (Take log 2.25 = 0.352) |
|
Answer» |
|
| 11770. |
(i) Twelve balls are distributed at random among three boxes what is the probability that the first box will contain 3 balls ? (ii) If 'n' different biscuits are distributed amoong N beggers, find the chance that a particular begger receives exactly r ( lt n) biscuits. |
|
Answer» `(ii) (.^(n)C_(R )(N-1)^(n-r))/(N^(n))` |
|
| 11771. |
If 3x+2y=3 and 2x+5y=1 are conjugate lines w.r.t the circle x^(2)+y^(2)=r^(2) then r^(2)= |
|
Answer» `3/16` |
|
| 11773. |
Ifx=h+asecthetaandy= k + b "cosec" thetathen |
|
Answer» ` (a^2 ) /((x +H)^2) - (B^2 )/((y +K)^2 ) =1` |
|
| 11774. |
If A={:[(3,2,6),(1,1,2),(2,2,5)]:},B={:[(1,2,-2),(-1,2,-2),(-,-2,1)]:}, then |
|
Answer» AB is not a SCALER matrix |
|
| 11775. |
Let f(x) = (x-3) ^(2018) (2-x)^(2019) , x in R . If (alpha) is a relative maximum of f at alpha, then 2alpha _3 f(alpha)= |
|
Answer» `(20186)/(4037)` |
|
| 11776. |
If a , b , c in Rsuch that a + b + c= 0 and az_(1) + bz_(2) + cz_(3) = 0 then z_(1) , z_(2) , z_(3) are |
|
Answer» COLLINEAR |
|
| 11777. |
If A, B, c are three square matrices such that AB=AC implies B=C, then the matrix is always a/an |
|
Answer» DIAGONAL matrix |
|
| 11778. |
Assertion(A) : The locus of the point of intersection of perpendicular tangents to y^(2)= 4ax is its directrix.Reason (R) : If theta is acute angle between the pair of tangents drawn from (x_(1),y_(2)) to parabola S =0 then tan theta= (sqrt(S_(11)))/(|x_(1)+a|) The correctanswer is |
|
Answer» Both A and R are TRUE and R is the correct EXPLANATION of A |
|
| 11780. |
Let A_(alpha)=[(cosalpha, -sinalpha,0),(sinalpha, cosalpha, 0),(0,0,1)], then : |
|
Answer» `A_(ALPHA+beta)=A_(alpha)A_(beta)` |
|
| 11781. |
If int (dx)/(x^(2) + 2x+ 2)= f(x) + c then f(x) = |
|
Answer» `TAN^(-1) ` (X+ 1) |
|
| 11782. |
Two perpendicular tangents to the ellipse (x^2)/(16)+(y^2)/(9)=1 are such that the auxiliary circle intercepts chord of length l_1" and "l_2 on these tangents, then : |
|
Answer» These TANGENTS INTERSECT on the circle `x^2+y^2=49` |
|
| 11783. |
If P (A) =6/11,P(B)=5/11and P(AnnB)=7/11,find P(A/B) |
|
Answer» <P> SOLUTION :P(B/A)=`(P(ANNB))/(P(A))`=4/11/6/11=4/5=4/6=2/3 |
|
| 11784. |
DeltaABC is an equilateral triangle. Its side is l. Any point P lies on the circum centre of DeltaABC. Then |bar(PA)|^(2)+|bar(PB)|^(2)+|bar(PC)|^(2) = ……………. |
| Answer» Answer :A | |
| 11785. |
int(2-sin 2x)/(1-cos2x)e^(x) dx is equal to |
|
Answer» `-E^(x)COT x+c` |
|
| 11786. |
int_(2)^(3)1/x dx |
|
Answer» |
|
| 11787. |
int_0^1(x^5(4-x^2))/sqrt(1-x^2)dx |
|
Answer» Solution :`int_0^1(x^5(4-x^2))/SQRT(1-x^2)DX` =`int_0^(pi/2)(sin^5theta(4-sin^2theta))/costheta.costhetad THETA` (where `x=sintheta` `rArr dx=costhetad theta`) =`4int_0^(pi/2)sin^5thetad theta-int_0^(pi/2)sin^7thetad theta` =`4 CDOT 4/5 cdot 2/3 - 6/7 cdot 4/5 cdot 2/3` =`8/15(4-6/7)=8/15cdot22/7=(176)/105` |
|
| 11788. |
Usingintegration, findthe areaoftheregionboundedby theline2y = 5x+ 7, x axisandthe linesx=2andx=8. |
|
Answer» |
|
| 11789. |
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day? |
Answer» Solution :Let the manufacturer produces `x` packets of nuts and `y` packets of bolts, then 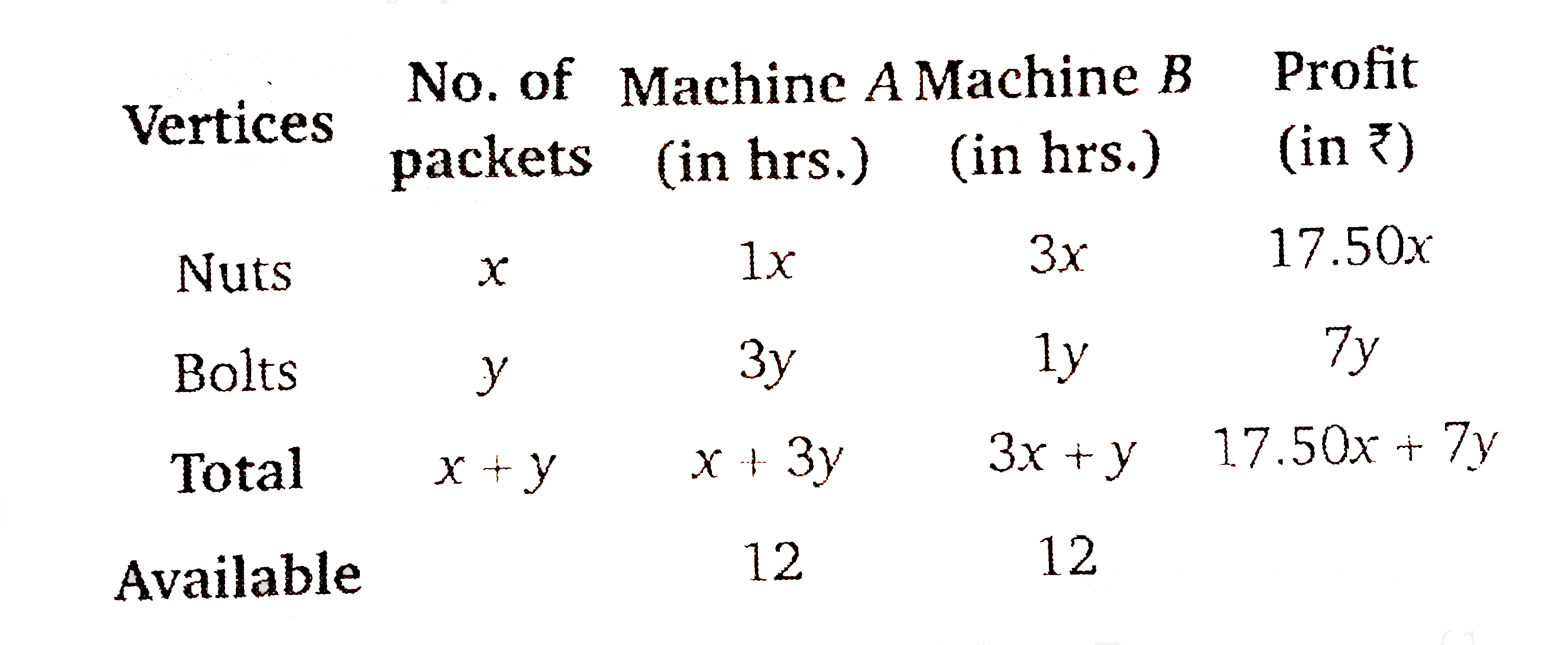 `:.` Maximise `Z=17.5x+7y`……………….1 and constraints `x+3yle12`………………………2 `3x+yle12`………………….3 `xge0,yge0`………………...4  First draw the graph of the line `x+3y=12`. 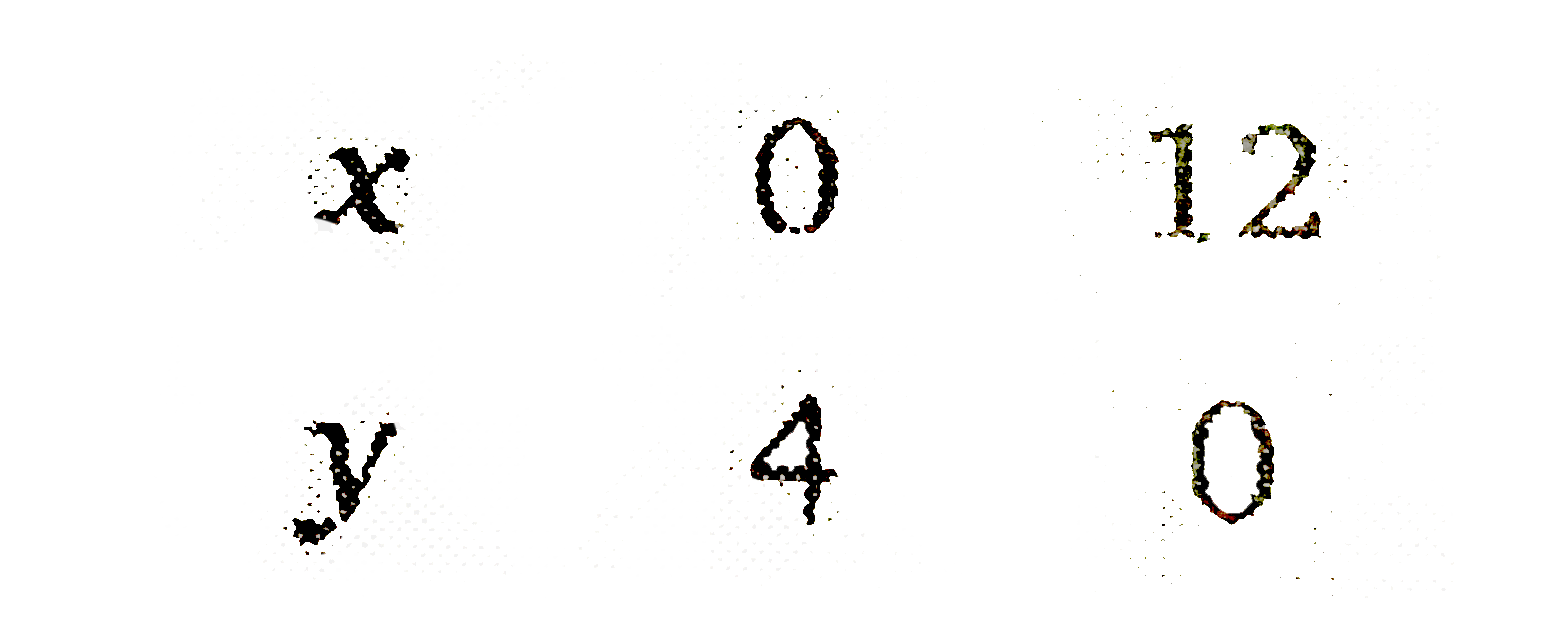 Put `(0,0)` in the inequation `x+3yge12` , `0+3xx0le10implies0le12` (True) Therefore half PLANE contains the origin. Since `x,yge0`. So the feasible region is in first quadrant, Now draw the graph of the line `3x+y=12` 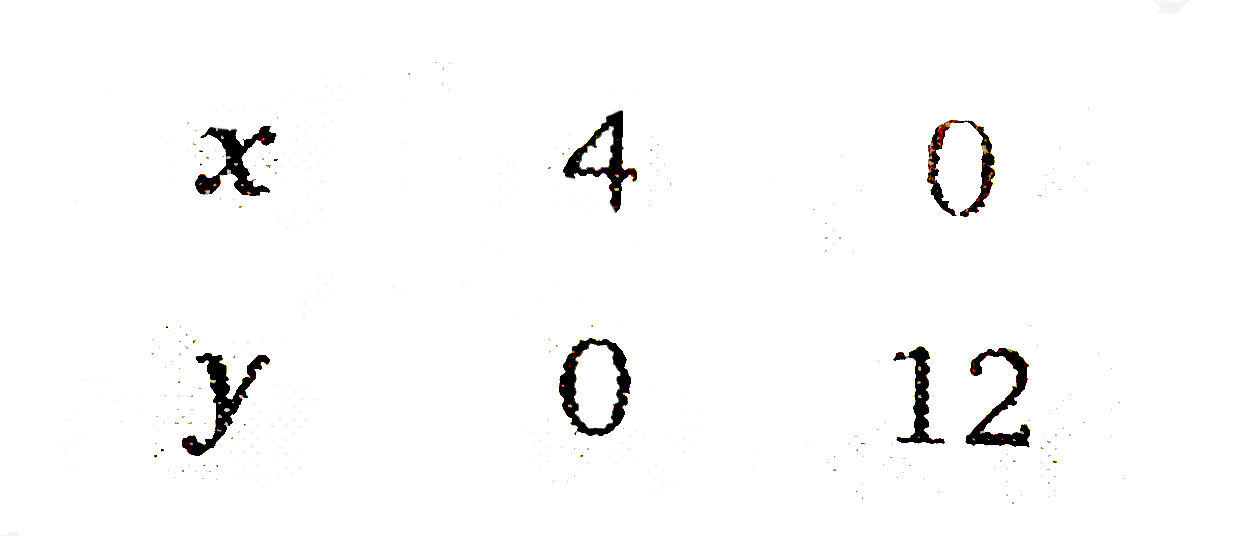 Put `(0,0)` in the inequation `3x+yle12`, `3xx0+0le12gt0le12` (True) Therefore, the half plane contains the origin. From the equations `x+3y=12` and `3x+y=12`, the point of INTERSECTION is `B(3,3)`. `:.` The feasible region is OABCO whose VERTICES are `O(0,0),A(4,0),B(3,3)` and `C(0,4)`. Now, we find the value of `Z` at these points, 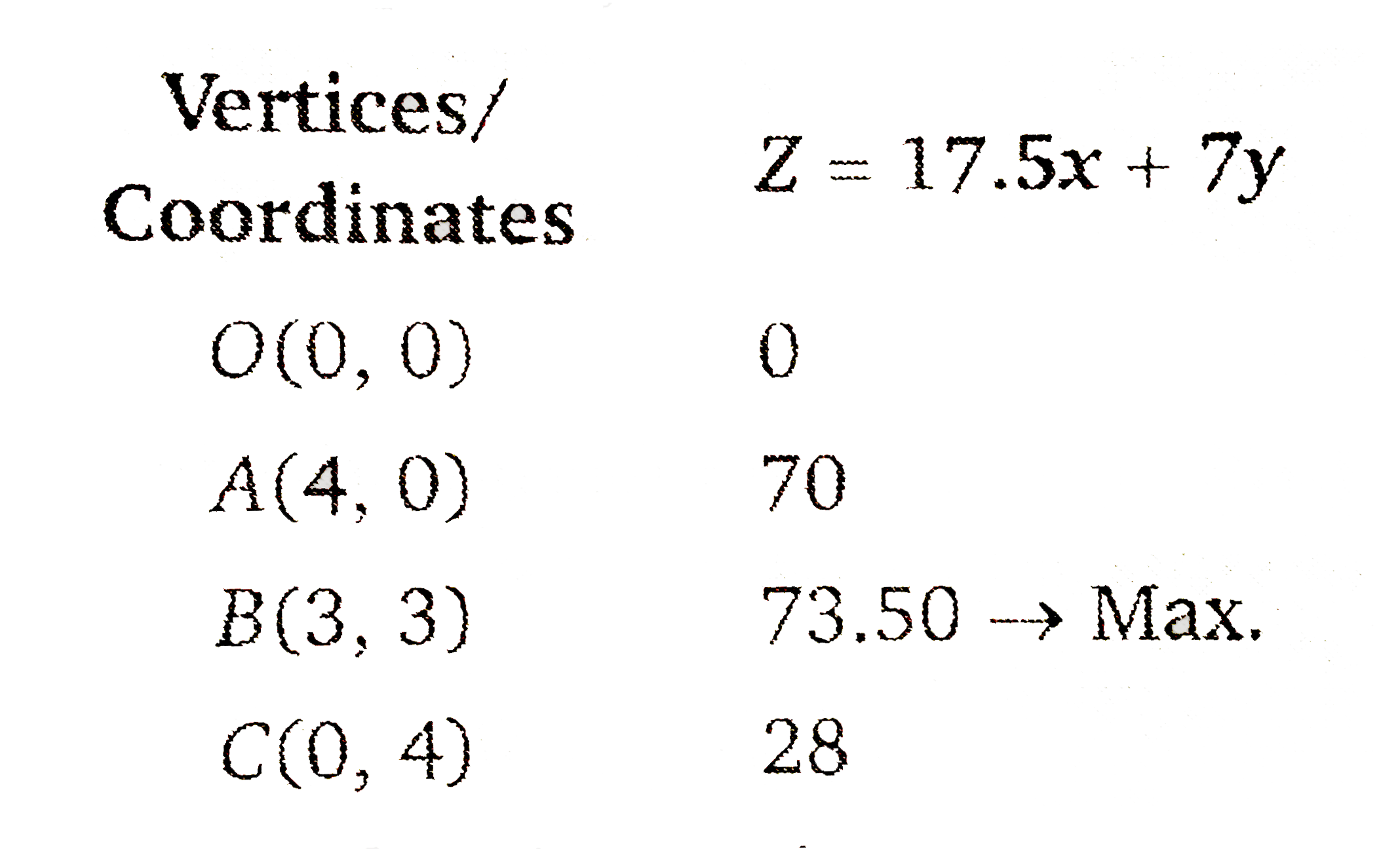 The value of `Z` is maximum Rs. 73.50 at point `(3,3)`. Therefore, the maximum profit of Rs. 73.50 can be obtained when 3 packets of nuts and 3 packets of bolts are produced PER DAY. |
|
| 11790. |
Consider the quadrationax^(2) - bx + c =0,a,b,c in N whichhas two distinct real roots belonging to theinterval (1,2). The least value of a is |
|
Answer» 4 Let `f(x) = ax^(2) - bx + c `be thecorrespoding quadratic expression and `alpha,beta` be the roots of `f(x) = 0`. 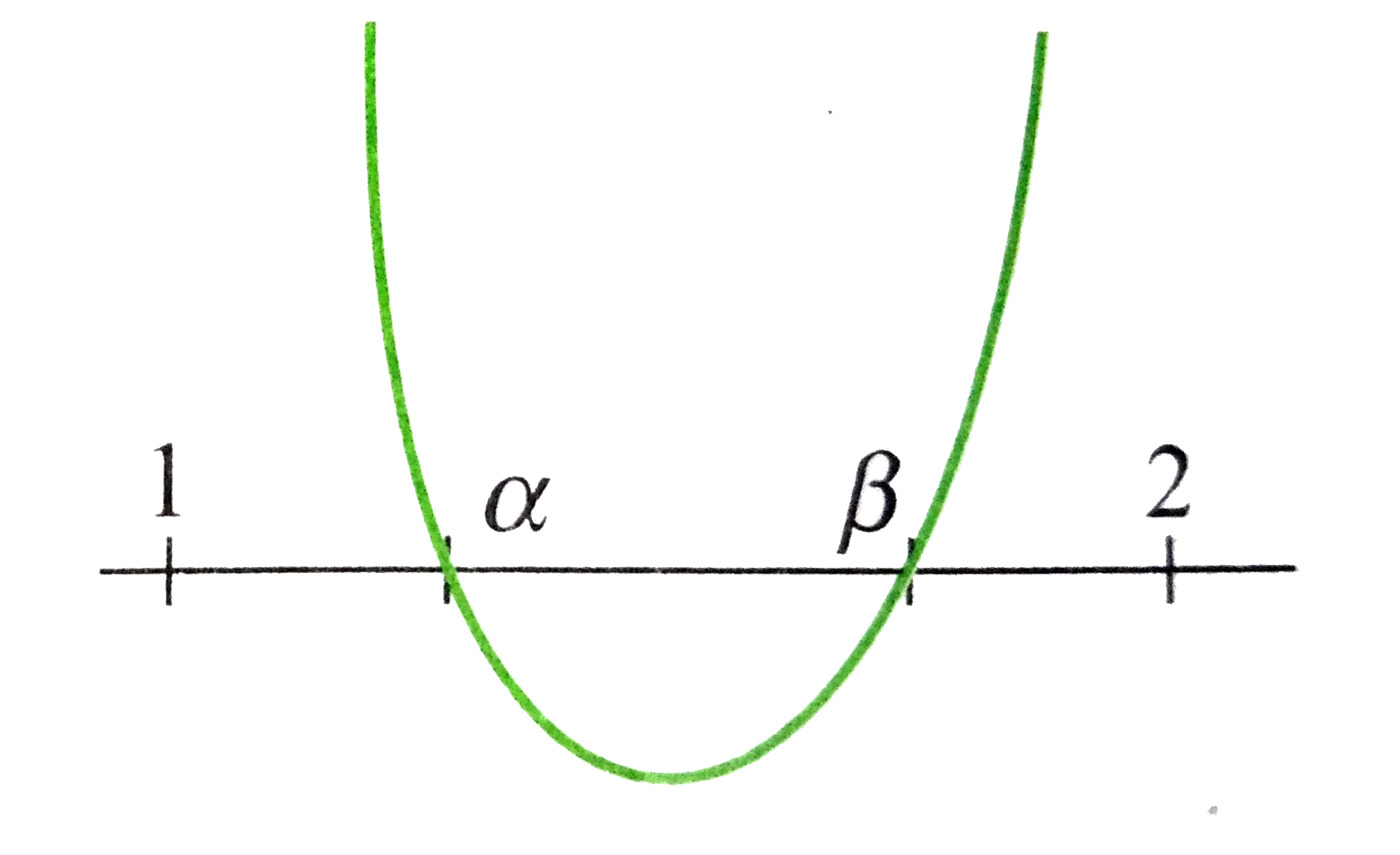 Then, `f(x) = a(x-alpha) (x -beta)` Now, `af(1) gt 0, af(2) gt 0,1lt(b)/(2a) LT2,b^(2) - 4ac gt 0` `rArr a(1-alpha) (1-beta) gt 0, a(2-alpha)(2-beta) gt 0, 2a lt b lt 4a, b^(2) - 4ax gt 0` `rArr a^(2) (1-alpha)(1-beta)(2-alpha) (2-beta) gt 0` `rArr a^(2) (1-alpha)(1-beta)(2-alpha)(2-beta) gt 0` As `f(x)` and `f(2)` both are integers and `f(1) gt 0`, and `f(2) gt 0`, so `f(1)f(2) gt 0` `rArr f(1) f(2) gt 1` `rArr 1ge a^(2)(alpha -1)(2-alpha)(beta-1)(2-beta)""(1)` Now, `((alpha-1)+(2-alpha))/(2)gt ((alpha -1)(2-alpha))^(1//2)` `rArr (alpha -1)(2-alpha) le (1)/(4)` Similarly, `(beta -1)(2-beta) le (1)/(4)` `rArr (alpha -1)(2-alpha) (beta- 1)(2-beta)lt (1)/(16)` As ` alpha ne beta`, so `alpha^(2) gt 1""("Using (1)")` `rArr a gt 5` `rArr b^(2) gt 20c and b gt 10 rArr b ge 11` Also, `b^(2) gt 100 rArr c gt 5 rArr c ge 6` |
|
| 11791. |
Consider the quadrationax^(2) - bx + c =0,a,b,c in N whichhas two distinct real roots belonging to theinterval (1,2). Theleastvalue of c is |
|
Answer» 4 Let `f(x) = ax^(2) - bx + c `be thecorrespoding quadratic EXPRESSION and `alpha,beta` be the roots of `f(x) = 0`. 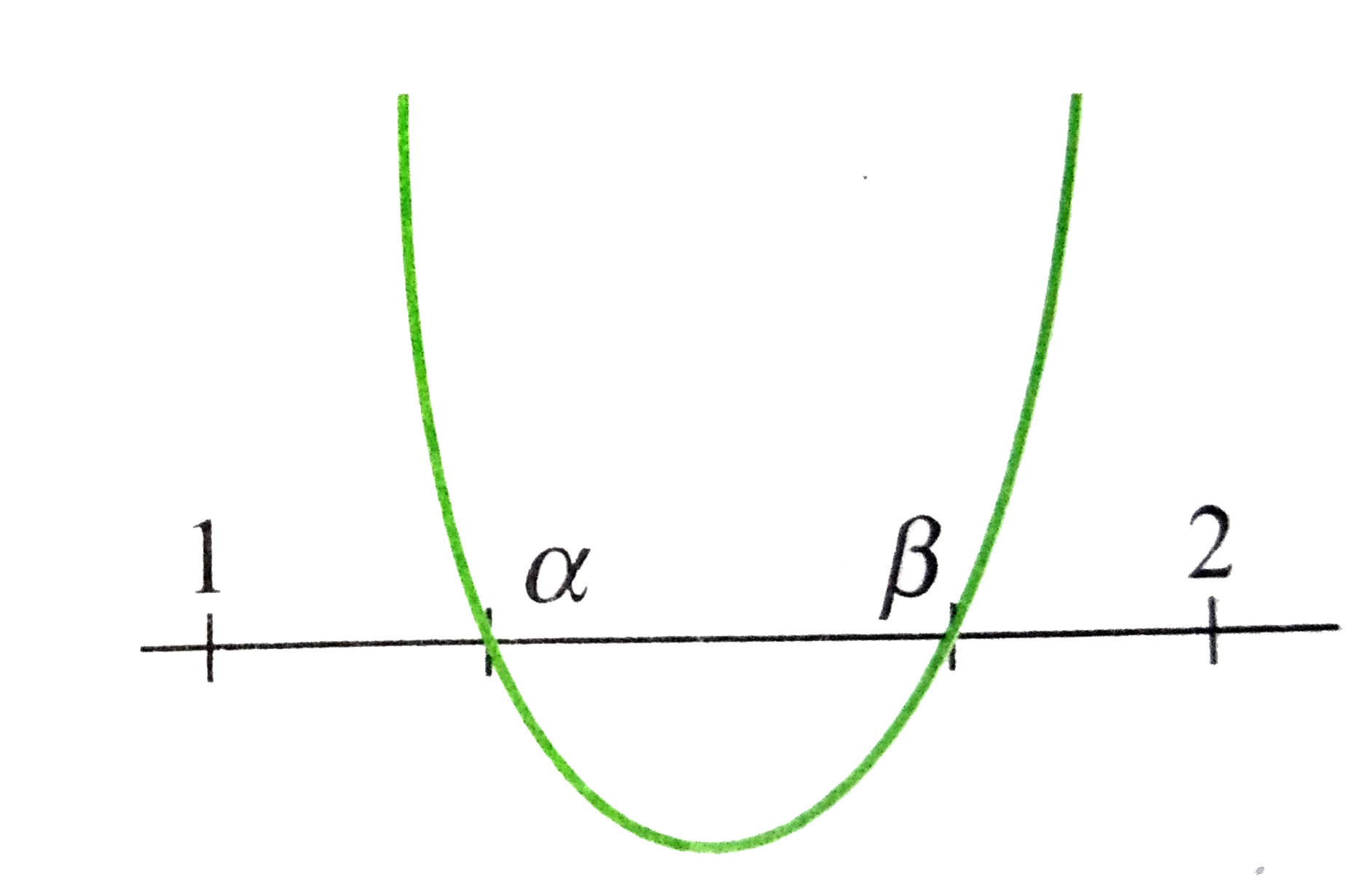 Then, `f(x) = a(x-alpha) (x -beta)` Now, `af(1) gt 0, af(2) gt 0,1lt(b)/(2A) lt2,b^(2) - 4ac gt 0` `rArr a(1-alpha) (1-beta) gt 0, a(2-alpha)(2-beta) gt 0, 2a lt b lt 4a, b^(2) - 4ax gt 0` `rArr a^(2) (1-alpha)(1-beta)(2-alpha) (2-beta) gt 0` `rArr a^(2) (1-alpha)(1-beta)(2-alpha)(2-beta) gt 0` As `f(x)` and `f(2)` both are integers and `f(1) gt 0`, and `f(2) gt 0`, so `f(1)f(2) gt 0` `rArr f(1) f(2) gt 1` `rArr 1ge a^(2)(alpha -1)(2-alpha)(beta-1)(2-beta)""(1)` Now, `((alpha-1)+(2-alpha))/(2)gt ((alpha -1)(2-alpha))^(1//2)` `rArr (alpha -1)(2-alpha) le (1)/(4)` Similarly, `(beta -1)(2-beta) le (1)/(4)` `rArr (alpha -1)(2-alpha) (beta- 1)(2-beta)lt (1)/(16)` As ` alpha ne beta`, so `alpha^(2) gt 1""("USING (1)")` `rArr a gt 5` `rArr b^(2) gt 20c and b gt 10 rArr b ge 11` Also, `b^(2) gt 100 rArr c gt 5 rArr c ge 6` |
|
| 11792. |
Consider the quadrationax^(2) - bx + c =0,a,b,c in N whichhas two distinct real roots belonging to theinterval (1,2). The least value of b is |
|
Answer» 10 Let `F(x) = ax^(2) - bx + c `be thecorrespoding quadratic expression and `alpha,beta` be the roots of `f(x) = 0`.  Then, `f(x) = a(x-alpha) (x -beta)` Now, `AF(1) gt 0, af(2) gt 0,1lt(b)/(2a) lt2,b^(2) - 4ac gt 0` `rArr a(1-alpha) (1-beta) gt 0, a(2-alpha)(2-beta) gt 0, 2a lt b lt 4a, b^(2) - 4ax gt 0` `rArr a^(2) (1-alpha)(1-beta)(2-alpha) (2-beta) gt 0` `rArr a^(2) (1-alpha)(1-beta)(2-alpha)(2-beta) gt 0` As `f(x)` and `f(2)` both are integers and `f(1) gt 0`, and `f(2) gt 0`, so `f(1)f(2) gt 0` `rArr f(1) f(2) gt 1` `rArr 1ge a^(2)(alpha -1)(2-alpha)(beta-1)(2-beta)""(1)` Now, `((alpha-1)+(2-alpha))/(2)gt ((alpha -1)(2-alpha))^(1//2)` `rArr (alpha -1)(2-alpha) le (1)/(4)` Similarly, `(beta -1)(2-beta) le (1)/(4)` `rArr (alpha -1)(2-alpha) (beta- 1)(2-beta)lt (1)/(16)` As ` alpha NE beta`, so `alpha^(2) gt 1""("Using (1)")` `rArr a gt 5` `rArr b^(2) gt 20C and b gt 10 rArr b ge 11` Also, `b^(2) gt 100 rArr c gt 5 rArr c ge 6` |
|
| 11793. |
A plane has intercepts p-1,1 and p+1 on the coordinate axes x, y and z respectively. If the distance of plane from the origin is 1//sqrt(3), then the largest value of p is: |
| Answer» ANSWER :D | |
| 11794. |
I. underset(x to 0)"Lt" (log_(e)(1+x))/(3^(x)-1)=log_(3)e II. underset(x to 1)"Lt" (log_(5) 5x)^(log_(x)5)=e |
|
Answer» only I is true |
|
| 11795. |
The standard deviation of a,a+d,a+2d,……,a+2nd is |
|
Answer» ND |
|
| 11796. |
Statement 1: Let A,B,C be the image of point P(a,b,c) in YZ,ZX andXY planes respectively. Then, the equation of the plane passing through points A,B,C cuts intercepts a,b,c on the coordinate axes.Statement 2: The image (alpha, beta, gamma) of a point (x_(1),y_(1),z_(1)) in the plane ax+by+cz+d=0 is given by(alpha-x_(1))/a=(beta-y_(1))/b=(gamma-z_(1))/c=-(2(ax_(1)+by_(1)+cz_(1)+d))/(a^(2)+b^(2)+c^(2)) |
|
Answer» STATEMENT-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1. Using statement 2 the image of POINT `P(a,b,c)` in `yz,zx` and `xy` planes are `A(-a,b,c),B(a,-b,c)` and `C(a,b,-c)` respectively. LET the equation of the plane passing through `(a-,b,c)` be `U(x+a)+V(y-b)+W(z-c)=0`..............i It passes through `(a,-b,c)` and `(a,b,-c)` `:. 2Ua-2Vb=0W=0` `2Ua+0V-2Wc=0` `impliesU/(4bc)=V/(4ac)=W/(4ab)` Substituting the values `U,V,W ` in (i)we OBTAIN `bc(x+a)+ca(y-b)+ab(z-c)=0impliesx/a+y/b+z/c=1` Clearly, this plane cuts intercepts a,b and c on the coordinate axes. |
|
| 11797. |
If 3^(rd), 7^(th) and 12^(th) terms of A.P. are three consecutive terms of a G.P., then the common ratio of G.P is |
|
Answer» `5/4` |
|
| 11799. |
{{:(-x^(2)+4x+a","xle3,),(ax+b","3ltxlt4,),(-(b)/(4)x+6","xge4,):}If x=3 isa point of minima and x=4 is a point of mxima then which of the following is true? |
|
Answer» `alt0,BGT0` |
|
| 11800. |
Show that the coefficient of a^m and a^n in expansion of (1+a)^(m+n) are equal. |
|
Answer» SOLUTION :(m+1)TH and (n+1)th TERM in the expansion of `(1+a)^(m+n)` are `"^(m+n)C_m a^m` and `^(m+n)C_n a^n` `THEREFORE` The coefficient of `a^m` and `a^n` are `"^(m+n)C_m` and `^(m+n)C_n` which are EQUAL. |
|