InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3001. |
Assertion (A) : X is a binomial distribution with parameters n = 100 and p . If P (x = 50) = P ( x = 49) then p = (1)/(2) Reason (R) : For the binomial distribution (q + p)^n , P (x = k) = ""^(n) c_(k) .q^(n-k) .p^(k) |
|
Answer» A is false , R is true |
|
| 3002. |
Find the volume of the solid of revolution when the region bounded by y=sqrt(x), y=2 and x=0 is rotated about the x axis . |
|
Answer» `(16pi)/(5)` |
|
| 3003. |
A: The plane 2x + 3y + 5 = 0 is parallel to x-axis. R: The plane ax + by + cz +d=0 is parallel to x-axis if a = 0. |
|
Answer» both A and R are TRUE and R is the correct explanation of A |
|
| 3004. |
Let z be a purely imaginary number such that Im (z) < 0. Then arg (z) is equal to |
| Answer» ANSWER :D | |
| 3005. |
A certain mass of an ideal gas is expanded from (1L, 10 bar) to (4L,5bar) against a constant external pressure of 1 bar. If initial temperature of gas is 300 K and the heat capacity of process is 50J//""^(@)C. Then the enthalpy change during the process is : |
|
Answer» `DeltaH=14.7 KJ` `(P_(1)V_(1))/(T_(1))=(P_(2)V_(2))/(T_(2))implies(10xx1)/(300)=(5xx4)/(T_(2))` `implies T_(2)=600K` `Q=CDeltaT=50xx[600-300]=15000` Joule=15kJ `W=-P_("EXT")[V_(2)-V_(1)]` `=-1[4L-1L]=-`3BAR litre=-0.3 kJ `Delta=Q+W` `=15-0.3=14.7kJ` `Delta=DeltaU+(P_(2)V_(2)-P_(1)V_(1))` `=[14.7+(5xx4-10xx1)/(10)]kJ=15.7` |
|
| 3006. |
There are factories located one at place P and other at place Q from which a certin commodity is to be delivered to each of three depot situated at A,B and C. The weekly requirement of the depots are respectively 5,5 and 4 units of the commodity while the production capacity of the factories P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below. How many units should be transported from each factory to each depot in order that the transportation cost is minimum. Also find the minimum transportation cost. |
|
Answer» <P> Solution :Let `x` and `y` units of commodity be TRANSPORTED from the factory `P` to depots A and B respectively. Thus `(8-x-y)` units will be transported from `P` to depot `C`.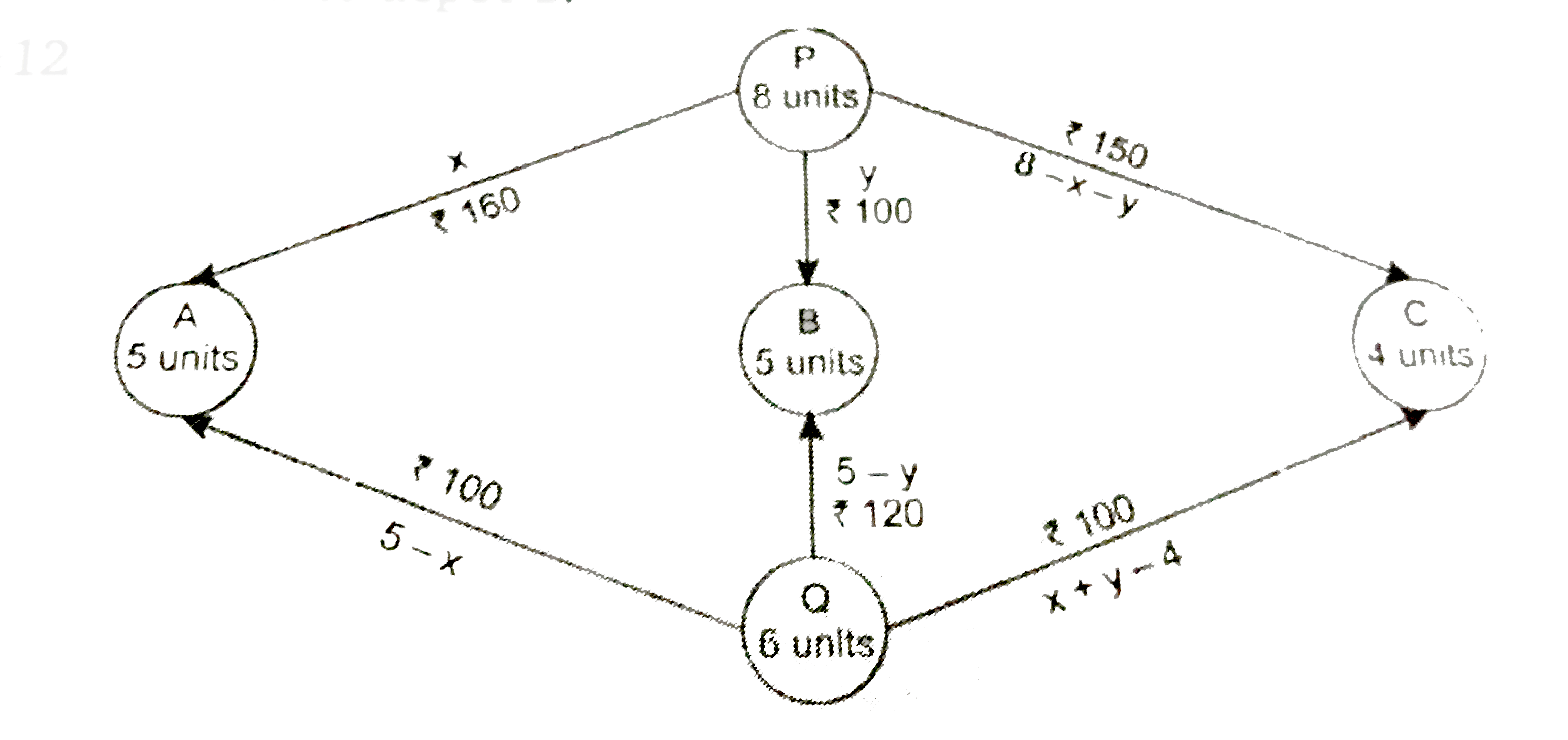 Now the number of units transported from `Q` factory to the depots A,B and C will be `5-x,5-y` and `x+y-4` respectively as shown in the diagram. Therefore `xge0` `yge0` `8-x-yge0impliesx+yle8` `5-xge0impliesxle5` `5-tge0impliesyle5` `x+y-4ge0impliesx+yge4` and transportation cost `z=160x+100y+150(8-x-y)+100(5-x)` `+120(5-y)+100(x+y-4)` `=160x+100y+1200-150x-150y+500` `-100x+600-120y+100x+100y-400` `=10x-70y+1900` Thus the linear PROGRAMMING problem is Minimize `z=10x-70y+1900` Subject to: `xge0` `yge0` `XLE5` `yle5` `x+yle8` `x+yge4` Draw the graph of corresponding equations and obtain the feasible region and SHADE it. The convex region is ABCDEF whose vertices are `A(4,0),B(5,0),C(5,3),D(3,5),E(0,5)` and `F(0,4)`. We will find the value of `z` at each of these vertices. 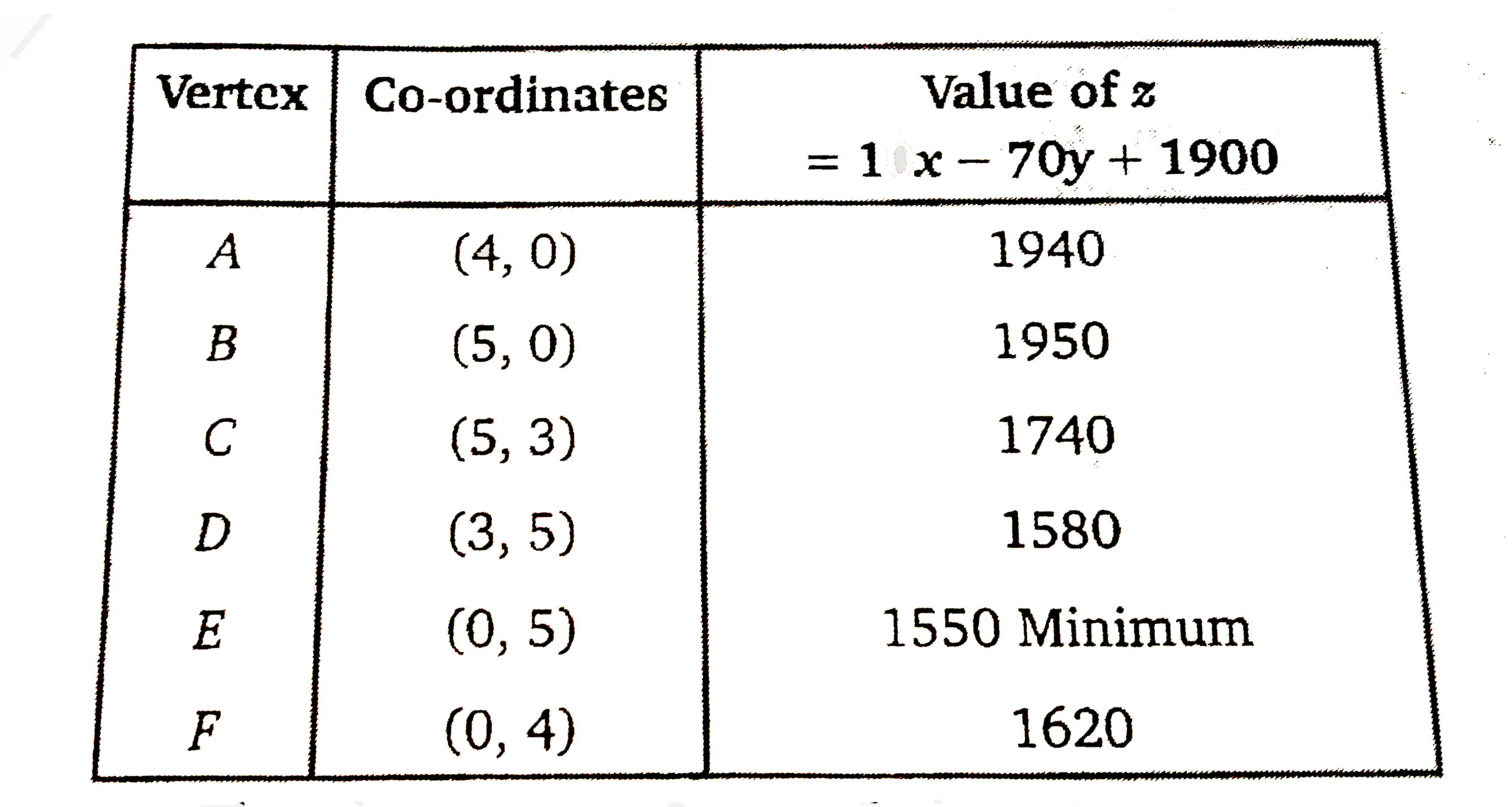 Therefore at `x=0,y=5` the minimum cost is Rs. 1551. 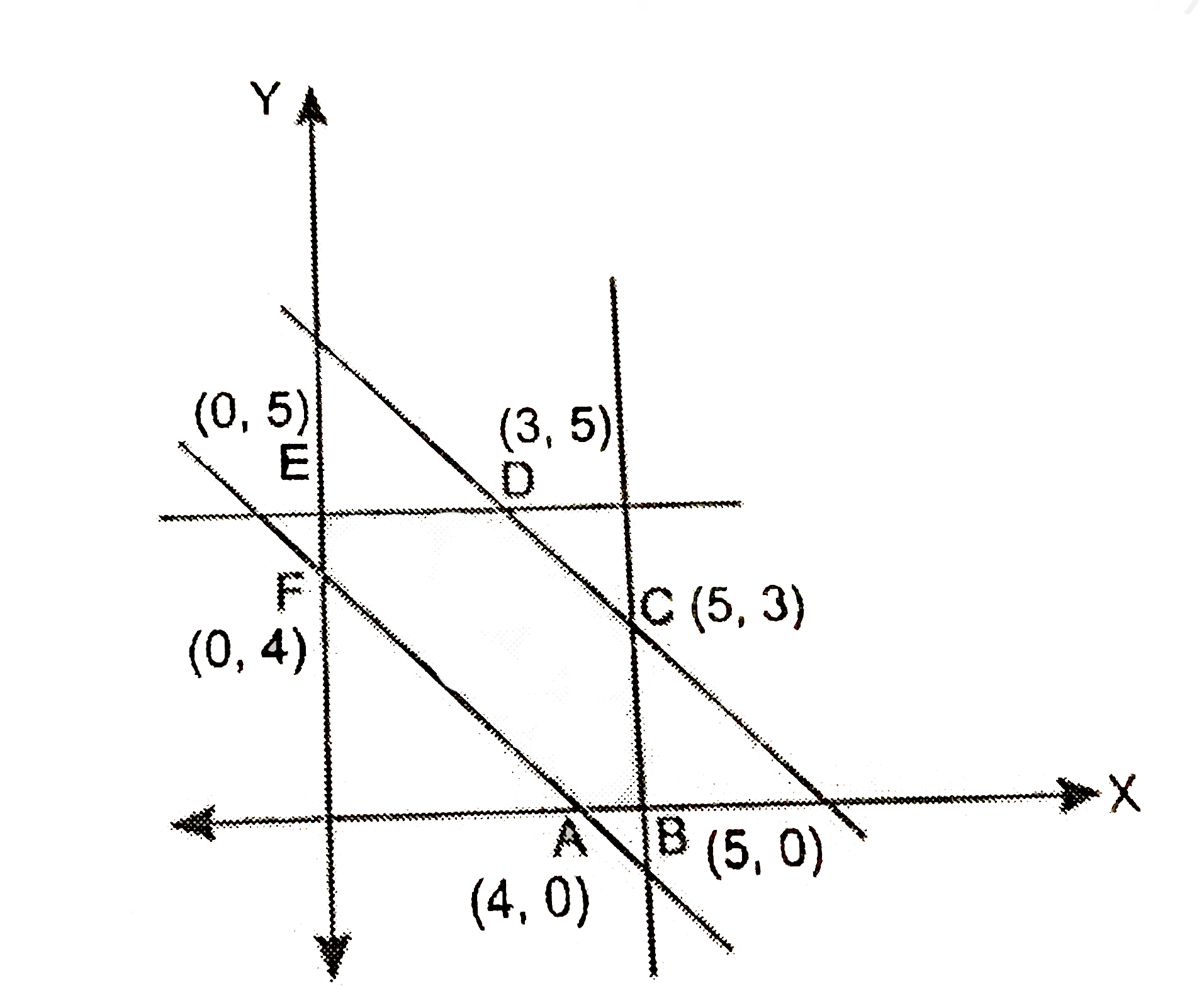 Therefore for minimum cost of transportation we will transport 0,5 and 3 units from `P` to A,B and Crespectively and 5,0 and 1 unit from `Q` to A,B and C respectively. |
|
| 3007. |
If int f(x)dx=f(x), then int[f(x)]^(2)dx=... |
|
Answer» `(1)/(2)[f(X)]^(2)` |
|
| 3008. |
Show that straight line 7x+6y=13 is a tangent to the parabola y^(2)-7x-8y+14=0 and find the point of contact. |
|
Answer» |
|
| 3009. |
If R(t)=[(cost,si nt),(-si nt,cost)], then R(s)R(t) equals |
| Answer» Answer :A | |
| 3010. |
For each binary operation ** defined below, determine whether ** is commutative or associative on Z, define a**b=a-b |
|
Answer» SOLUTION :Since `1-2ne2-1, 1**2 ne 2**1` `therefore ** ` is not COMMUTATIVE Since `(2-4)-5ne2-(4-5), `(2**4)**5 ne 2**(4**5)` `therefore **` is not associative |
|
| 3011. |
int (1)/(x^(2)(x^(4)+1)^(3//4))dx is equal to___________ |
|
Answer» `(-(1+x^(4))^(3//4))/(x)+C` |
|
| 3012. |
The solution of the equation int_(0)^(x) (1)/(xsqrt(2^(2)-1))dx=(pi)/(12), is |
|
Answer» x=3 |
|
| 3014. |
Sum of infinite number of terms in GP is 20 and sum of their square is 100. The common ratio of GP is |
|
Answer» 5 |
|
| 3015. |
For each of 3 years , the table below gives the number of different routes a runner ran , the number of runs she ran , and the total number of miles she ran . To the nearest tenth of a mile , what is the average number of miles the runner ran per run in 2005 ? |
|
Answer» 2.5 |
|
| 3016. |
Let o lt p lt q and a ne 0 such that the equation px^(2) +4 lambda xy +qy^(2) +4a (x+y +1) = 0 represents a pair of straight lines, then a can lie in the interval |
|
Answer» `(-oo,oo)` `p.q.4A +2.2a.2a.2lambda -p.4a^(2) -q.4a^(2)-4a.4lambda^(2) =0` `rArr 4 lambda^(2) -4a lambda + {(p+q)q-pq} =0 ( :' q ne 0)` Since, `lambda in R, 16a^(2) - 4.4 {(p+q)a-pq} ge 0` or `(a-p)(a-p) ge 0` `:. a le p` or `a ge q` |
|
| 3017. |
Using elementary row transformations , find the inverse of [{:(1,3,-2),(-3,0,-5),(2,5,0):}] |
|
Answer» |
|
| 3018. |
The number of ways of arranging the letters of the word 'SUCCESSFUL' so that Two C's are together but no two S's are together is |
|
Answer» `(7!)/(2! 2!)` |
|
| 3019. |
The vector equation of line passing through origin and parallel to (x-2)/(3)=(y-3)/(-1)=(z+1)/(2) is |
|
Answer» `barr=2hati+3hatj-hatk` |
|
| 3020. |
Construct a 2xx3 matrix having element:a_(ij)=i+j |
|
Answer» SOLUTION :`a_ji=i+ij` `"The"2XX3 "MATRIX is"` `[[a_11,a_12,a_13],[a_21,a_22,a_23]]=[[2,3,4],[3,4,5]]` |
|
| 3021. |
Construct a 2xx3 matrix having element:a_(ij)=i-j |
|
Answer» Solution :`a_ji=i+ij` `"The"2xx3 "matrix is"` `[[1-1,1-2,1-3],[2-1,2-2,2-3]]=[[0,-1,-2],[1,0,-1]]` |
|
| 3022. |
Construct a 3 xx 4 matrix, elements are given by a_(ij) = |-3i + 4j|. |
| Answer» | |
| 3023. |
For real x, the equation |x/(x-1)|+|x|=x^2/(|x-1|) has |
|
Answer» one solution |
|
| 3024. |
Findproduct: [[1,2],[3,4]][[1,0],[0,1]] |
|
Answer» SOLUTION :`[[1,2],[3,4]][[1,0],[0,1]]` `=[[1.1+2.0""1.0+2.1],[3.1+4.0" "3.0+4.1]]=[[1,2],[3,4]]` |
|
| 3025. |
Consider the areas of the four triangles obtained by drawing the diagonals AC and BD of a trapezium ABCD. The product of these areas, taken two at time, are computed. If among the six products so obtained, two product are 1296 and 576, determine the square root of the maximum possible area ofthe trapezium to the nearest integer. |
|
Answer» |
|
| 3026. |
If A, G, H denote respectively the AM, GM and HM between two unequal positive numbers, then |
|
Answer» `A = G^(2)H` |
|
| 3027. |
Number of positive integral values of N such that characteristic of N with base 'a', is 'c' are (a,cin N) :- |
|
Answer» `a^(c-1)-a^(c-2)` |
|
| 3029. |
Consider f(x)=int_(-1)^(x)(e^((x-t)/(x-2-t))dt)/(x-2-t)^(2) Q. The greatest integer in range of f(x) is |
|
Answer» 0 `IMPLIES(1)/((x-2-t)^(2))dt=du` `f(x)=int_((1)/(x-1))^(-(1)/(2))e.e^(2u)du` `f(x)=(e)/(2).(e^(-1)-e^((2)/(x-1)))` `f(x)=(1)/(2)-(e)/(2).e^((2)/(x-1))` (1) `f(x)LT(1)/(2)` for all `xepsilonR` `implies` Greatest integer in the Range `=0` (2) `f^(')(x)=(e)/((x-1)^(2))e^((2)/(x-1))` `f^(')(-1)=(1)/(4)(x+1)` `impliesy` INTERCEPT`=(1)/(4)` |
|
| 3030. |
Integrate the following functions x sin 3x |
|
Answer» Solution :`INT X SIN 3x dx` =`x(-COS(3x)/3) - int 1xx cos(3x)/3 dx` =`-(x cos 3x)/3 + 1/3 ((sin(3x)/3) +c` =`-1/3 x cos 3x +1/9 sin 3x +c` |
|
| 3031. |
For n in N, int_(0)^(2pi) (x sin^(2n)x)/(sin^(2n) x + cos^(2n) x) dx= |
|
Answer» `PI` |
|
| 3032. |
int (3x + 3)/(sqrt(x^(2) + 2x +5))dx = |
|
Answer» `SQRT(X^(2) + 2X + 5) + sinh^(-1) ((x - 1)/(2)) + C` |
|
| 3033. |
If z = 3 + 3i then, z^(2)+z+15 = |
|
Answer» |
|
| 3034. |
Compute the value of 'c' satisfied by the Rolle's theorem for the function . f(x) =x^(2)(1-x)^(2), x in [0,1]. |
|
Answer» |
|
| 3035. |
Let f : N rarr R be the function defined by f(x) = (2x-1)/(2) and g : Q rarr R be another function defined by g(x) = x + 2. Then (gof) ((3)/(2)) is |
| Answer» Answer :D | |
| 3036. |
int_(pi/6)^(pi/4) " cosec "x dx |
|
Answer» Solution :`I= int_(pi//6)^(pi//4) " cosec "x dx` `=[LOG |"cosec"x-COT x|]_(pi//6)^(pi//4)` `=log |"cosec ".(pi)/(4)-cot .(pi)/(6)|` `=log |sqrt(2)-1|-log |2-sqrt(3)|` `=log |(sqrt(2)-1)/(2-sqrt(3))|` |
|
| 3037. |
If a is an integer and a in (-5,30] then the probability that the graph of the function y=x^(2)+2(a+4)x-5a+64 is strictly above the x-axis is |
|
Answer» `(1)/(5)` |
|
| 3038. |
Evaluation of definite integrals by subsitiution and properties of its : int_(0)^(4028)(f(x))/(f(x)+f(4028-x))dx=.............. |
|
Answer» 4028 |
|
| 3039. |
Let a,b,cberealnumbersa ne 0ifalphais a rootsofa^2x^2+ bx+c=0 , betais a rootsofa^2 x^2 -bx-c=0and 0 ltalpha lt beta, thenthe equationa^2 x^2 + 2bx+ 2c=0has a rootgamma hasa root gammathatalwayssatisfies |
|
Answer» `GAMMA= ( ALPHA+ BETA )//2` |
|
| 3040. |
IF 0< a |
|
Answer» REALAND distinctrootsoutof WHICHONE liesbetweenc and d |
|
| 3041. |
IF ina DeltaABC, thealtitudesfromthe verticesA,B,Con oppositesidesare inH.P ,thensin A , sin B, sin Care in |
|
Answer» H.P |
|
| 3042. |
If S -= x^(2) +y^(2) -2x =0, S' -= x^(2) +y^(2) +3x =0and if overset -( AB )is a direct common tangent to the two circles (A, B are the point of contcact ) then overset- (AB)subtends at origin an angle. |
| Answer» Answer :D | |
| 3043. |
Find the number of 4-letter words that can be formed using the letters of the word "ARTICLE which do not contain E |
|
Answer» |
|
| 3044. |
Let A(z_(1)), B(z_(2)), C(z_(3) and D(z_(4)) be the vertices of a trepezium in an Argand plane such that AB||CD Let |z_(1)-z_(2)|=4, |z_(3),z_(4)|=10 and the diagonals AC and BD intersects at P. It is given that Arg((z_(4)-z_(2))/(z_(3)-z_(1)))=(pi)/2 and Arg((z_(3)-z_(2))/(z_(4)-z_(1)))=(pi)/4 Which of the following option(s) is/are correct? |
|
Answer» Area of trepezium `ABCD` is equla to `140/3` sq. units `BP=2Y` then `CP=5x, DP=5y` Area of trapezium `ABCD=49/2xy` `tan alpha=(2x)/(5y), tan BETA =(2y)/(2x)` also `alpha+beta=45^(@)` `impliesxy=10/21(x^(2)+y^(2))` Also `AB^(2)=AP^(2)+BP^(2)impliesx^(2)+y^(2)=4impliesxy=40/21` `Ar(DeltaPCD)=5xy` 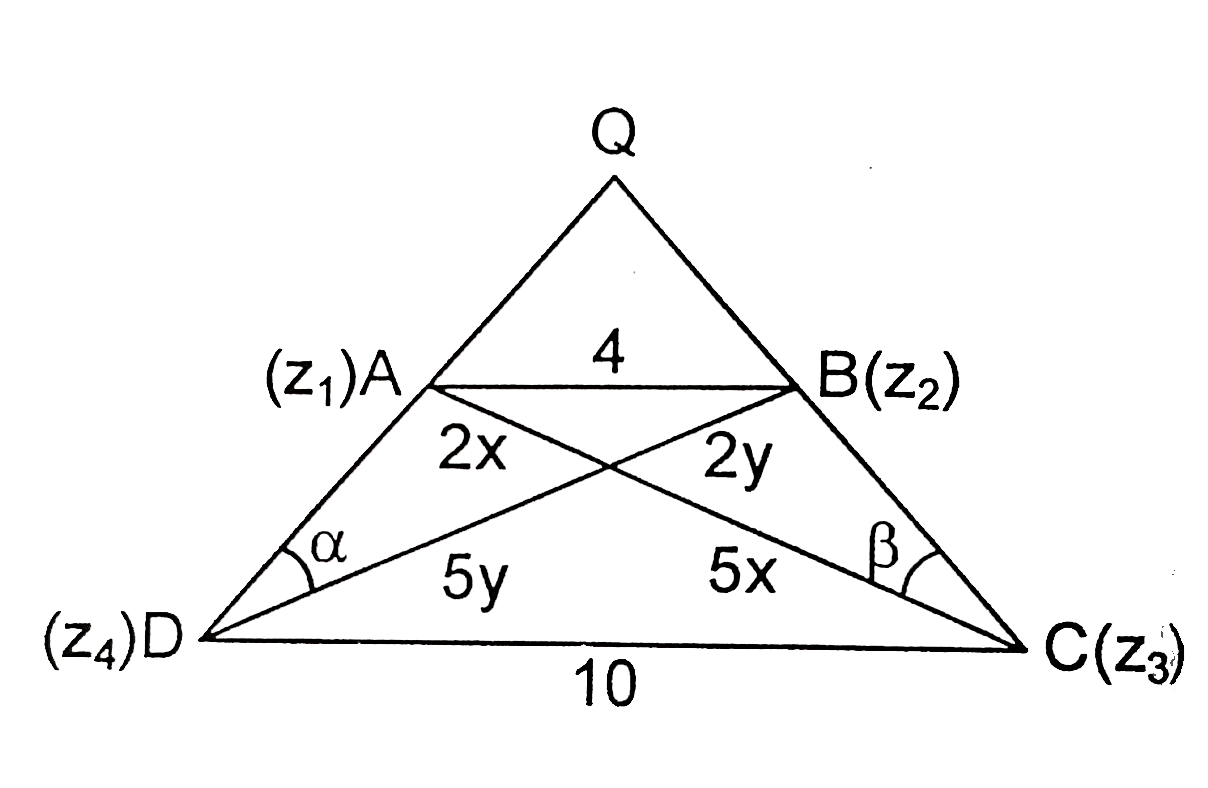
|
|
| 3045. |
Let A(z_(1)), B(z_(2)), C(z_(3) and D(z_(4)) be the vertices of a trepezium in an Argand plane such that AB||CD Let |z_(1)-z_(2)|=4, |z_(3),z_(4)|=10 and the diagonals AC and BD intersects at P. It is given that Arg((z_(4)-z_(2))/(z_(3)-z_(1)))=(pi)/2 and Arg((z_(3)-z_(2))/(z_(4)-z_(1)))=(pi)/4 Which of the following option(s) is/are incorrect? |
|
Answer» Value of `|CP-DP|` is equal to `10/(sqrt(21))` `BP=2Y` then `CP=5x, DP=5y` AREA of trapezium `ABCD=49/2xy` `TAN alpha=(2x)/(5y), tan beta =(2y)/(2x)` also `alpha+beta=45^(@)` `impliesxy=10/21(x^(2)+y^(2))` Also `AB^(2)=AP^(2)+BP^(2)impliesx^(2)+y^(2)=4impliesxy=40/21` `Ar(DeltaPCD)=5xy` 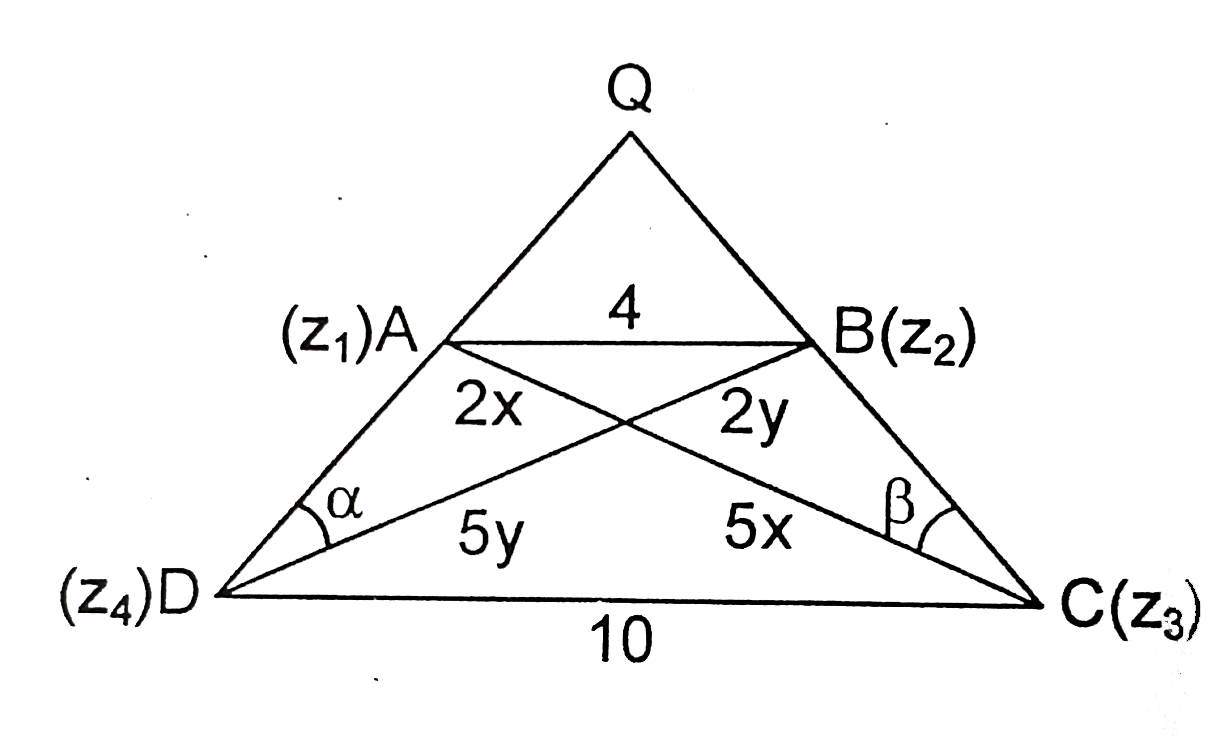
|
|
| 3046. |
"Let "F(x) =(f(x))^(2) +(f'(x))^(2),F(0)=7 where f(x) is thrice differentiable fucntion such that |f(x)|le1AAx in [-1,1]then prove the following . (i) there isatleast one point in each of the intervals (-1,-0) and (0,1) where |f'(x)|le2) (ii) there isatleast one point in eachof theintervals (-1,0) and (0,1) where F(x) le 5 (iii) there exits atleast one maxima ofF(x) " in "(-1,1) (iv) for somec in (-1,1) F(c )ge 7, F'(c )=0 " and "F''(c )le0 |
| Answer» | |
| 3047. |
Three dice are rolled 4 times . The probability of getting sum 17 exactly 3 times is |
| Answer» Answer :A | |
| 3048. |
If the equation ax^2+2hxy+by^2=0 represents a pair of lines then prove that the equation of the pair of angular bisection is h(x^2-y^2)=(a-b)xy=0. |
|
Answer» |
|
| 3049. |
Prove that for any two statements p and q the statements ~(pharr~q)andpharrq are equivalent. |
|
Answer» |
|
| 3050. |
A bomb of mass 9kg initially at rest explodes into two piece of masses 3 kg and 6 kg. The kinetic energy of the 3 kg mass is 216 J. The kinetic energy of the 6kg mass will be :- |
|
Answer» <P> `p^(2) = 2m_(2)k_(2)` `implies m_(1)k_(1) = m_(2)k_(2)` `k_(2) = (m_(1)k_(1))/(m_(2))` `k_(2) = (3xx21.6)/(9) = 108 J`. |
|