InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3051. |
If for the matrix A=[(costheta, 2sintheta),(sintheta,costheta)],A^(-1)=A^(T)then number of possible value(s) of theta in [0, 2pi] is : |
|
Answer» 2 |
|
| 3052. |
If three positive real numbers a, b, c are in A.P and abc = 4, then the minimum possible value of b is |
|
Answer» `2^(3/2)` |
|
| 3053. |
If a, b, c are positive integers such that a^2+ 2b^2-2ab = 169 and 2bc - c^2= 169 then a + b + c is: |
|
Answer» |
|
| 3054. |
Find the probability of getting 5 exactly twice in 7 throws of a die. |
|
Answer» |
|
| 3055. |
Let z_(1) = 2 + 3i and z_(2) = 3 + 4i be two points on the complex plane. Then the set of complex numbers z satisfying abs(z - z_(1))^(2) + (z - z_(2))^(2) = (z_(1) - z_(2))^(2) represents |
|
Answer» a straight line |
|
| 3056. |
If y=(tan^(-1)x)^(2), show that (x^(2)+1)^(2)y_(2)+2x(x^(2)+1)y_(1)=2. |
|
Answer» |
|
| 3057. |
if y=sec(tan^(-1)x), then (dy)/dx is equal to |
|
Answer» `X/(1+x^2)` |
|
| 3058. |
If alpha, beta , gamma are the roots of x^(3) + 3px^(2) + 3px + r = 0then the equation whose roots are alpha - (1)/( beta gamma ) , beta - (1)/(gamma alpha), gamma - (1)/(alpha beta)is |
|
Answer» `y^(3) - 29Y^(2) - 50Y + 625 = 0 ` |
|
| 3060. |
STATEMENT-1 : From point (4, 0) three different normals can be drawn to the parabola y^(2) =4x. and STATEMENT-2 : From any point, atmost three different normals can be drawn to a hyperbola. |
|
Answer» STATEMENT-1 is true, statement-2 is true, Statement -2 is a correct explanation for Statement -1 |
|
| 3061. |
(a) Find all rational values of x at which y=sqrt(x^(2)+x+3) is a rational number. (b) Prove that sqrt2 is an irrational number. |
|
Answer» |
|
| 3062. |
Method of integration by parts : I_(1)=int sin^(-1)x dx and I_(2)= int sin^(-1) sqrt(1-x^(2))dx then..... |
|
Answer» `I_(1)=I_(2)` |
|
| 3063. |
The set of all real values of x for which f(x)=log_(e)sqrt((1+x)/(1-x))+log_(e)((1+sqrt(1-x^(2)))/x)+coth^(-1)x+log_(e)((1+sqrt(1+x^(2)))/x)+sinh^(-1)x is defined is |
| Answer» ANSWER :B | |
| 3064. |
A man is known to speak the truth on an average 3 out of 4 times. He throws a fair die and reports that it is a six. The probabilitythe itis actually a six is |
|
Answer» `(3)/(5)` |
|
| 3065. |
If u_(1) = ax + by + c, u_(2) = a'x + b'y + d, u_(3) = ax + by + c', u_(4) = a'x + b'y +d' then u_(1)= 0, u_(2) = 0, u_(3) = 0, u_(4) = 0 from a parallelogram. Then the diagonal. |
|
Answer» BD can be GIVEN by `u_(2)u_(3) - u_(1)u_(4) = 0` |
|
| 3066. |
Solve (3x-4)/(2) ge (x+1)/(4) -1. Show the graph of the solutions on number line. |
|
Answer» |
|
| 3067. |
Showthat thefunction f : R to R : f (x) = {[-1 \ if \ x \ is \ irrational ], [1 \ if \ x \ is \ rational ]} ismany-oneinto. Find(i) f ((1)/(2)) \ (ii)f (sqrt(2))\ (iii) f (pi) \ (iv)f (2 +sqrt(3)) |
|
Answer» |
|
| 3068. |
Integrate the following functions 1/(sqrt(1+4x^2) |
|
Answer» SOLUTION :`int1/sqrt(1+4x^2) DX = INT 1/sqrt(1+(2x)^2) dx` =`1/2log|2x+sqrt(1+(2x)^2) dx` `1/2 log|2x+sqrt(1+4x^2)|+c` |
|
| 3069. |
P(A' cup B') | C = ……………… |
|
Answer» `1- P(A CAP B) | C ` |
|
| 3070. |
Equations of the line passing through (1,1,1) and perpendicular to the plane 2x+3y+z+5=0 are |
|
Answer» `(x+1)/( 1) = (y-1)/(3) = (z-1)/(2)` |
|
| 3071. |
Let a* b =1cm (a,b) for all values of a,b in N (i) Find (12*16) (ii) Show that* is commutative on N (iii) Find the identity element in N (iv) Find all invertible elements in N |
|
Answer» (ii)a*B=1cm (a,b) =1cm (b,a)=b*a (iii) let e be the identity element in N (iv) Let a in N be an ARBITRARY element Then `a*b=1 rarr 1cm (a,b)=1 rarr a=b=1` `therefore` 1 is the only element in N which is ivertible 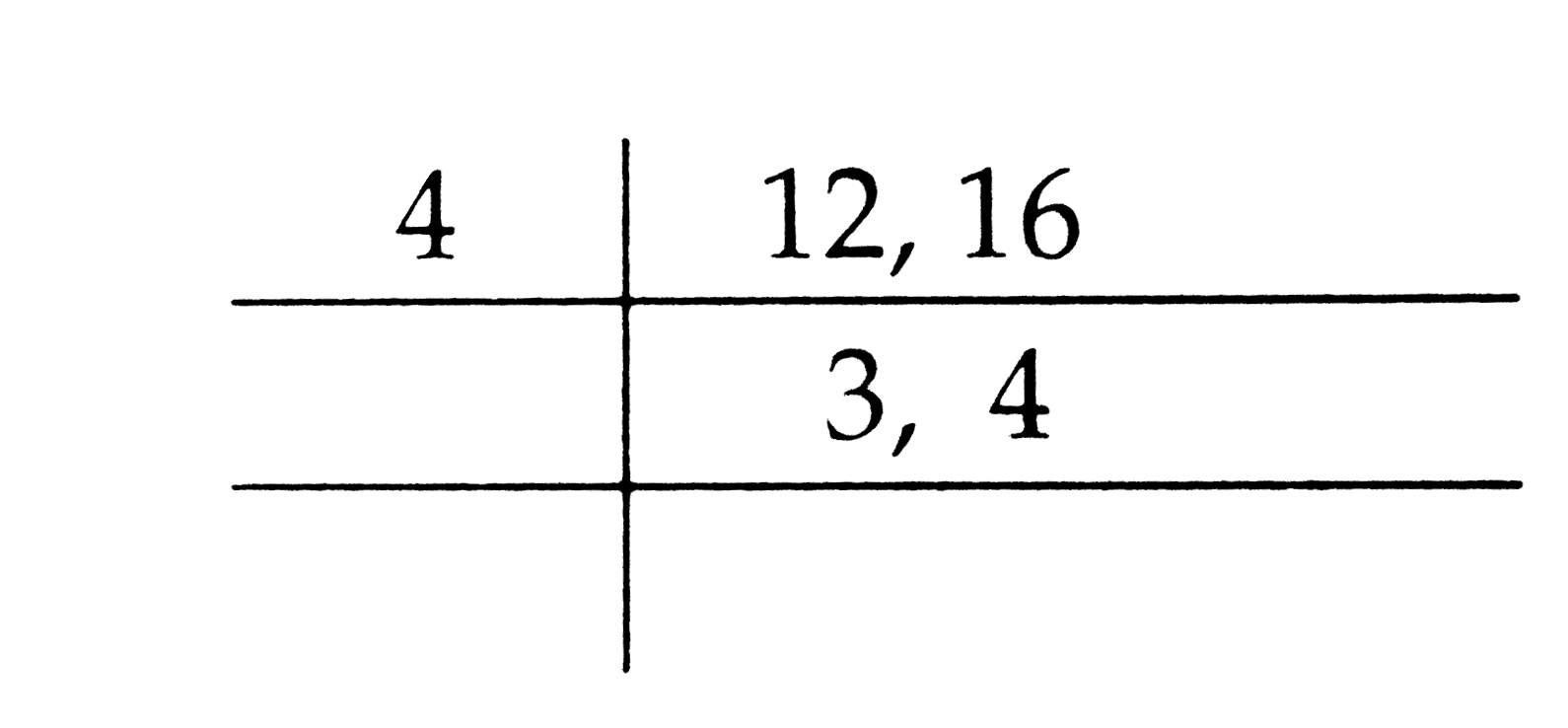
|
|
| 3072. |
The distance between the pair of parallel lines x^(2) + 4xy + 4y^(2) + 3x + 6y- 4 = 0 is |
| Answer» Answer :D | |
| 3073. |
Statement-1 : The condition on a and b for which two distinct chords of the ellipse (x^(2))/(2a^(2))+(y^(2))/(2b^(2))=1 passing through (a,-b) are bisected by theine x+y=b "is" a^(2)+6ab-7b^(2) ge0. Because: Statement-2 equationof chord of the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 whose mid point is (x_(1),y_(1)) is T=S_(1) |
|
Answer» Statement 1 is TRUE, Statement -2 is True, Statement -2 is a correct exlpanation for Statement 1 |
|
| 3074. |
The set of values of x which satisfy 5x+2 lt 3x +8 and (x+2)/(x-1) lt 4 is |
|
Answer» `(2, 3)` |
|
| 3075. |
Um A contains 7 white and 3 black balls, um B contains 4 white and 6 black balls, um C contains 2 white and 8 black balls. One of these urns is chosen at random with probabilities 0.2, 0.6 and 0.2 respectively. From the chosen urn, two balls are drawn at random without replacement. Both the balls happen to be white. Find the probability that the balls drawn are from the urn C. |
|
Answer» Let E be the event that 2 white BALLS are DRAWN. Then, `P(E//A)=(.^7C_2)/(.^10C_2),P(E//B)=(.^4C_2)/(.^10C_2),P(E//C)=(.^2C_2)/(.^10C_2)` `:.` required probability `=P(C//E)=(P(E//C).P(C))/(P(E//A).P(A)+P(E//B).P(B)+P(E//C).P(C))`. |
|
| 3076. |
If x ge 0, y ge 0, 2x+3y le 12, 3x+y le 12, then the minimum value of f=5x+7y is |
|
Answer» 0 |
|
| 3077. |
The sloope of the line touching both the parabolas y^(2) =4x and x^(2) =32yis |
|
Answer» `(1)/(2) ` |
|
| 3078. |
Integration by partial fraction : int(4e^(x)+6e^(-x))/(9e^(x)-4e^(-x))dx=Ax+B log(9e^(x)-4e^(-x))+c then A+B=. |
|
Answer» `(4)/(9)` |
|
| 3079. |
Which month had the largest percentage of vegetable sales relative to total sales? |
|
Answer» Jan |
|
| 3080. |
If x in[(4n+1)(pi)/(2),(4n+3)(pi)/(2)] and n in N, then the value of int_(0)^(x)[cos t] dt, is |
|
Answer» `(2n-1)(PI)/(2)-X` Now, `overset(x)UNDERSET(0)int [cos t]dt=overset((4n+1)pi//2)underset(0)int [cos t]dt+overset(x)underset((4n+1)pi//2)int[cos t]dt` `rArr overset(x)underset(0)int [cos t]dt=overset(2npi+pi//2)underset(0)int [cos t]x" dt"+overset(x)underset(2npi+pi//2)int [cos t]dt` 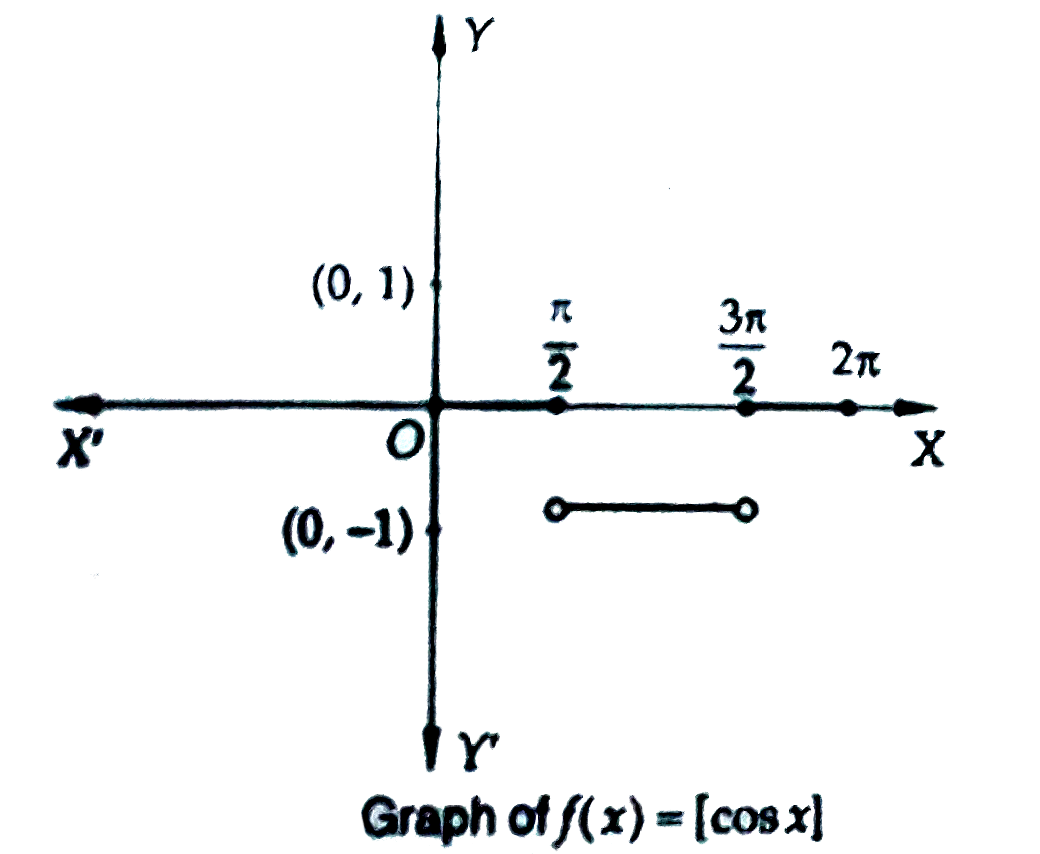 `rArr overset(x)underset(0)int [cos t]dt=overset(2npi)underset(0)int [cos t]dt+overset(2npi+pi//2)underset(2npi)int [cos t]dt+overset(x)underset(2npi+pi//2)int [cos t]dt` `rArr overset(x)underset(0)int [cos t]dt=n overset(2npi)underset(0)int[cos t]dt+overset(pi//2)underset(0)int [cos t]dt+overset(x)underset(2npi+pi//2)int[cos t]dt` `rArr overset(x)underset(0)int [cos t]dt=n[overset(pi//2)underset(0)int 0 dt+overset(3PI//2)underset(pi//2)int (-1)dt+overset(2pi)underset(3pi//2)int 0 dt]+overset(pi//2)underset(0)int 0 dt+overset(x)underset(2npi+pi//2)int -1 dt` `rArr overset(x)underset(0)int [cos t]dt=n[-((3pi)/(2)-(pi)/(2))]-[x-(2n+(pi)/(2))]` `rArroverset(x)underset(0)int [cos t]dt=npi+(pi)/(2)-x=(2n+1)(pi)/(2)-x` |
|
| 3081. |
Find value of sin^-1(cos((33pi)/5)) |
| Answer» | |
| 3082. |
If P(A)=0.3, P("not" B)=0.4,P(AintB')=0.5 and A and B are independent events, find P(A and not B) |
|
Answer» |
|
| 3084. |
Let N be the set of all natural number , Z be the set of all integers and sigma : N to Zbe difinedby{:sigma(n)={((n)/(2)",",if,n" is even"),(,,"then"),(-(n-1)/(2)",",if,n" is odd"):} |
|
Answer» `SIGMA`is ONTO not ONE-one |
|
| 3085. |
Match the following |
|
Answer» e,b,d,c |
|
| 3089. |
A,B, and C are the unequal faces of a rectanglular tank. The tank contains a certain amount of water. When the tank is based on the face A, the height of the water is half the height of the tank. The dimensions of the side B are 3 ft. xx ft, and the dimensions of side C are 4 ft xx 5 ft, what is the measure of the hight of the water in the tank in feet? |
|
Answer» 2 |
|
| 3091. |
Compute the following: [1 \ 2 \3]+ [2 \ 3 \ 4] |
| Answer» SOLUTION :`[[1,2,3]],[2,3,4]=[[2,3,4],[4,6,8],[6,9,12]]` | |
| 3092. |
a **b = a^(2)+b^(2) + ab + 2on Z then 3**4 = ...... |
|
Answer» 39 |
|
| 3093. |
Find the equation of the tagent to the curve y^(2)-2x^(3)+8=0 at the point (2,1) |
| Answer» | |
| 3096. |
The solution of x dx + ydx = x^(2)y dy - xy^(2)dx is |
|
Answer» `x^(2) - 1 = c(1+y^(3))` |
|
| 3097. |
Show that when the curved surface of a is right circular cylinder inscribed in a sphere of radius R is maximum , then the height of the cylinder is sqrt(2R). |
| Answer» Answer :C | |
| 3098. |
Between 5pm and 6pm, I looked at my watch mistaking the hour hand for the minute hand and the minute hand for the hour hand, I mistook the time to be 57 minutes earlier than the actual time. Find the number of minutes past 5 when I looked at my watch. |
|
Answer» |
|
| 3099. |
int(x^(6)+7x^(5)+6x^(4)+5x^(3)+4x^(2)+3x+1)e^(x)dx=.......+c |
|
Answer» `sum_(i=0)^(7)X^(i)E^(x)` |
|
| 3100. |
Let hat(alpha),hat(beta),hat(gamma) be three unit vectors such that hat(alpha)xx(hat(beta)xxhat(gamma)) =(1)/(2)(hat(beta)+hat(gamma))" where "hat(alpha)xx(hat(beta)xxhat(gamma))=(hat(alpha).hat(gamma))hat(beta)-(hat(alpha).hat(beta))hat(gamma). If hat(beta)" is not parallel to "hat(gamma)," then the angle between "hat(alpha)andhat(beta) is |
| Answer» Answer :D | |