A compound made of particles A and B. A forms fc c packing and B occupies all the OV_(s). If all the particles along the plane as shown in the figure below are removeed, then the simplest formula of the compound is

A compound made of particles A and B. A forms fc c packing and B occup

1.	A compound made of particles A and B. A forms fc c packing and B occupies all the OV_(s). If all the particles along the plane as shown in the figure below are removeed, then the simplest formula of the compound is
Answer» `A_(5)B_(7)` `A_(7)B_(5)` `AB` `AB_(3.75)` Solution :c. Since the lattice is `fc c (Z_(eff) = 4)`, therefore, numbered of `A` ions `= 4 (1` corner `+ 3` face centre) `(OV_(s)` are FORMED at body centre andedge centre). ltbr. Lons are removed from the plane `(PQRS)` as shown in the figure. From the figure, it is clear, `4`corner ions and two edge centre ions on `PQ` and `RS` are alos removed. Also two face centre ionslying on `PR` and `QS` along with ONE ions on present in the body centre are removed as shown in the figure below. b 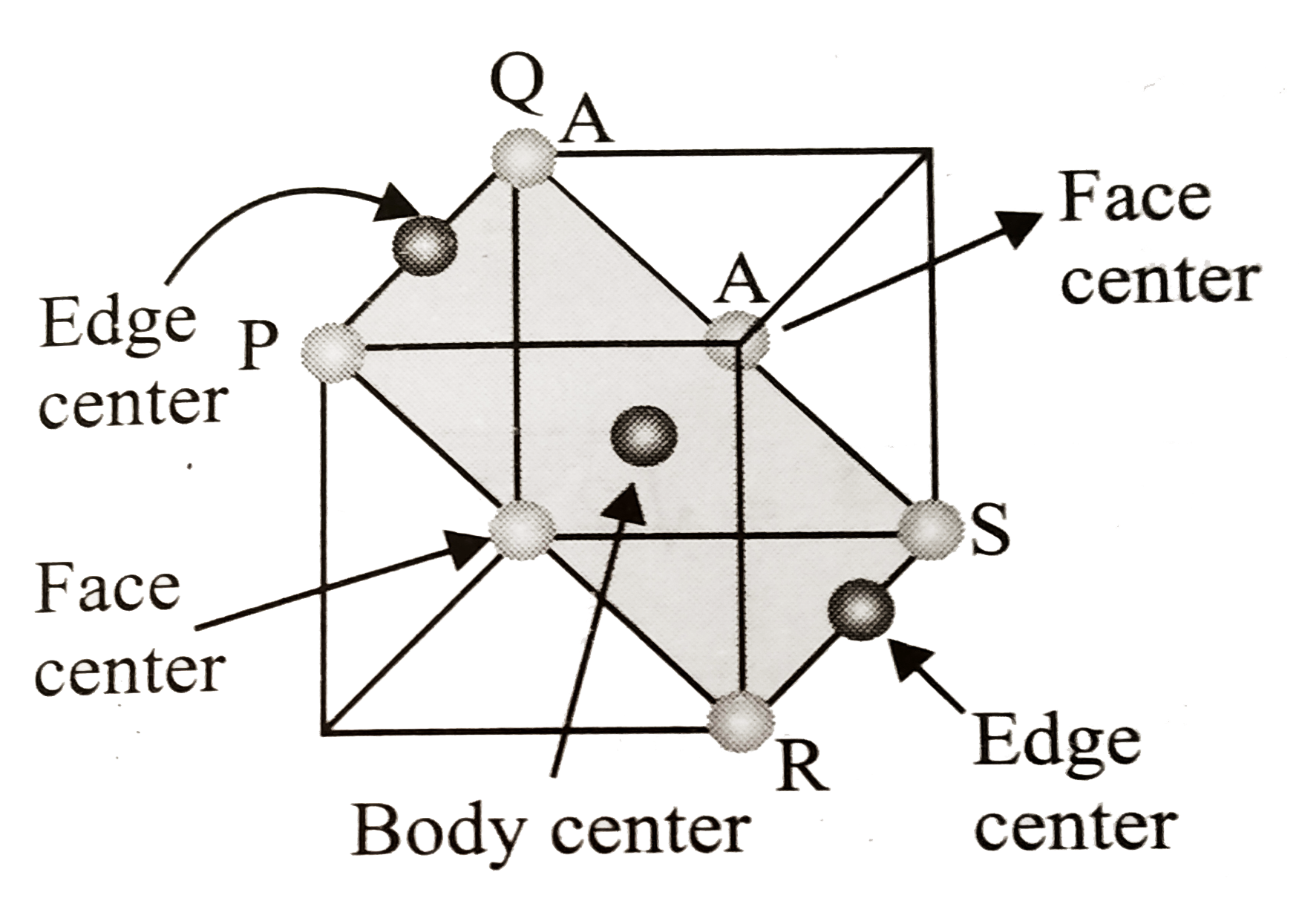`:.` Number of `A` ions removed `= 4 xx (1)/(8)` (corner SHARE) `+ 2 xx (1)/(2)` (face centre share) `= (1)/(2) + 1 = 1(1)/(2)` Number of `B` ions removed `2 xx (1)/(4)` (edge centre share) `+ (1)/(1)` (body centre share) `= (1)/(2) + 1 = 1(1)/(2)` Number of `A` ions left `= 4 -1(1)/(2) = 2.5` Number of `B` ions left `= 4 -1(1)/(2) = 2.5` Thus, formula `= A_(2.5) B_(2.5) = 2.5 AB` Simplest formula `= AB`