Saved Bookmarks
| 1. |
(a) Shown below with what angular speed 'omega' must 'm' with a radius 'r' rotate on a frictionless table so that 'M' does not move ?(b) If m=1.0kg, M=10.0 kg and r=0.5 m, find omega. |
|
Answer» SOLUTION :(a) Tension in the string = Weight of the hanging mass M. The tension in the string supplies the required CENTRIPETAL force to the body of mass m to revolve in a circular orbit of RADIUS r. 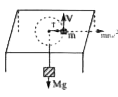 `T=mr omega^(2)` `therefore mr omega^(2)=Mg` Angular speed, `omega = SQRT((Mg)/(mr))=sqrt((10xx9.8)/(1xx0.5))=sqrt(196)=14 RAD s^(-1)`. |
|