Saved Bookmarks
| 1. |
A solution of Fe^(2+) is titrated potentiaometrically using Ce^(4+) solution . Calculate the EMF of the redox electrode thus formed when a. 50% of Fe^(2+) is titrated b. 90% of Fe^(2+) is titrated c. 110% titration is done Given :E^(c-)._(Fe^(2+)|Fe^(3+))=-0.77V and Fe^(2+)Ce^(4+)rarrFe^(3+)+Ce^(3+),K=10^(14) |
|
Answer» Solution :`a.` During titration, the REDOX electrode is `Pt|Fe^(2+),Fe^(3+)` electrode `E=E^(c-)._(cell)-(0.059)/(n)log.([Fe^(3+)])/([Fe^(2+)])` `Fe^(3+) +e^(-) RARR e^(2+)` At `50%` titration, `[Fe^(3+)]=[Fe^(2+)]` `:. E=E^(c-)=-0.77V` `b.` At `90%` titration, `([Fe^(3+)])/([Fe^(2+)])=(90)/(10)` `{:(,Fe^(2+),rarr,Fe^(3+),+e^(-)),(Initial,90,,10,),(Fi nal,10,,90,):}` `:. E=-0.77-0.059log 9 =-0.826 V` `c.` 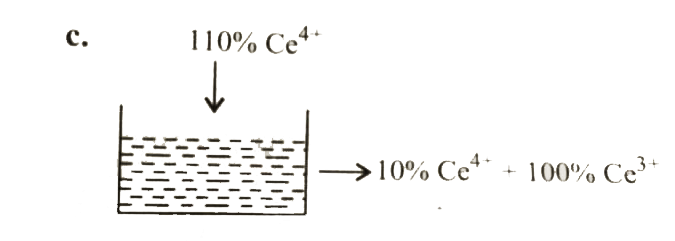 At `100%` titration, the electrode becomes, `Pt|Ce^(3+),Ce^(4+)` electrode,where`([Ce^(4+)])/([Ce^(3+)])=(10)/(100)` Cell reaction `:` 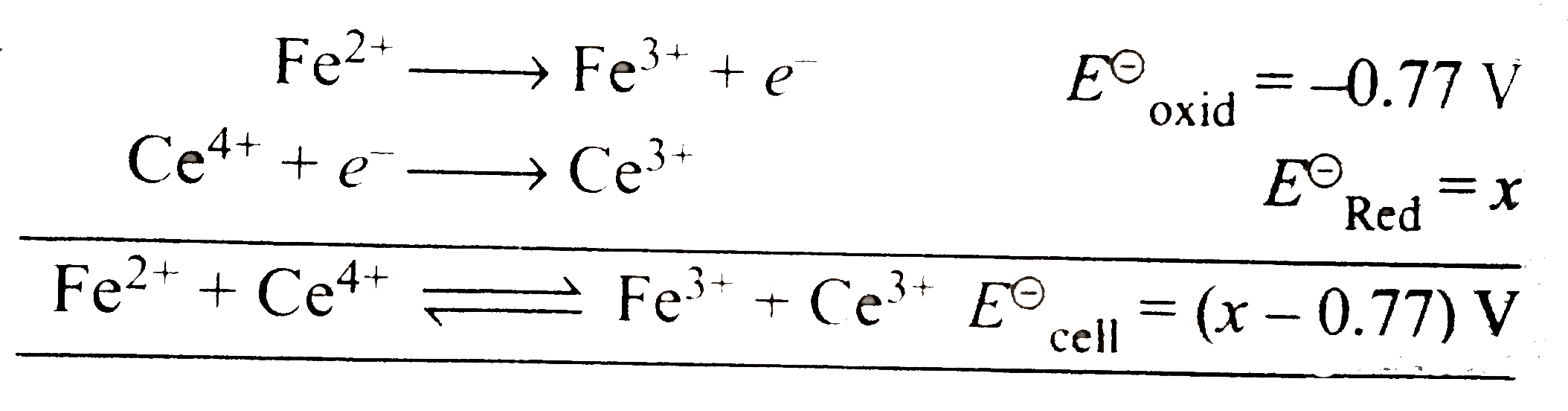 At equilibrium, `E_(cell)=0` `E=E^(c-)._(cell)-(0.059)/(1) log K ` `E^(c-)._(cell)=(0.059)/(1) log 10^(14)` `=0.826` `:. x-0.77=0.822impliesx=1.596` `:. E^(c-)._(Ce^(4+)//Ce^(3+))=1.596V` `:.E^(c-)._(Ce^(3+)//Ce^(4+))=-1.596V` So at `110%` titration, `E_(Ce^(3+)//Ce^(4+))=E^(c-)._(Ce^(3+)//Ce^(4+))-0.059log .([Ce^(4+)])/([Ce^(3+)])` `=-1.596-0.0596 log ((10)/(100))` `=-1.596+0.059=-1.537` |
|