Saved Bookmarks
| 1. |
Derive an equation for solution which shows relation between total pressure and mole fraction of volatile solute and volatile solvent and explain it by plotting graph. |
|
Answer» Solution :Suppose in a binary meaning volatile solution component 1 and component 2 is present. Their mole fraction is `X_(1)` and `X_(2)` and their vapour pressure is `p_(1)` and `p_(2)` respective. According to the Raoult.s law, a solution of volatile liquids, the PARTIAL vapour pressure of each component of the solution is directl proportional to its mole fraction present in solution. Thus, for componnent 1 , `p_(1)prop X_(1)` and `p_(1)=p_(1)^(0). X_(1)` where `p_(1)` is the vapour pressure of pure component 1 at the same temperature. Similarly, for component 2, `p_(2) prop X_(2)`and`p_(2)=p_(2)^(0).X_(2)`, where `p_(2)^(0)` represents the vapour pressure of the pure component 2. According to Dalton.s law of partial pressures, the total pressure (total p) over the solution phase in the container will be the sum of the partial pressures of the components of the solution. `p_("total")=p_(1)+p_(2)` `p_("total")=p_(1)^(0).x_(1)+p_(2)^(0).x_(2)` `=(1-x_(2))p_(1)^(0)+x_(2)p_(2)^(0)` `p_("total")=p_(1)^(0)+x_(2)(p_(2)^(0)-p_(1)^(0))` Following conclusions can be drawn from equation : (i) Total vapour pressure over the solution can be related to the mole fraction of any one component. (ii) Total vapour pressure over the solution VARIES linearly with the mole fraction of component 2. (iii)Depending on the vapour pressures of the pure components 1 and 2, total vapour pressure over the solution decreases or increases with the increase of the mole fraction of component 1. A plot of `p_(1)` or `p_(2)` versus the mole fractions `X_(1)` and `X_(2)` for a solution given a linear plot as shown in figure. 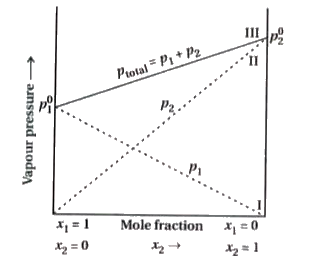 These lines (I and II) pass through the points for which `X_(1)` and `X_(2)` are EQUAL to unity. Similarly the plot (line III) of `p_("total")` versus `X_(2)` is also linear. The minimum value of `p_("total")` is `p_(1)^(0)` and the maximum value is `p_(2)^(0)`, assuming that component 1 is less volatile than component 2, i.e., `p_(1)^(0)lt p_(2)^(0)`. The COMPOSITION of vapour phase in equilibrium with the solution is determined by the partial presures of the components. If `Y_(1)` and `Y_(2)` are the mole fractions of the components 1 and 2 respectively in the vapour phase than, using Dalton.s law of partial pressures: `p_(1)=Y_(1)p_("total")` and `p_(2)=Y_(2)p_("total")` So, in general `p_(i)=Y_(i)p_("total")` |
|